
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические указания. Для выполнения данного задания внимательно изучите приведенные ниже примеры с подробными решениями, а затем выполните аналогичные практические задания
|
|
Для выполнения данного задания внимательно изучите приведенные ниже примеры с подробными решениями, а затем выполните аналогичные практические задания.
ПРИМЕР 1:. Найти решение дифференциальных уравнений с разделяющимися переменными 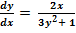 . Решение: Произведём разделение переменных: (3y2 + 1)dy = 2xdx.Проинтегрируем левую и правую часть. 3
. Решение: Произведём разделение переменных: (3y2 + 1)dy = 2xdx.Проинтегрируем левую и правую часть. 3 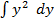 +
+  = 2
= 2 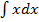 .3
.3 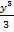 + y + C = 2
+ y + C = 2 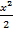 , y3 + y + C = x2, или x =
, y3 + y + C = x2, или x = 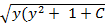 .3yy' = x. Запишем уравнение в виде: 3y
.3yy' = x. Запишем уравнение в виде: 3y  = x и произведём замену переменных: 3ydy = xdx, тогда 3
= x и произведём замену переменных: 3ydy = xdx, тогда 3 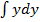 =
= 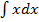 3
3 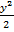 =
= 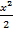 + C/2 или 3y2 = x2 + C, тогда y =
+ C/2 или 3y2 = x2 + C, тогда y =  .
.
ПРИМЕР 2:
Найти решение однородных дифференциальных уравнений первого порядка
(2x – y)dx + (2y – x)dy = 0. Разрешим уравнение относительно dy/dx:
y' = 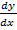 = -
= - 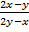 , поделив числитель и знаменатель правой части на х, получим:
, поделив числитель и знаменатель правой части на х, получим:
y' = -  , т. е. у' есть функция отношения у/х. Это означает, что данное уравнение однородное. Для решения этого уравнения введём новую функцию u = y/x. Тогда у = ux, y' = xdu/dx + u. Исходное уравнение запишется в виде уравнения с разделяющимися переменными:
, т. е. у' есть функция отношения у/х. Это означает, что данное уравнение однородное. Для решения этого уравнения введём новую функцию u = y/x. Тогда у = ux, y' = xdu/dx + u. Исходное уравнение запишется в виде уравнения с разделяющимися переменными:
x 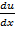 + u =
+ u = 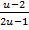 ; x
; x 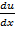 =
= 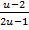 - u =
- u = 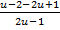 =
= 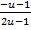 ,
, 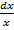 = -
= - 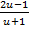 du =
du = 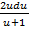 -
- 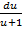 . Проинтегрируем это уравнение:
. Проинтегрируем это уравнение:
ln 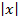 = 2
= 2 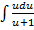 -
- 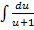 + lnC.
+ lnC.
ln  = 2(u – ln(u + 1)) – ln(u + 1) = 2u – l-2ln(u + 1) – ln(u + 1) = 2u – 3 ln(u + 1),
= 2(u – ln(u + 1)) – ln(u + 1) = 2u – l-2ln(u + 1) – ln(u + 1) = 2u – 3 ln(u + 1),
ln  + ln(u + 1)3 = 2u, ln
+ ln(u + 1)3 = 2u, ln  (u + 1)3 = 2u,
(u + 1)3 = 2u,  (u + 1)3 = e2u, и окончательно получаем решение:
(u + 1)3 = e2u, и окончательно получаем решение:  (
( + 1)3 = exp (
+ 1)3 = exp (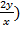 . xdy – ydx = ydy, (x – y)dy = ydx y
. xdy – ydx = ydy, (x – y)dy = ydx y  =
=  .
.
Для решения этого уравнения введём новую функцию u = y/x. Тогда у = ux, y' = xdu/dx + u. Исходное уравнение запишется в виде уравнения с разделяющимися переменными:
x 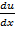 + u =
+ u = 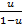 ; x
; x 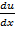 =
= 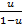 - u =
- u = 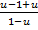 =
=  ,
, 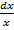 = -
= - 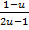 du =
du = 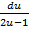 -
-  . Проинтегрируем это уравнение:
. Проинтегрируем это уравнение:
ln 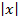 =
= 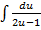 -
-  + lnC, ln
+ lnC, ln  = ln(2u - 1) – u - ln(2u – 1) = - u, окончательно получаем:
= ln(2u - 1) – u - ln(2u – 1) = - u, окончательно получаем:
x = Ce-u = Ce-y/x.
ПРИМЕР 3:. Найти решение линейных дифференциальных уравнений первого порядка
y  - y ctg x = 2x sin x. Положим y = uv, тогда y' = u'v + uv' и данное уравнение принимает вид: u'v + uv' - uv ctg x = 2x sin x, u'v + u(v' – v ctg x) = 2x sin x.
- y ctg x = 2x sin x. Положим y = uv, тогда y' = u'v + uv' и данное уравнение принимает вид: u'v + uv' - uv ctg x = 2x sin x, u'v + u(v' – v ctg x) = 2x sin x.
Решая уравнение v' – v ctg x = 0, получим его простейшее частное решение:
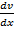 = v ctg x;
= v ctg x; 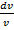 = ctg x dx; ln
= ctg x dx; ln 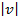 = ln
= ln  ; откуда v = sin x.
; откуда v = sin x.
Подставляя v в исходное уравнение получаем уравнение: u  sin x = 2x sin x, из которого находим u u' = 2x, следовательно du = 2xdx u = x2 +C.
sin x = 2x sin x, из которого находим u u' = 2x, следовательно du = 2xdx u = x2 +C.
Итак, искомое решение y = (x2 + C) sin x, y' + 3y tg 3x = sin 6x, y(0) = 1/3.
Положим y = uv, тогда y' = u'v + uv' и данное уравнение принимает вид:
u'v + uv' + 3uv tg 3x = sin 6x, u'v + u(v' + 3v tg 3x) = sin 6x.
Решая уравнение v' + 3v tg 3x = 0, получим его простейшее частное решение:
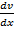 = 3v tg x;
= 3v tg x; 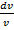 = 3tg 3x dx; ln
= 3tg 3x dx; ln 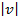 = - ln
= - ln  ; откуда v = 1/cos 3x.Подставляя v в исходное уравнение получаем уравнение: u
; откуда v = 1/cos 3x.Подставляя v в исходное уравнение получаем уравнение: u  /cos 3x = sin 6x, из которого находим u
/cos 3x = sin 6x, из которого находим u
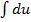 =
= 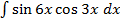 , u = -
, u = - 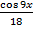 –
–  + C, и окончательно получим решение
+ C, и окончательно получим решение
y = uv = -  (
( + C). Найдём постоянную С, согласно заданным начальным условиям у(0) = 1/3, 1/3 = -
+ C). Найдём постоянную С, согласно заданным начальным условиям у(0) = 1/3, 1/3 = - 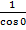 (
( + C) = - 4/18 - C, C = - 1/3 - 4/18 = - 10/18 = - 5/9. Получаем решение:
+ C) = - 4/18 - C, C = - 1/3 - 4/18 = - 10/18 = - 5/9. Получаем решение:
у = -  (
( - 5/9) = -
- 5/9) = -  (
(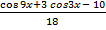 ) = -
) = -  .
.
ПРИМЕР 4: Проинтегрировать следующие линейные неоднородные уравнения
y'' + y' – 6y = 0
Запишем характеристическое уравнение. Для этого заменим функцию у и её производные соответствующими степенями λ: λ2 + λ - 6 = 0
откуда λ1 = - 3 и λ2 = 2. Так как корни характеристического уравнения действительные и различные, то общее решение данного дифференциального уравнения имеет вид:
у = С1е-3х + С2е2х.
ПРИМЕР 5: Найти общее решение уравнения однородного уравнения: у'' + 2у' + 5y = 0.
Решая отвечающее ему характеристическое уравнение λ2 + 2λ + 5 = 0, получаем комплексные корни λ1 = - 1 – 2i; λ2 = - 1 + 2i, следовательно, у = e-х(C1 cos x + C2 sin 2x).
Форма отчетности
Выполненные задания оформить по одному из трёх вариантов:
1) Напечатать в программе MICROSOFT WORD (кегль - 14, интервал – 1,5; шрифт - Times New Roman; поля – 1,2,1,1; нумерация страниц). Сохранить файл под своей фамилией и сдать электронную версию преподавателю на носителе. Распечатать на листах формата А4.
2) Письменно на листах формата А4, с одной стороны, ручкой синего или чёрного цвета.
3) Обычный текст распечатать на листах формата А4, а математический текст и рисунки письменно от руки также на листах А4.
Во всех трех вариантах оформить титульный лист (Приложение 1), работу вложить в файл и сдать в назначенный срок.
Рекомендуемая литература:
1. Баврин И.И. Высшая математика.- М.: АСАDEMA,2008.
2. Богомолов Н.В. Практические занятия по математике: Учебное пособие, 10-е изд. – М.: Высшая школа, 2008.
3. Валуцэ И.И. Математика для техникумов. - М.: Наука,2008.
4. Выгодский М.Я. Справочник по высшей математике. – М.: Рост книга, 2009.
5. Гмурман В.Е. Теория вероятностей и математическая статистика.-М.: Высшая школа, 2008.
6. С.Г. Григорьев, С.В.Задулина. Математика.-М.: АСАDEMA,2008.
7. Дадаян А.А. Сборник задач по математике.-М.: ФОРУМ-ИНФРА-М,2009.
8. Дадаян А.А. Математика.-М.: ФОРУМ-ИНФРА-М,2009.
9. Натансон И.П. Краткий курс высшей математики. – С-Пб.: Лань, 2010.
10. Щипачев В.С. Основы высшей математики. – М.: В.Ш., 2009.
11. Щипачев В.С. Задачи по высшей математике. - М.: В.Ш., 2008.
12. INTERNET
Критерии оценивания работы:
Каждое выполненное задание теоретического и практического блоков самостоятельной работы оценивается в баллах по 5-бальной системе. Учитывается полнота выполнения и объём, грамотность, научность, последовательность и аккуратность оформления. Затем выставляется общая (усреднённая) оценка за всю работу в целом. Максимальное количество баллов по данной работе 10. Итоговая оценка за работу: «5»- 10 баллов, «4» - (7-9) баллов, «3» - (5-6) баллов. Оценка выставляется в журнал для учёта самостоятельных работ. Каждая работа должна быть сдана в строго установленные строки, в противном случае преподаватель имеет право снизить оценку, а при её невыполнении поставить неудовлетворительную оценку.
Приложение 1
Дисциплина: МАТЕМАТИКА
Date: 2015-09-24; view: 574; Нарушение авторских прав