
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические указания. Для выполнения данного задания нужно знать формулы производных; область определения и значения функции; точки разрыва
|
|
Для выполнения данного задания нужно знать формулы производных; область определения и значения функции; точки разрыва, перегиба, экстремума; интервалы возрастания и убывания функции, асимптоты.
Разобранный материал теоретический материал из задания№1 будет служить основой для выполнения практических заданий. Обратите внимание на приведенный ниже разобранные примеры.
Пример 1: Исследовать функцию ƒ(х)=х3-3х-4 на возрастание и убывание.
Решение: Функция определена на R=(- ∞; ∞). Ее производная равна: ƒ'(х)=3х2-3=3(х-1)(х+1); ƒ'(х)>0 при х є (- ∞;-1)U(1; ∞); ƒ'(х)<0 при хє (-1;1).
Ответ: данная функция возрастает на интервалах (- ∞;-1) и (1; ∞); убывает на интервале (-1;1).
Пример 2: Исследовать функцию и построить ее график.
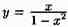
Решение:
1. Функция не определена при х=1и х=-1. Область ее определения состоит из трех интервалов (-∞;-1), (-1;1), (1;+∞), а график из трех ветвей.
2. Если х=0, тоу=0. График пересекает ось Оу в точке О(0;0); если у=0, то х=0. График пересекает ось Ох в точке О(0;0).
3. Функция знакоположительна (у>0) в интервалах (-∞;-1) и (0;1); знакоотрицательна — в (-1;0) и (1;+∞).
4. Функция 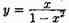 является нечетной, т. к.
является нечетной, т. к.

Следовательно, график ее симметричен относительно начала координат. Для построения графика достаточно исследовать ее при х≥0.
5. Прямые х=1 и х=-1 являются ее вертикальными асимптотами. Выясним наличие наклонной асимптоты:
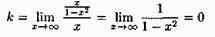
(k=0 при х→+∞ и при х→-∞),

Следовательно, есть горизонтальная асимптота, ее уравнение у=0. Прямая у=0 является асимптотой и при х → +оо, и при х → —со.
6. Находим интервалы возрастания и убывания функции. Так как
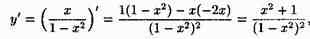
то у'>0 в области определения, и функция является возрастающей на каждом интервале области определения.
7. Исследуем функцию на экстремум. Так как
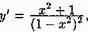
то критическими точками являются точки x1=1 и х2=-1 (у' не существует), но они не принадлежат области определения функции. Функция экстремумов не имеет.
8. Исследуем функцию на выпуклость. Находим у":


Вторая производная равна нулю или не существует в точках х1=0, х2=-1, х3=1. На рисунке представлена схема изменения знаков второй производной исследуемой функции.
Точка О(0,0) — точка перегиба графика функции.
График выпуклый вверх на интервалах (-1;0) и (1;∞); выпуклый вниз на интервалах (-∞;-1) и (0;1).
График функции изображен на рисунке.

Форма отчетности
Выполненные задания оформить по одному из трёх вариантов:
1) Напечатать в программе MICROSOFT WORD (кегль - 14, интервал – 1,5; шрифт - Times New Roman; поля – 1,2,1,1; нумерация страниц). Сохранить файл под своей фамилией и сдать электронную версию преподавателю на носителе. Распечатать на листах формата А4.
2) Письменно на листах формата А4, с одной стороны, ручкой синего или чёрного цвета.
3) Обычный текст распечатать на листах формата А4, а математический текст и рисунки письменно от руки также на листах А4.
Во всех трех вариантах оформить титульный лист (Приложение 1), работу вложить в файл и сдать в назначенный срок.
Рекомендуемая литература:
1. Баврин И.И. Высшая математика.- М.: АСАDEMA,2008.
2. Богомолов Н.В. Практические занятия по математике: Учебное пособие, 10-е изд. – М.: Высшая школа, 2008.
3. Валуцэ И.И. Математика для техникумов. - М.: Наука,2008.
4. Выгодский М.Я. Справочник по высшей математике. – М.: Рост книга, 2009.
5. Гмурман В.Е. Теория вероятностей и математическая статистика.-М.: Высшая школа, 2008.
6. С.Г. Григорьев, С.В.Задулина. Математика.-М.: АСАDEMA,2008.
7. Дадаян А.А. Сборник задач по математике.-М.: ФОРУМ-ИНФРА-М,2009.
8. Дадаян А.А. Математика.-М.: ФОРУМ-ИНФРА-М,2009.
9. Натансон И.П. Краткий курс высшей математики. – С-Пб.: Лань, 2010.
10. Щипачев В.С. Основы высшей математики. – М.: В.Ш., 2009.
11. Щипачев В.С. Задачи по высшей математике. - М.: В.Ш., 2008.
12. INTERNET
Критерии оценивания работы:
Каждое выполненное задание теоретического и практического блоков самостоятельной работы оценивается в баллах по 5-бальной системе. Учитывается полнота выполнения и объём, грамотность, научность, последовательность и аккуратность оформления. Затем выставляется общая (усреднённая) оценка за всю работу в целом. Максимальное количество баллов по данной работе 10. Итоговая оценка за работу: «5»- 10 баллов, «4» - (7-9) баллов, «3» - (5-6) баллов. Оценка выставляется в журнал для учёта самостоятельных работ. Каждая работа должна быть сдана в строго установленные строки, в противном случае преподаватель имеет право снизить оценку, а при её невыполнении поставить неудовлетворительную оценку.
Приложение 1
Дисциплина: МАТЕМАТИКА
Date: 2015-09-24; view: 311; Нарушение авторских прав