Решение задач

по учебной дисциплине

«Теоретические Основы Управления»

Выполнил: магистрант группы МЭЭ-01-13/03

Нестерин Андрей Алексеевич

Проверил: доцент, к. т. н.

Мочалов Михаил Юрьевич

Чебоксары 2014 г.

1) Определить передаточную функцию в операторной форме системы управления, которая описываются следующим уравнением:

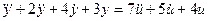
Передаточная функция в операторной форме будет иметь следующий вид:

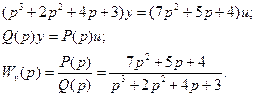
2) Записать дифференциальное уравнение системы управления, передаточная функция которой имеет следующий вид:

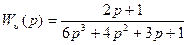
Дифференциальное уравнение системы имеет вид:

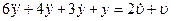
3) Определить весовую и переходную функции для звена со следующей передаточной функцией:

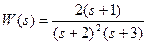
Из определения переходной функции следует, что 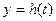при 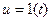. Так как при этом 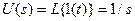и 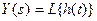, то получаем

.

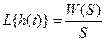Переходная функция по теореме разложения:

.

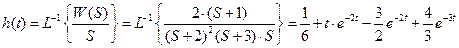Весовая функция:

.

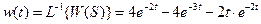4) Определить частотную передаточную функцию, вещественную, мнимую, амплитудную, фазовую, логарифмическую амплитудную частотные функции, переходную и весовую функции апериодического звена.

Апериодическое звено

.

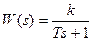Его частотные и временные функции:

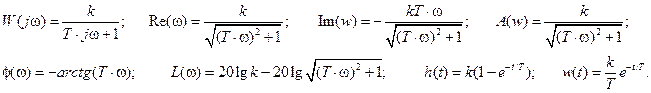
5) На вход системы подается сигнал u = 2×sin(0.5t). Определить в установившемся режиме реакцию системы со следующей передаточной функцией:

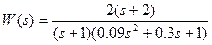
Изображение входного сигнала

.

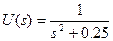Изображение выходного сигнала

.

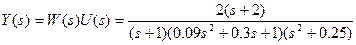Установившееся значение оригинала:

.

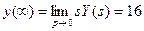6) Построить асимптотическую ЛАЧХ звена со следующей передаточной функцией:

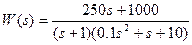
Преобразование:

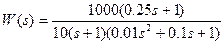
Для построения ЛАЧХ (рисунки 1,2) последовательного соединения звеньев следует построить соответствующие характеристики каждого звена, и затем геометрически их сложить:

a. Пропорциональное звено: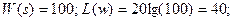

b. Форсирующее звено: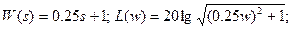

c. Апериодическое звено: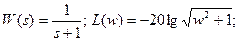

d. Колебательное звено: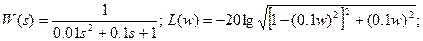

7) Записать передаточные функции звеньев, если их асимптотические ЛАЧХ имеют следующий вид:

7)

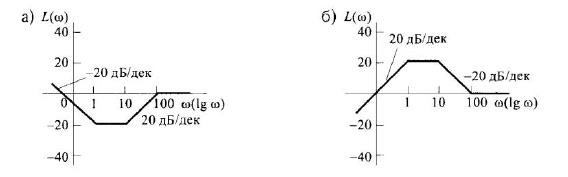
a) ;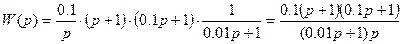

b) .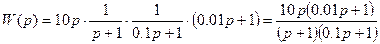

Рисунок 1 – Асимптотическая ЛАЧХ

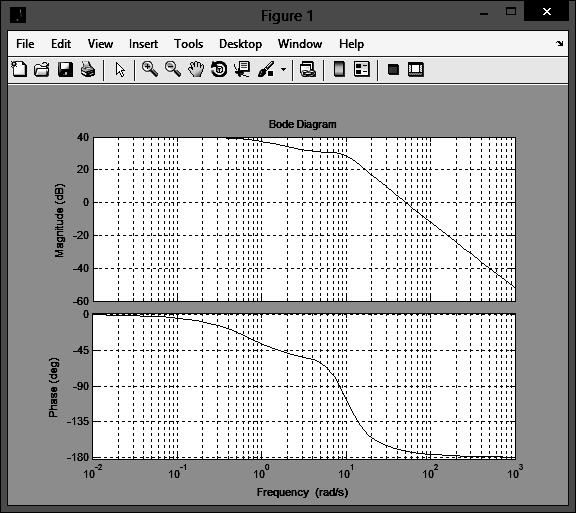
Рисунок 2 – ЛАЧХ

8) Для системы на рисунке определить следующие передаточные функции (ПФ):

а) Wyg — ПФ относительно входа g и выхода у,

б) Wyf — ПФ относительно входа f и выхода y.

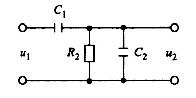
9) Составить передаточную функцию для пассивного четырехполюсника, показанного на рисунке:

C1 = 4 мкФ, R2 = 200 кОм, С2 = 1 мкФ.

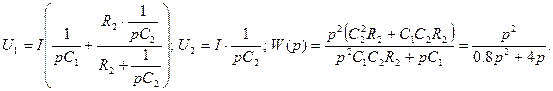
10) Исследовать устойчивость системы управления, у которой характеристическое уравнение имеет следующий вид:

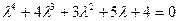
Корни характеристического уравнения:

p₁=-3.4534; p₂=0.15032 + 1.1595i;

p₃=0.15032 - 1.1595i; p₄=-0.84722.

Система неустойчива.

11) Исследовать устойчивость системы управления, которая описывается следующим уравнением:

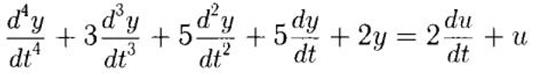
Характеристическое уравнение:

.

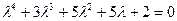Корни характеристического уравнения:

p₁= -0.5 + 1.3229i; p₂= -0.5 - 1.3229i;

p₃= -1; б p₄= -1.

Система устойчива.

12) Исследовать устойчивость замкнутой системы при следующей передаточной функции разомкнутой системы:

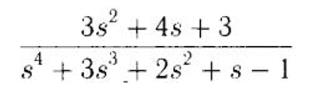
Характеристическое уравнение:

.

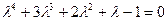Корни характеристического уравнения:

p₁= -2.4142; p₂= -0.5 + 0.86603i;

p₃= -0.5 - 0.86603i; p₄= 0.41421.

Система неустойчива.

13) Пользуясь критерием Найквиста исследовать устойчивость замкнутой системы, если передаточная функция разомкнутой системы имеет вид:

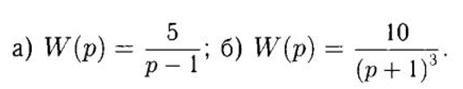
a. Система имеет один правый нуль и АФЧХ (рисунок 3) 0,5 раз охватывает точку (-1; j0). Система устойчива.

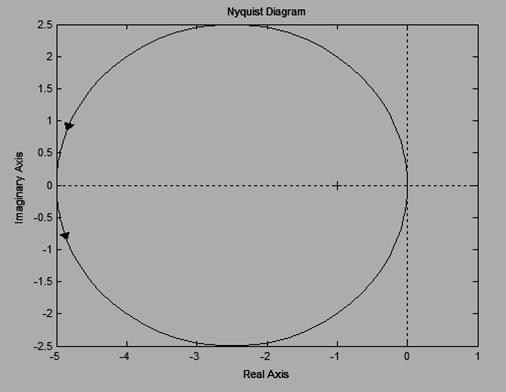
Рисунок 3 – АФЧХ для варианта а)

b. Система имеет один правый нуль и АФЧХ (рисунок 4) 1 раз охватывает точку (-1; j0). Система неустойчива.

14) Передаточная функция разомкнутой системы W(p) = k/(Тр+ 1)³. Определить область устойчивости замкнутой системы на плоскости параметров (к,Т).

Характеристическое уравнение замкнутой системы:

.

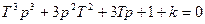Система устойчива при T>0 и k>0, а также .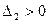

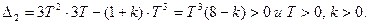
Область устойчивости:

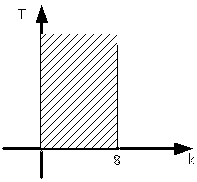
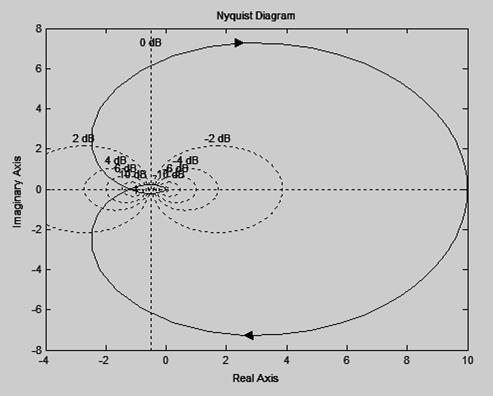
Рисунок 4 – АФЧХ для варианта б)

15) Найти уравнение кривой, представляющей собой амплитудно-фазовую характеристику дифференцирующего звена, изображенного на рисунке. Построить амплитудно-фазовую характеристику звена для случая R1 = 40 кОм, R2 = 10 кОм, С = 2,5 мкф.

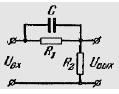
Уравнение АФЧХ:

.

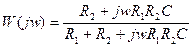АФЧХ цепи построена на рисунке 5.

16) Система автоматического управления имеет характеристическое уравнение четвертого порядка. Кривая Михайлова системы приведена на рисунке. Определить устойчивость автоматической системы.

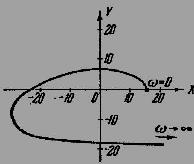
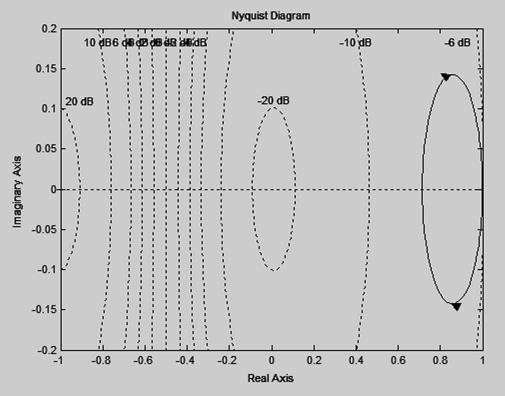
Рисунок 5 – АФЧХ дифференцирующего звена

Система устойчива.

17) Система автоматического управления имеет характеристическое уравнение пятого порядка. На рисунке приведена кривая Михайлова системы. Определить число корней характеристического уравнения с отрицательной вещественной частью и число корней характеристического уравнения с положительной вещественной частью.

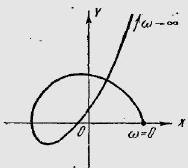
2 корня с отрицательной вещественной частью и 1 корень с положительной вещественной частью.