Модели экономического роста

Модель экономического роста, разработанная в 1928 г. американским экономистом П. Дугласом совместно с математиком Ч. Коббом, раскрывает функциональную зависимость между национальным производством (объемом продукции) и двумя независимыми, но взаимосвязанными переменными ¾ затратами капитала и труда.

Эта модель была составлена на основе изучения данных за 24 года (1899-1922) в обрабатывающей промышленности США. Предполагалось, что объем продукции является функцией только двух факторов ¾ капитала и труда (взаимосвязанных и взаимозаменяемых), что это однородная функция первой степени, т. е. увеличение каждого из факторов в п раз увеличивает функцию во столько же раз. В связи с этим можно утверждать, что: 1) эффективностьпроизводственных факторов не зависит от масштабов производства и 2) производительность труда и отдача капитала в этот период постоянны. Отсюда, они предложили следующее уравнение:

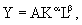
где Y ¾ объем продукции;

К¾капитал;

L ¾ труд;

a, b ¾ коэффициенты эластичности (параметры функции);

А¾ коэффициент пропорциональности, или масштабности.

Параметры, характеризующие влияние труда и капитала на объем продукции, были определены методом наименьших квадратов. В результате расчета было установлено, что за исследуемый период значение Аравно 1,01; а = ¹/₄; (3 = ³/₄. Отсюда конкретный вид функции:

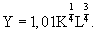
Данная функция показывает, что при изменении величины рабочей силы на 1% объем продукции изменится на 0,75%, или ³/₄, а при изменении капитала на 1% она изменится на 0,25%, или ¹/₄ (при прочих постоянных условиях). Это означает: 1) если a + b = 1, то пропорциональному приросту рабочей силы и капитала соответствует и пропорциональный прирост продукции. Иначе говоря, если оба фактора возрастают на 1%, то и прирост продукции возрастает на 1%. Эта предпосылка линейной однородности функции означает независимость эффективности от масштабов производства;

2) если же a + b > 1 или < 1; то это означает, что произошло повышение или понижение эффективности факторов вследствие изменения масштабов самого производства.

Модель А. Тинбергена. Дальнейшее развитие этой функции пошло в направлении введения фактора, отражающего научно-технический прогресс. Впервые это сделал голландский экономист А. Тинберген, введя в модель Кобба-Дугласа дополнительный множитель е ⁿ. Производственная функция приняла вид:

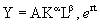
где rt¾ темп роста производства в результате НТП.

Именно этот тип производственной функции получил широкое распространение в экономической науке и практике. Ее назначение состоит в том, чтобы доказать справедливость существующего распределения национального дохода: одну часть национального дохода «вменяют» труду, другую часть ¾ капиталу, третью ¾ техническому прогрессу.

Однако не следует забывать, что макроэкономические модели могут дать лишь количественную оценку экономических взаимосвязей, но не могут полностью отразить социальные изменения, которые не поддаются непосредственной количественной оценке. Поэтому анализ экономического развития на базе производственных функций должен быть дополнен другими методами ¾ социальными.

Известны и другие модели экономического роста. Модель Харрода - Домара описывает динамику дохода. Доход Y(t)рассматривается как сумма потребления C(t)и инвестиций I(t).Экономика считается закрытой, поэтому чистый экспорт равен нулю, а государственные расходы в модели не выделяются. Основная предпосылка модели роста ¾ взаимосвязь между инвестициями и скоростью роста дохода.

Предполагается, что скорость роста дохода пропорциональна инвестициям:

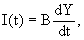
где В ¾ коэффициент капиталоемкости прироста дохода.

В модель включаются следующие предпосылки:

1) инвестиционный лаг равен нулю, т. е. инвестиции мгновенно переходят в прирост капитала. Формально это означает, что АК(t) = l(t),где AK(t)¾ непрерывная функция прироста капитала во времени;

2) выбытие капитала отсутствует;

3) производственная функция в модели линейна: это вытекает из пропорциональности прироста дохода приросту капитала:

dY(t) = -dK(t)dt - В.

Линейная производственная функция имеет следующий вид:

Y(t) = aL(t) + bK(t) + c, где b = ¹/_В.

Перечисленные предпосылки, конечно, существенно огрубляют описание динамики реальных макроэкономических процессов, делают затруднительным применение данной модели, например, для непосредственного расчета или прогноза величины совокупного выпуска или дохода. Однако данная модель и не предназначена для этого, в то же время ее относительная простота позволяет более глубоко изучить взаимосвязь динамики инвестиций и роста выпуска, получить точные формулы траекторий рассматриваемых параметров при сделанных предпосылках.

Зависимость, связывающая между собой во времени показатели инвестиций и уровень выпуска (дохода), является базовой во всех моделях макроэкономической динамики. Кроме того, в этих моделях необходимо определить принципы формирования структуры выпуска (дохода), распределения его между составляющими, прежде всего ¾ между потреблением и сбережением (накоплением).

Эти принципы могут основываться на оптимизационном подходе (обычно это максимизация совокупных объемов потребления в той или иной форме), экстраполяционном, равновесном и др. В рассматриваемой модели предполагается, что динамика объема потребления C(t)задается экзогенно. Этот показатель может считаться постоянным во времени, расти с заданным постоянным темпом или иметь какую-либо другую динамику.

Модель Р. Солоу. В его модели считаются постоянными норма сбережений и норма выбытия капитала, инвестиционные лаги отсутствуют, а производственная функция имеет постоянную отдачу от масштаба. Кроме того, на начальном уровне анализа модели ищутся не траектории изменения всех ее показателей (как в модели Харрода-Домара), а характеристики состояний устойчивого равновесия, к которым система выходит в долгосрочном периоде. С формальной точки зрения это представляет собой существенно более простую задачу.

В заключение можно сказать, что отправным пунктом в современных экономических моделях является воздействие на экономическое развитиеНТП. Научно-технический прогресс является важным фактором экономического роста. По существу, он является двигателем экономического прогресса. Скорость внедрения технических изобретений и обновления капитала во многом зависит от соотношения цены капитального оборудования и заработной платы рабочих, труд которых замещает этот капитал. На протяжении последних 50 лет в развитых странах заработная плата, как правило, росла сравнительно быстрее издержек, связанных с приобретением оборудования. Предприятия замещали труд капиталом и темпы технического прогресса заметно ускорились во многих отраслях, что на своих рабочих местах почувствовали и сельскохозяйственный рабочий, и грузчик, и транспортный рабочий, и докер, и шахтер.

НТП означает не только совершенно новое оборудование, но также и новые формы управления и организации производства, т. е. все то, что позволяет по-новому комбинировать ресурсы с целью увеличения конечного выпуска продукции.

Заметим, что все вышерассмотренные модели имеют практическое значение.

Кроме НТП большую роль в экономическом росте играет государство.

Рекомендация:

Date: 2015-09-22; view: 449; Нарушение авторских прав