Подставляем полученное соотношение в исходное уравнение

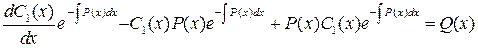
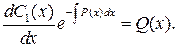
Из этого уравнения определим переменную функцию С ₁(х):

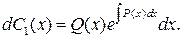
Интегрируя, получаем:

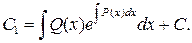
Подставляя это значение в исходное уравнение, получаем:

.

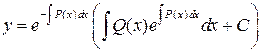Таким образом, мы получили результат, полностью совпадающий с результатом расчета по методу Бернулли.

При выборе метода решения линейных дифференциальных уравнений следует руководствоваться простотой интегрирования функций, входящих в исходный интеграл.

1.6. Уравнение Бернулли. Уравнением Бернулли называется уравнение вида

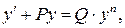
где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.

Для решения уравнения Бернулли применяют подстановку , с помощью которой, уравнение Бернулли приводится к линейному.

Для этого разделим исходное уравнение на yⁿ.

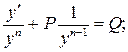
Применим подстановку, учтя, что

.

,

.

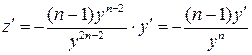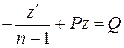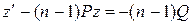Получилось линейное уравнение относительно неизвестной функции z.

Решение этого уравнения будем искать в виде:

;

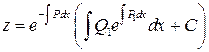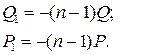
1.7. Однородные уравнения. Функция f (x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:

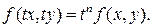
Дифференциальное уравнение вида 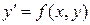называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.

Любое уравнение вида 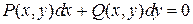является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.

Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.

Рассмотрим однородное уравнение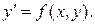

Так как функция f (x, y) – однородная нулевого измерения, то можно записать:

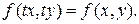
Поскольку параметр t вообще говоря произвольный, предположим, что 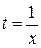. Получаем:

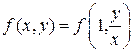
Правая часть полученного равенства зависит фактически только от одного аргумента 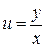, т.е.

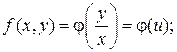
Исходное дифференциальное уравнение таким образом можно записать в виде:

Далее заменяем y = ux, .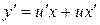

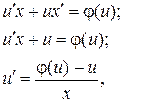
таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.

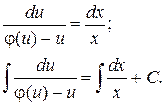
Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.

1.8. Уравнения, приводящиеся к однородным. Кроме уравнений, описанных выше, существует класс уравнений, которые с помощью определенных подстановок могут приведены к однородным. Это уравнения вида

.

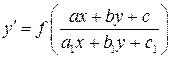Если определитель 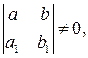то переменные могут быть разделены подстановкой

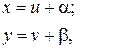
где a и b - решения системы уравнений

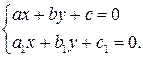
1.9. Уравнения в полных дифференциалах.

Дифференциальное уравнение первого порядка вида:

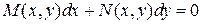
называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции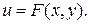

Интегрирование такого уравнения сводится к нахождению функции u, после чего решение легко находится в виде: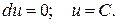

Таким образом, для решения надо определить:

1) в каком случае левая часть уравнения представляет собой полный дифференциал функции u;

2) как найти эту функцию.

Если дифференциальная форма 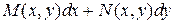является полным дифференциалом некоторой функции u, то можно записать:

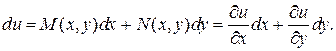
То есть

.

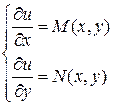Найдем смешанные производные второго порядка, продифференцировав первое уравнение по у, а второе – по х:

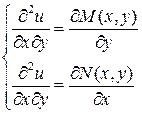
Приравнивая левые части уравнений, получаем необходимое и достаточное условие того, что левая часть дифференциального уравнения является полным дифференциалом.

.

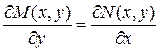Теперь рассмотрим вопрос о нахождении собственно функции u. Проинтегрируем равенство :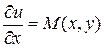

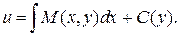
Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию С (у), т.к. при интегрировании переменная у полагается постоянным параметром.

Определим функцию С (у). Продифференцируем полученное равенство по у.

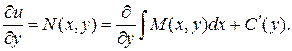
Откуда получаем:

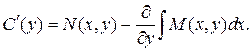
Для нахождения функции С (у) необходимо проинтегрировать приведенное выше равенство. Однако, перед интегрированием надо доказать, что функция С (у) не зависит от х. Это условие будет выполнено, если производная этой функции по х равна нулю.

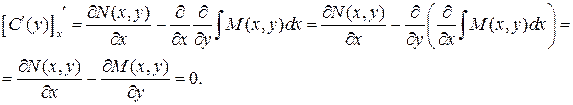
Теперь определяем функцию С (у):

.

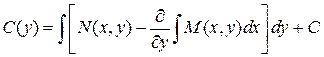Подставляя этот результат в выражение для функции u, получаем:

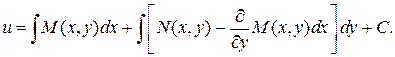
Тогда общий интеграл исходного дифференциального уравнения будет иметь вид:

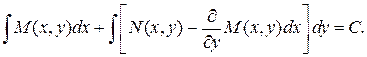
Следует отметить, что при решении уравнений в полных дифференциалах не обязательно использовать полученную формулу. Решение может получиться более компактным, если просто следовать методу, которым формула была получена.

Date: 2015-09-24; view: 407; Нарушение авторских прав