
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Марковские процессы (м.п.)
|
|
М.п. обладают отсутствием последствия. Т.е. если рассматривать текущее состояние процесса 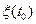 - как настоящее, совокупность возможных состояний
- как настоящее, совокупность возможных состояний 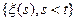 - как прошлое, совокупность возможных состояний
- как прошлое, совокупность возможных состояний 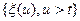 - как будущее, то для м.п. при фиксированном настоящем будущее не зависит от прошлого, а определяется лишь настоящим. Т. е. вероятностное распределение состояния процесса в момент времени
- как будущее, то для м.п. при фиксированном настоящем будущее не зависит от прошлого, а определяется лишь настоящим. Т. е. вероятностное распределение состояния процесса в момент времени 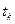 зависит лишь от того, в каком состоянии процесс находился в ближайшем прошлом (при
зависит лишь от того, в каком состоянии процесс находился в ближайшем прошлом (при 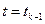 ) но не зависит от его состояний, предшествующих
) но не зависит от его состояний, предшествующих 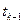 .
.
Марковские случайные процессы названы по имени выдающегося русского математика А.А.Маркова (1856-1922), впервые начавшего изучение вероятностной связи случайных величин и создавшего теорию, которую можно назвать "динамикой вероятностей". В дальнейшем основы этой теории явились исходной базой общей теории случайных процессов, а также таких важных прикладных наук, как теория диффузионных процессов, теория надежности, теория массового обслуживания и т.д. На практике марковские процессы в чистом виде обычно не встречаются. Но имеются процессы, для которых влиянием «предыстории» можно пренебречь и при изучении таких процессов можно применять марковские модели. В настоящее время теория марковских процессов и ее приложения широко применяются в самых различных областях.
Марковские процессы являются моделями очень многих процессов в естественных науках
· Биология: процессы рождения и гибели - популяции, мутации, эпидемии.
· Физика: радиоактивные распады, теория счетчиков элементарных частиц, процессы диффузии.
· Химия: теория следов в ядерных фотоэмульсиях, вероятностные модели химической кинетики.
· Астрономия: теория флуктуационной яркости млечного пути.
· Теория массового обслуживания: телефонные станции, ремонтные мастерские, билетные кассы, справочные бюро, станочные и другие технологические системы, системы управления гибких производственных систем, обработка информации серверами.
ЕОнегин
Пусть в настоящий момент t0 система находится в определенном состоянии S 0. Мы знаем характеристики состояния системы в настоящем и все, что было при t < t 0 (предысторию процесса). Можем ли мы предсказать будущее, т.е. что будет при t > t 0? В точности – нет, но какие-то вероятностные характеристики процесса в будущем найти можно. Например, вероятность того, что через некоторое время 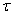 система S окажется в состоянии S 1 или останется в состоянии S 0 и т.д.
система S окажется в состоянии S 1 или останется в состоянии S 0 и т.д.
Пример. Система S – группа самолетов, участвующих в воздушном бою. Пусть x – количество «красных» самолетов, y – количество «синих» самолетов. К моменту времени t 0 количество сохранившихся (не сбитых) самолетов соответственно – x 0, y 0. Нас интересует вероятность того, что в момент времени 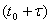 численный перевес будет на стороне «красных». Эта вероятность зависит от того, в каком состоянии находилась система в момент времени t 0, а не от того, когда и в какой последовательности погибали сбитые до момента t 0 самолеты.
численный перевес будет на стороне «красных». Эта вероятность зависит от того, в каком состоянии находилась система в момент времени t 0, а не от того, когда и в какой последовательности погибали сбитые до момента t 0 самолеты.
Дискретные цепи Маркова –
м.п. со счетными состояниями и моментами времени. Переходы из состояния в состояние возможны только в целочисленные моменты времени
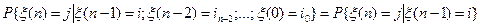
Число 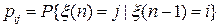 называется вероятностью перехода системы из состояния
называется вероятностью перехода системы из состояния 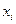 в состояние
в состояние  за один шаг в момент времени
за один шаг в момент времени  . Если переходная вероятность не зависит от
. Если переходная вероятность не зависит от  , то цепь Маркова называется однородной.
, то цепь Маркова называется однородной.
Ниже мы будем рассматривать однородные цепи.
 Матрица P, элементами которой являются вероятности перехода
Матрица P, элементами которой являются вероятности перехода  , называется переходной матрицей:
, называется переходной матрицей: 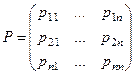 Она является стохастической:
Она является стохастической:  ;
; 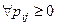 .
. 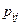 -условные вероятности.
-условные вероятности.
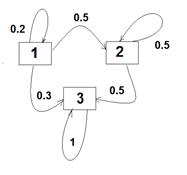
Садовник в результате химического анализа почвы оценивает ее состояние одним из трех чисел — хорошее (1), удовлетворительное (2) или плохое (3). В результате наблюдений на протяжении многих лет садовник заметил, что продуктивность почвы в текущем году зависит только от ее состояния в предыдущем году. Поэтому вероятности перехода почвы из одного состояния в другое можно представить следующей цепью Маркова с матрицей P1:
| 0.20 | 0.50 | 0.30 |
| 0.00 | 0.50 | 0.50 |
| 0.00 | 0.00 | 1.00 |
. Однако в результате агротехнических мероприятий садовник может изменить
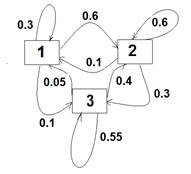
переходные вероятности в матрице P1. Тогда матрица P1 заменится на матрицу P2:
| 0.30 | 0.60 | 0.10 |
| 0.10 | 0.60 | 0.30 |
| 0.05 | 0.40 | 0.55 |
Матрица 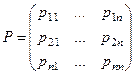
является с.
 Матрица перехода за
Матрица перехода за  шагов
шагов  .
.
Рассмотрим, как изменяются состояния процесса с течением времени. Будем рассматривать процесс в последовательные моменты времени, начиная с момента 0. Зададим начальное распределение вероятностей 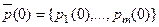 , где m - число состояний процесса,
, где m - число состояний процесса, 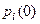 - вероятность нахождения процесса в состоянии i в начальный момент времени.
- вероятность нахождения процесса в состоянии i в начальный момент времени.  Вероятность
Вероятность 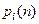 называется безусловной вероятностью состояния i в момент времени
называется безусловной вероятностью состояния i в момент времени  .
. 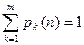 . Компоненты вектора
. Компоненты вектора 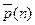 показывают, какие из возможных состояний цепи в момент времени n являются наиболее вероятными.
показывают, какие из возможных состояний цепи в момент времени n являются наиболее вероятными.
Знание последовательности 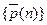 при
при 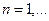 позволяет составить представление о поведении системы во времени.
позволяет составить представление о поведении системы во времени.

Если задано начальное распределение 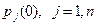 , то
, то 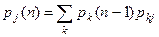
Цепь Маркова полностью определена, если заданы начальное распределение и матрица перехода за 1 шаг
Уравнение Колмогорова-Чепмена (равенство Маркова)
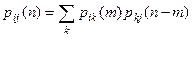
.
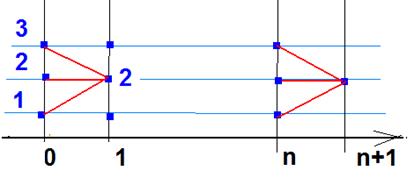
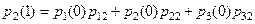
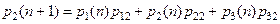
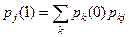
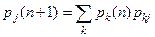
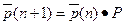
Классификация состояний цепи. По Колмогорову
1. Состояние 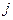 достижимо из состояния
достижимо из состояния 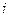 , если существует такое
, если существует такое 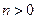 , что
, что 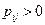 .
.
2. Состояния 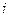 и
и 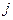 называются сообщающимися, если они достижимы друг из друга
называются сообщающимися, если они достижимы друг из друга
3. Состояние 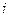 называется несущественным, если существует такое состояние
называется несущественным, если существует такое состояние 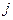 , что
, что 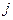 достижимо из состояния
достижимо из состояния 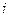 , а
, а 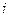 недостижимо из состояния
недостижимо из состояния 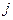 . Состояния
. Состояния 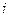 называется существенным в противном случае.
называется существенным в противном случае.
Множество всех существенных состояний разбивается на непересекающиеся классы сообщающихся состояний так, что любые два состояния из одного класса сообщаются между собой, а для любых двух состояний 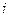 и
и 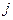 из разных классов
из разных классов 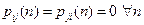 . Цепь Маркова, все состояния которой составляют один класс сообщающихся состояний, называется неразложимой.
. Цепь Маркова, все состояния которой составляют один класс сообщающихся состояний, называется неразложимой.
Пусть 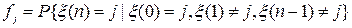
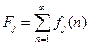
 -вероятность того, что система впервые вернется в
-вероятность того, что система впервые вернется в 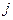 за
за 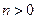 шагов
шагов 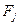 вероятность того, что система когда-нибудь вернется
вероятность того, что система когда-нибудь вернется
4.Состояние 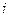 называется возвратным, если вероятность
называется возвратным, если вероятность 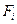 =1, и невозвратным при
=1, и невозвратным при 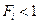 .
.
5.Состояние 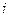 называется нулевым, если
называется нулевым, если 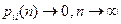 и ненулевым в противном случае.
и ненулевым в противном случае.
6.Состояние 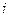 называется периодическим, если наибольший общий делитель
называется периодическим, если наибольший общий делитель 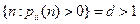
Основные теоремы
Т1. Для того, чтобы состояние 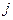 было возвратным, необходимо и достаточно, чтобы
было возвратным, необходимо и достаточно, чтобы 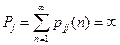 , если
, если 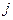 невозвратно, то
невозвратно, то  .
.
Теорема солидарности.
Если цепь Маркова неразложима, то все ее состояния принадлежат к одному и тому же типу: если хотя бы одно из них возвратное, то все возвратные; если хотя бы одно из них нулевое, то все нулевые; если хотя бы одно периодичное с периодом 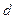 , то все периодичные с периодом
, то все периодичные с периодом 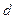 .
.
Неразложимая цепь Маркова называется периодической, если все состояния периодичны с периодом 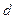 .
.
Для однородных конечных цепей Маркова элементы  матрицы
матрицы  определяются по формуле Перрона:
определяются по формуле Перрона:
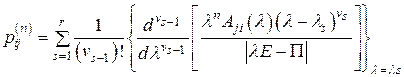 ,
,
где 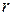 – число различных характеристических чисел (корней уравнения
– число различных характеристических чисел (корней уравнения 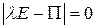 , где
, где 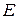 – единичная матрица),
– единичная матрица), 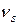 – их кратность
– их кратность 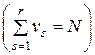 , а
, а 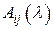 – алгебраическое дополнение для элемента
– алгебраическое дополнение для элемента 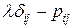 в определителе
в определителе
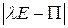 ,
, 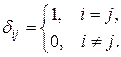
Эргодические цепи Маркова.
Будем рассматривать только однородные цепи Маркова с конечным или счетным числом состояний. Для таких цепей при определенных условиях выполняется следующее свойство:
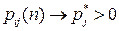 при
при 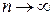 , причем предельное распределение
, причем предельное распределение 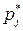 вероятностей состояний ЦМ не зависит от начального распределения, а определяется лишь переходной матрицей Р. В этом случае говорят, что ЦМ обладает эргодическим свойством, которое фактически означает, что вероятности состояний по мере увеличения п практически перестают изменяться, а система, описываемая соответствующей цепью, переходит в стационарный режим функционирования.
вероятностей состояний ЦМ не зависит от начального распределения, а определяется лишь переходной матрицей Р. В этом случае говорят, что ЦМ обладает эргодическим свойством, которое фактически означает, что вероятности состояний по мере увеличения п практически перестают изменяться, а система, описываемая соответствующей цепью, переходит в стационарный режим функционирования.
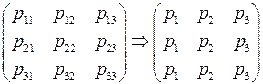
Однородная цепь Маркова, для которой вероятности 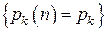 не зависят от
не зависят от 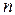 , называется стационарной. Распределение вероятностей
, называется стационарной. Распределение вероятностей 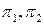 называется стационарным, если
называется стационарным, если 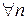
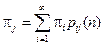
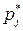 всегда стационарно, а
всегда стационарно, а 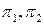 не всегда предельны
не всегда предельны
Пр 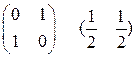
В общем случае вероятности 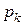 , если они существуют, находятся в результате предельного перехода
, если они существуют, находятся в результате предельного перехода
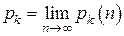 ,
, 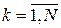 ,
,
и называются финальными вероятностями. Если начальные вероятности 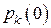 совпадают с соответствующими финальными вероятностями
совпадают с соответствующими финальными вероятностями 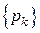 , то цепь Маркова будет стационарной
, то цепь Маркова будет стационарной
Теорема (эргодическая). Пусть однородная ЦМ имеет переходную матрицу Р и обладает следующими свойствами:
1) цепь неразложима и непериодична;
2) найдется такое состояние 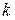 , что время возвращения в него, т. е. дискретная случайная величина
, что время возвращения в него, т. е. дискретная случайная величина 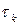 с распределением
с распределением 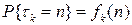 имеет конечное математическое ожидание
имеет конечное математическое ожидание
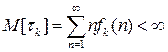
Выполнение условий 1, 2 необходимо и достаточно для того, чтобы для любых i,j = 0,1,... существовали не зависящие от 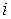 пределы
пределы 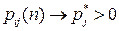 при
при 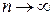 .
.
Числа 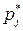 являются единственным решением системы уравнений
являются единственным решением системы уравнений
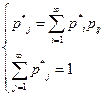 (**)
(**)
(**) следует из. Для стационарного режима 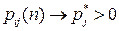 при
при 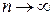 вероятность
вероятность 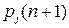 совпадает с
совпадает с  :
: 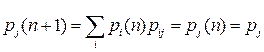
Нахождение 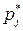
1) составить систему уравнений 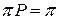
2) заменить в полученной системе одно из уравнений на условие нормировки
3) решить систему
Date: 2015-09-24; view: 868; Нарушение авторских прав