
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Потік магнітного поля. Теорема Гауса для магнітного поля в вакуумі
|
|
Нехай в просторі задана деяка поверхня S будь-якої форми. Виділимо елементарну площадку dS.

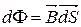
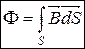 (7.1)
(7.1)
[Ф]=1 Вб =1 Тл×м2= 1 Н×м2/А×м= 1 В×с
1 Вб – це потік магнітного поля при індукції 1 Тл крізь площадку в 1 м2, розташовану ^ до вектора  .
.

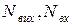 - кількість магнітних ліній, що виходять і входять в замкнену поверхню.
- кількість магнітних ліній, що виходять і входять в замкнену поверхню.
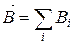
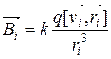 - поле заряда q, який рухається рівномірно і повільно.
- поле заряда q, який рухається рівномірно і повільно.


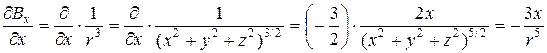


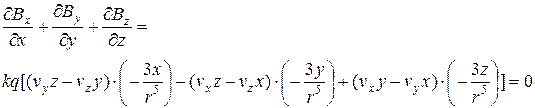
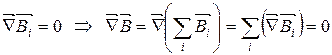
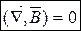 (7.2)
(7.2)
Вираз (7.2) є теорема Гауса в локальній (або диференціальній) формі:
дивергенція магнітного поля всюди дорівнює нулю.
Дивергенція - це питома алгебраїчна потужність джерел. Отже, в природі не існує магнітних зарядів, які були б джерелами магнітного поля.
За теоремою Остроградського-Гауса:
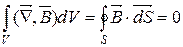 , S -це замкнена поверхня, яка оточує об¢єм V. Отже,
, S -це замкнена поверхня, яка оточує об¢єм V. Отже,  (7.3)
(7.3)
Це теорема Гауса для магнітного поля в вакуумі в інтегральній формі:
потік вектора магнітної індукції крізь довільну замкнену поверхню дорівнює нулю.
Отже, лінії магнітного поля завжди замкнені.
§2 Теорема про циркуляцію магнітного поля у вакуумі.
 Циркуляція вектора
Циркуляція вектора  :
:

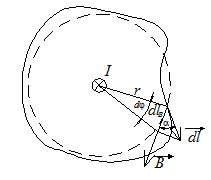
Розглянемо прямий струм у тонкому провіднику, обмежимо його плоским контуром довільної форми.
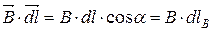


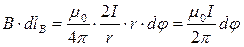

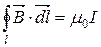
Отже, циркуляція вектора  за контуром l дорівнює добутку магнітної сталої на силу струму, що охоплюється цим контуром.
за контуром l дорівнює добутку магнітної сталої на силу струму, що охоплюється цим контуром.
Якщо струм не охоплюється контуром:
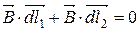
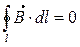


 , якщо струм
, якщо струм
охоплюється
 контуром
контуром
0, якщо струм
не охоплюється
контуром
інтегрування
Знак циркуляції може бути “+” і “-”. Знак циркуляції можна врахувати, вважаючи I алгебраїчною величиною. Додатнім вважають струм, напрямок якого пов¢язують з напрямом правила правого свердлика.
 Нехай маємо струми I1, I2,…, IN .
Нехай маємо струми I1, I2,…, IN .


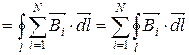
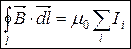 (7.4)
(7.4)
Циркуляція магнітного поля (вектора  ) постійних струмів в вакуумі за довільним контуром l дорівнює добутку магнітної сталої на алгебраїчну суму струмів, що охоплюються цим контуром.
) постійних струмів в вакуумі за довільним контуром l дорівнює добутку магнітної сталої на алгебраїчну суму струмів, що охоплюються цим контуром.
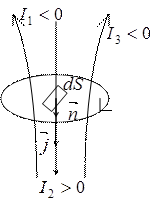
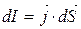
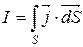
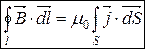 (7.5)
(7.5)
Той факт, що циркуляція вектора  в загальному випадку не дорівнює нулю, говорить про те, що магнітне поле не є потенціальним на відміну від електростатичного.
в загальному випадку не дорівнює нулю, говорить про те, що магнітне поле не є потенціальним на відміну від електростатичного.
Поняття скалярного потенціалу відсутнє.
§3 Обчислення магнітних полів за допомогою теореми про циркуляцію.
1) Магнітне поле прямолінійного провідника радіуса R нескінченної довжини з струмом I.
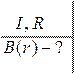
1. 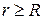

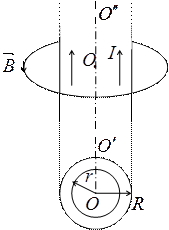
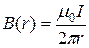

2. 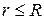
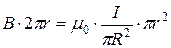
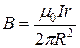


2) Магнітне поле нескінченно довгого соленоїда
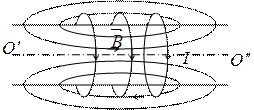 n – кількість витків на одиницю довжини
n – кількість витків на одиницю довжини
Можна показати, що магнітне поле нескінченно довгого соленоїда зосереджене всередині каркаса, а назовні відсутнє взагалі.
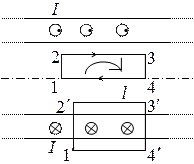

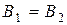
У будь-якій точці соленоїда поле однорідне, і в будь-якій точці магнітна індукція дорівнює значенню магнітної індукції на осі.
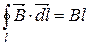
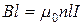
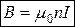 (7.6)
(7.6)
n×I – кількість ампер-витків.
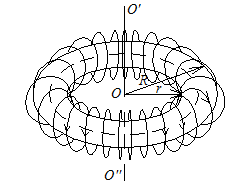
3) Магнітне поле тороїда
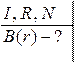
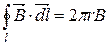
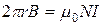
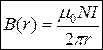 (7.7)
(7.7)
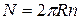


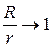

Алгоритм розв¢язку задач:
Аналіз симетрії магнітного поля.
Раціональний вибір контура.
Безпосереднє обчислення циркуляції вздовж контура.
Застосування теореми і вираження  .
.
§4 Локальна форма теореми про циркуляцію.

За теоремою Стокса: 
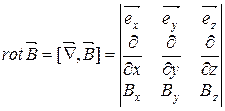
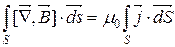
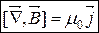 (7.8)
(7.8)
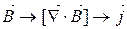
У кожній точці простору в вакуумі ротор магнітного поля дорівнює добутку магнітної сталої на вектор густини струму в цій точці.
§5 Потенціальні та вихрові поля
| Електростатичне поле | Магнітне поле | |
| Силова характеристика | 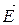
| 
|
| Теорема Гауса в інтегральній формі | 
| 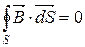 поле соленоїдне поле соленоїдне
|
| Теорема Гауса в локальній формі | 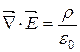
|  поле бездівергентне
поле бездівергентне
|
| Теорема про циркуляцію | 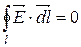 поле потенціальне поле потенціальне
| 
|
| Теорема про циркуляцію в локальній формі | 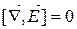
|  вихрове поле вихрове поле
|
Розділ 8. Магнітне поле в речовині. Магнетики.
§ 1. Магнітний момент атомів та молекул. Намагнічування. Вектор 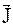 .
.
Атом – мікроскопічний контур з магнітним моментом

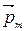
І

За відсутності зовнішніх полів речовина не проявляє магнітних властивостей, внаслідок теплового руху атомів. При дії магнітного поля 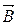 виникає сумарний магнітний момент.
виникає сумарний магнітний момент.
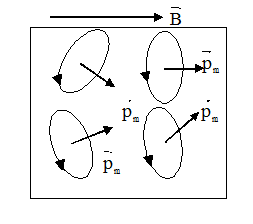
Під дією зовнішнього магнітного поля магнітні моменти набувають переважної орієнтації в напрямку поля, внаслідок чого речовина намагнічується.
Намагнічуванням називається явище виникнення в речовині об’ємного макроскопічного магнітного моменту.
Вектор намагнічування (намагніченість) – сумарний магнітний момент всіх молекул, визначений за фізично нескінченно малим об’ємом взятим в околі точки, що розглядається.
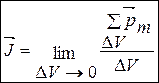 (8.1)
(8.1)

Залежить від:
а) величини магнітного поля в точці;
б) конкретних фізичних властивостей речовини
§2 Струми намагнічування. Теорема Гауса для магнітного поля в речовині.
Намагнічування речовини обумовлене переважною орієнтацією векторів 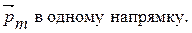
Те ж саме можна сказати і про елементарні кільцеві струми, пов’язані з кожною молекулою. Їх називають молекулярними струмами.

При намагнічуванні відбувається таке впорядкування руху зарядів в молекулах, в результаті якого по поверхні будь-якого виділеного в намагніченій речовини об’єму циркулює макроскопічний струм, що називається струмом намагнічення.
Струми, що утворюють магнітні моменти і не дають вклад в макроскопічні струми провідності, називаються струмами намагнічування.
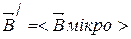
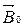 - зовнішнє поле в речовині
- зовнішнє поле в речовині
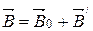
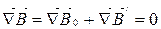
 (8.2)
(8.2)
Теорема Гауса в речовині має такий самий вигляд, як і у вакуумі.
 (8.3)
(8.3)
Магнітне поле соленоїдальне.
§ 3. Теорема про циркуляцію магнітного поля в речовині. Вектор напруженості магнітного поля Н.
У вакуумі:
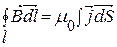
Застосовуючи формулу Стокса: 
В речовині:
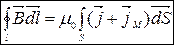 (8.4)
(8.4)
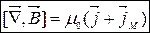 (8.5)
(8.5)
Треба знайти такий допоміжний вектор, ротор якого визначався б лише густиною макроскопічних струмів провідності.
 Виберемо всередині речовини довільну поверхню S, яка обмежена контуром l і обчислимо
Виберемо всередині речовини довільну поверхню S, яка обмежена контуром l і обчислимо  .
.
В цю суму ненульовий вклад дають струми, які “нанизані”, бо всі інші або не перетинають поверхню, або перетинають її двічі.

Нанизані на цей контур будуть лише молекулярні струми, центри яких знаходяться всередині циліндра.
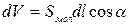
Сумарний струм, що охоплюється елементом dl:
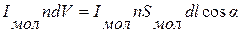

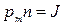
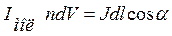
-скалярний добуток двох векторів
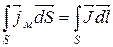
(8.6)

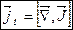 (8.7)
(8.7)
Якщо в рівнянні (8.5) замінити 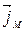 , то:
, то:
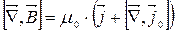
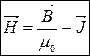 (8.8)
(8.8)
У вакуумі: 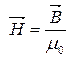
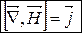 (8.9)
(8.9)
- локальна форма теореми про циркуляцію вектора 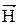 .
.
Ротор вектора напруженості магнітного поля в будь-якій точці магнетика дорівнює густині струмів в цій самій точці.
Проінтегруємо формулу (8.6) за будь-якою поверхнею S:
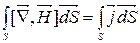
 (8.10)
(8.10)
(8.10) – теорема про циркуляцію магнітного поля в речовині.
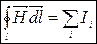 (8.10)
(8.10)
Циркуляція вектора напруженості магнітного поля за довільним контуром дорівнює алгебраїчній сумі макроскопічних струмів провідності, що охоплені цим контуром.
§4 Магнітна сприйнятливість. Магнітна проникність речовини.

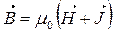
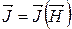
В ізотропних речовинах та не дуже сильних магнітних полях залежність має вигляд:
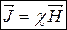 (8.11)
(8.11)
χ – міра відгуку речовини на намагнічування, магнітна сприйнятливість речовини.
χ =1 χ >0 χ<0
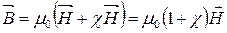
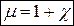 (8.12)
(8.12)
μ – відносна магнітна проникність речовини
Для ізотропних магнетиків:
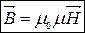 (8.13)
(8.13)
Таким чином вектор 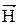 спрямований як і вектор
спрямований як і вектор 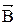 , але в μ0μ раз менший за модулем.
, але в μ0μ раз менший за модулем.
У вакуумі:

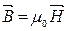
§5 Умови на межі поділу двох магнетиків.
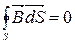

1 Умови для нормальних складових 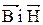 .
.


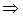
 (8.14)
(8.14)

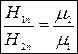 (8.15)
(8.15)
2 Умови для тангенціальних складових 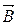 i
i 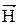 .
.
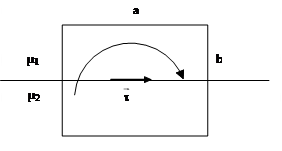

Якщо на межі поділу немає макроскопічних струмів провідності, то циркуляція дорівнює нулю.
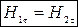 (8.16)
(8.16)
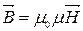
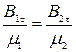
 (8.17)
(8.17)
Отже, при переході крізь межу поділу двох магнетиків нормальна складова 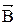 і тангенціальна складова
і тангенціальна складова 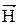 неперервні, а складові Bτ і
неперервні, а складові Bτ і 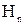 зазнають розриву.
зазнають розриву.
На межі поділу двох середовищ 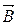 поводить себе так само, як
поводить себе так само, як  , а
, а  як
як 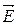 .
.
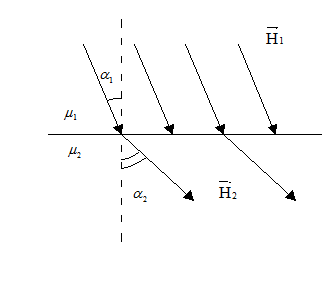
3. Заломлення ліній вектора 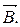


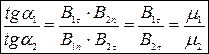
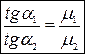 (8.18)
(8.18)
При переході в магнетик з більшим значенням  лінії магнітної індукції відхиляються від нормалі до поверхні, це викликає їх згущення і
лінії магнітної індукції відхиляються від нормалі до поверхні, це викликає їх згущення і  .
.
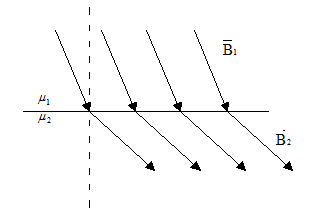
4. Магнітне екранування.
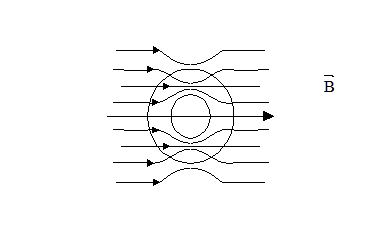
Магнітне екранування ніколи не буває повним (на відміну від електричного). Лінії не можуть обриватися на поверхні, лише змінюють напрямок.
5. Розрив ліній 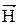

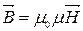

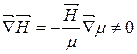
 <
< 
На межі поділу спостерігається розрив ліній 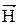 внаслідок існування струмів намагнічування.
внаслідок існування струмів намагнічування.
§6 Магнетики.
1. Типи магнетиків.
В магнітному відношенні всі речовини поділяються на два класи: слабомагнітні (пара- та діамагнетики) та сильномагнітні (феромагнетики).
Визначним фактором приналежності магнетика до того чи іншого класу є значення 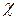 .
.
Діамагнетики:

 ~
~ 
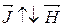
інертні гази, деякі метали: Cu, Be, Zn, Ag, Au;
неорганічні сполуки:  ;
;
Парамагнетики:
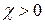
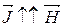
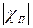 ~
~ 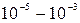
гази: 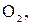 NO;
NO;
елементи: Li, Na, Ca;
неорганічні сполуки: CaO;
Феромагнетики:

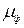 ~
~ 
Елементи в твердому кристалічному стані:
Fe 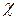 ~
~ 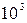
Ni 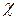 ~
~ 
Сплави, рідкоземельні елементи.
Доменна структура феромагнетиків.
В твердих речовинах між електронами існує особлива обмінна взаємодія, що не має аналогів в класичній фізиці. В деяких твердих речовинах у відповідності з особливістю їх кристалічної структури і будовою атому обмінна взаємодія дуже велика. Ця взаємодія приводить до того, що спінові магнітні моменти електронів великої кількості атомів встановлюються строго паралельно один до одного. В результаті утворюються невеликі макроскопічні ділянки спонтанного намагнічування, що називаються доменами.
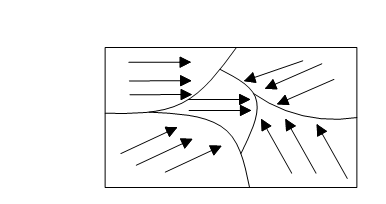
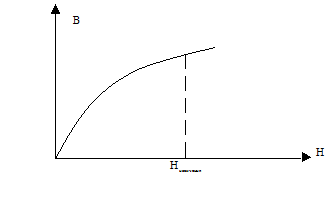
Крива Столетова:

Особливості:
1) нелінійність намагнічування
2) наявність насичення
Магнітний гістерезис
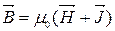
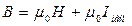
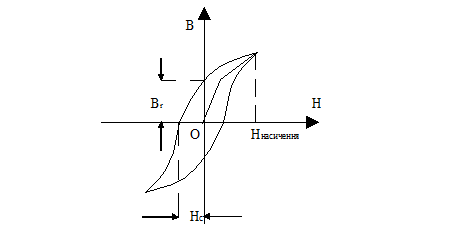
За величиною площі петлі гістерезиса магнетики поділяються на магнітом’які та магнітожорсткі.
Магнітом’які: використовуються для осердя в трансформаторах та індукційних кружцях.
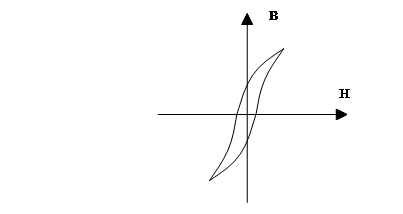

Магнітожорсткі:
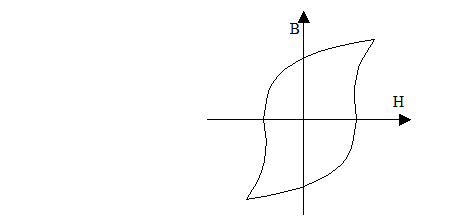
Ці феромагнетики застосовуються в якості постійних магнітів та як елементи логічних комірок в обчислювальній техніці та автоматиці.
2 Особливості визначення магнітної проникності і температурна залежність μ.
Магнітна проникність μ – макроскопічний параметр, який характеризує магнітні властивості різних магнетиків і для кожного однорідного магнетика є матеріальною константою. Магнітну проникність μ визначають експериментально.
Для кожного феромагнетика є певна температура Тс за якої речовина втрачає феромагнітні властивості. Ця температура називається точкою Кюрі. При температурі, вищій за точку Кюрі, феромагнетик стає звичайним парамагнетиком, магнітна сприйнятливість якого підкорюється закону Кюрі-Вейса.
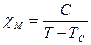
С - стала Кюрі
Т - абсолютна температура
При охолодженні феромагнетика нижче за точку Кюрі у ньому знову виникають домени.
Розділ 9. Електромагнітна індукція.
§1 Спостереження та експериментальні закономірності явища.
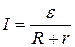 ,
,
але при переміщенні контура в магнітному полі 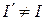 .
.
В 1831 Фарадей відкрив явище електромагнітної індукції.
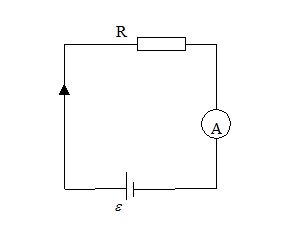
Схема досліду:
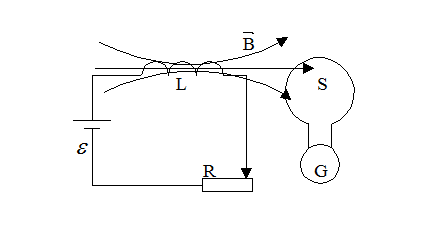
Явищем електромагнітної індукції називається виникнення ЕРС (і струму) в замкненому провідному контурі при зміні магнітного потоку крізь площу, обмежену контуром.
Властивості явища:
Величина ЕРС індукції і індукційного струму не залежить від конкретних причин зміни потоку.
При переміні характеру зміни потоку напрямок індукційного струму стає протилежним.
Величина індукційного струму залежить не від зміни магнітного потоку 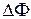 , а від швидкості його зміни.
, а від швидкості його зміни.
§2 Основний закон електромагнітної індукції.
Закон встановлений Фарадеєм в результаті узагальнення дослідних фактів. В 1845 р. його математичне визначення дав фон Нейман.
 (9.1)
(9.1)
ЕРС індукції, що виникає в контурі, дорівнює швидкості зміни потоку індукції зовнішнього магнітного поля крізь поверхню, обмежену контуром, із знаком “мінус”.
Для окремого випадку можна одержати цю формулу із закону збереження енергії, як це зроблено Гельмгольцем.
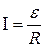
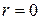

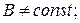 І=І΄
І=І΄
За час dt джерело виконує роботу 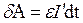 ;
;

Частина енергії піде на рух контура в магнітному полі, а частина – на виділення теплоти.

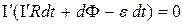
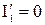

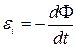
Таким чином в контурі, що рухається в магнітному полі, струм визначається не лише ЕРС гальванічного елемента, а й доданком 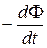 . В електричному контурі діє додаткова ЕРС, викликана зміною магнітного потоку через площу контуру – це і є ЕРС індукції.
. В електричному контурі діє додаткова ЕРС, викликана зміною магнітного потоку через площу контуру – це і є ЕРС індукції.
Якщо 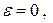 то
то
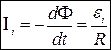 (9.2)
(9.2)
§3 Напрямок індукційного струму. Правило Ленца.
В 1833 р. Ленц встановив експериментальне правило: індукційний струм завжди спрямований таким чином, що утворене ним магнітне поле протидіє зміні магнітного потоку, який викликає цей струм.

Принцип Лє Шател’є і Брауна:
Якщо система знаходиться в стані стійкої рівноваги, то будь-який процес, викликаний в ній зовнішнім впливом, завжди спрямований таким чином, що намагається знищити зміни, спричинені зовнішнім впливом.
§4 Явище самоіндукції. Індуктивність контуру.
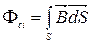 І=І(t)
І=І(t)
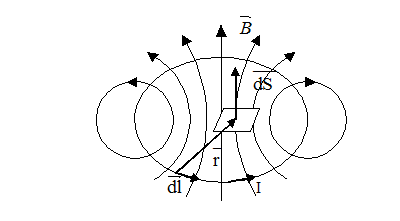
Зміна струму в контурі призводить до виникнення ЕРС індукції в тому ж самому контурі. Це явище називається ЕРС самоіндукції.
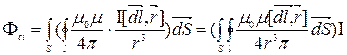
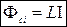 (9.3)
(9.3)
Коефіцієнт пропорційності між І та Ф називається індуктивністю контура.
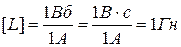
1Гн – це індуктивність такого контуру, який при протіканні ним струму в 1А виявляється зчепленим з магнітним контуром 1Вб.
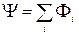
 (9.4)
(9.4)
– повний магнітний потік, або потокозчеплення
Індуктивність контуру визначається властивостями контуру (котушки): площею, радіусом витка і т.д.
Приклад: Обчислення індуктивності нескінченно довгого соленоїда із струмом.

 (9.5)
(9.5)
Обчислимо ЕРС самоіндукції:
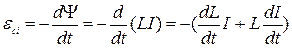
Якщо контур жорсткий та знаходиться в магнітному середовищі, де  , то
, то  .
.
 (9.6)
(9.6)
§5 Струм при замиканні та розмиканні електричного кола з індуктивністю.
1 Розмикання кола.
Схема:
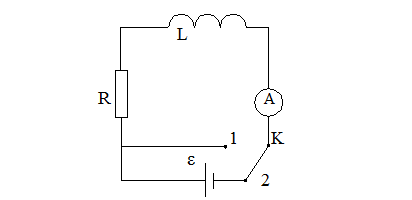
К1:  ,
,
t=0, К1→2, 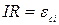 ,
,  ,
,
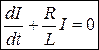 . (9.7)
. (9.7)
 ,
, 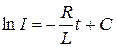 ,
,
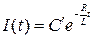 ,
,
t=0, 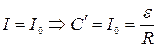 ,
,
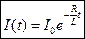 .(9.8)
.(9.8)
 - стала часу кола
- стала часу кола
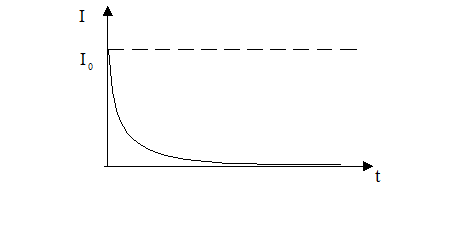
Висновок: при розмиканні електричний струм не обертається миттєво на нуль, а спадає за експоненціальним законом.
2 Замикання кола.
К2: І=0,
t=0, К2→1, 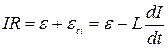 ,
,
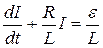 , (9.9)
, (9.9)
 .
.
Якщо t=0, I=0 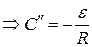 ,
,
 (9.10)
(9.10)
τ – час релаксації (час, за який сила струму зміниться в е раз);
Після замикання електричного кола з індуктивністю сила струму зростає поступово.
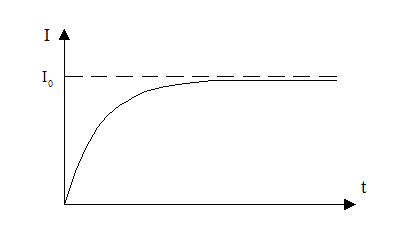
 при t→ ∞
при t→ ∞
§6 Взаємна індукція.
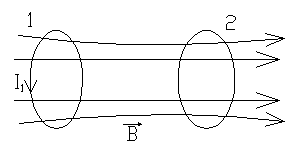
Струм I1 утворює крізь контур 2 магнітний потік
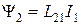
Якщо 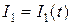 , то
, то
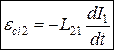 (9.11)
(9.11)
– якщо контур жорсткий, а  (відсутній феромагнетик).
(відсутній феромагнетик).
Якщо 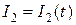 , то
, то
 (9.12)
(9.12)
Такі 2 контури називають зв’язаними.
Явище виникнення ЕРС в одному з контурів при зміні сили струму в іншому називають взаємною індукцією. Коефіцієнти пропорційності L12 і L21 називають взаємною індуктивністю контурів або коефіцієнтами взаємної індукції.
За відсутності феромагнетика:
Теорема взаємності: 
§7 Енергія магнітного поля.
У процесі зміни сили струму в контурі джерело сторонніх ЕРС виконує роботу проти ε і.
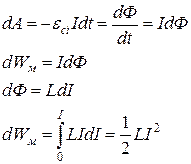
 (9.13)
(9.13)
– енергія магнітного поля замкненого провідного контуру зі струмом I i L.
Енергія магнітного поля розподілена в усьому просторі, де локалізоване поле.
Соленоїд зі струмом у вакуумі:
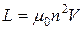

 (9.14)
(9.14)
- об’ємна густина енергії магнітного поля в околі кожної точки простору визначається значенням векторів поля в цій точці.
§8 Природа електромагнітної індукції.
1. Виникнення ЕРС самоіндукції в провіднику, що рухається.
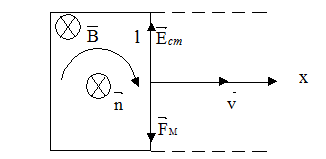
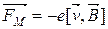 - магнітна складова сили Лоренца
- магнітна складова сили Лоренца
В цьому полі напруженість 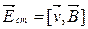 .
.
Дане поле – непотенціальне, тобто поле сторонніх сил.
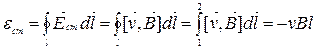

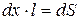
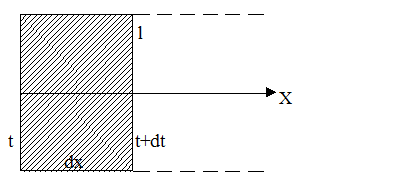
Під час руху замкненого провідника в зовнішньому магнітному полі, в його контурі виникає ЕРС індукції, що дорівнює швидкості зміни потоку індукції крізь поверхню, обмежену контуром.
Якщо в контурі рухається декілька ділянок, то ЕРС дорівнює алгебраїчній сумі швидкостей.
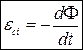 (9.15)
(9.15)
2. Вихрове електричне поле.
Контур знаходиться в електричному полі, що змінюється з часом.
 . З досліду
. З досліду 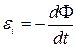 . Нехай
. Нехай 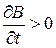
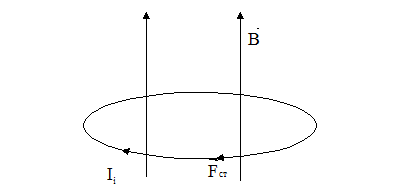
Ці сторонні сили не пов’язані ні з хімічними, ні з тепловими процесами в дроті, вони не можуть мати магнітну природу. Єдина можливість: 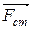 повинні мати електричну природу – це означає, що в кожній точці провідника існує електричне поле.
повинні мати електричну природу – це означає, що в кожній точці провідника існує електричне поле.
Гіпотеза Максвела:
Будь-яке змінне в часі магнітне поле збуджує в оточуючому просторі електричне поле.
Згідно з визначенням ЕРС маємо:
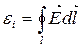
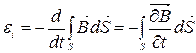
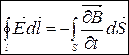 (9.16)
(9.16)

 (9.17)
(9.17)
(9.16) і (9.17) рівняння являють собою закон електромагнітної індукції в трактовці Максвела.
(9.17): Швидкість зміни магнітного поля 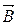 визначає ротор напруженості поля в цій самій точці.
визначає ротор напруженості поля в цій самій точці.
У відповідності з тим, що  і
і  , електричне поле не потенціальне.
, електричне поле не потенціальне.
Електричне поле, що збуджується змінним магнітним полем – вихрове.
Якщо 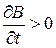 , то
, то 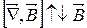
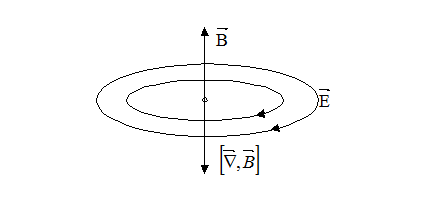
Лінії замкнені тому, що 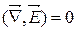 .
.
Формулювання Максвела більш загальне, ніж формулювання Фарадея. Максвел бачить сутність електромагнітної індукції в збудженні електричного поля.
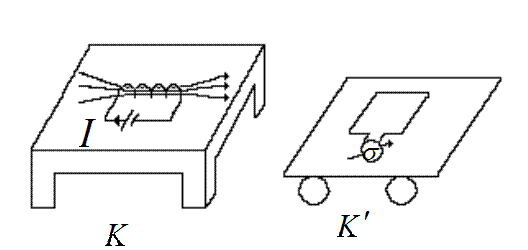 |
3. Відносність механізмів електромагнітної індукції
У загальному випадку, коли провідник рухається в змінному магнітному полі, індукційний струм виникає внаслідок дії повної сили Лоренца  .
.
Оскільки існує взаємозвязок між електричним і магнітним полем, то розглядати їх окремо некоректно.
Розділ 10. Рівняння Максвела.
§1 Струм зміщення.
 (10.1)
(10.1)
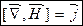 (10.2)
(10.2)
В стаціонарному випадку 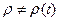 ,
,  ,
, 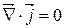
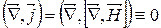 . Отже,рівняння (1) і (2) взаємоузгодженні.
. Отже,рівняння (1) і (2) взаємоузгодженні.
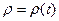 ,
, 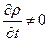 ,
, 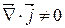 Þ (1) і (2) взаємосуперечливі.
Þ (1) і (2) взаємосуперечливі.
За Максвелом:  ,
, 
 ,
,  ,
, 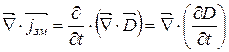
 (10.3)
(10.3)
Струм зміщення являє собою електричне поле, що змінюється в часі. З усіх фізичних властивостей, що має дійсний струм, струм зміщення має лише одну здатність - утворювати магнітне поле.
 (10.4)
(10.4)
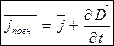 (10.5)
(10.5)
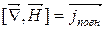
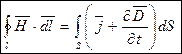 (10.6)
(10.6)
§2 Система рівнянь Максвела.
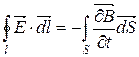
| 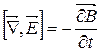
| Закон електромагнітної індукції |

| 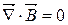
| Теорема Гауса для магнітного поля |
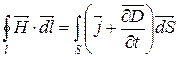
| 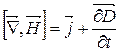
| Показує. що змінне електричне поле утворює у просторі змінне магнітне поле |

| 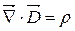
| Теорема Гауса для електричного поля |
Матеріальні співвідношення:
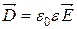
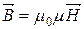
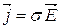 .
.
Диференціальну систему рівнянь доповнюють граничними умовами:
D2n=D1n
E2t=E1t
B2n=B1n
H2t=H1t
| <== предыдущая | | | следующая ==> |
| Основна література | | | Nbsp; зміст |
Date: 2015-09-23; view: 728; Нарушение авторских прав