
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

I: {{128}} ТЗ-1-2-16к
|
|
S: Подлежащее групповых статистических таблиц содержит
-: перечень единиц совокупности
+: группировку единиц совокупности по одному признаку
-: группировку единиц совокупности по нескольким признакам
-: показатели, характеризующие исследуемый объект
V2: {{3}} Тема 3. Статистические показатели.
I: {{129}} ТЗ-1-3-1п.
S: Показатели, характеризующие объемы, размеры социально-экономических явлений, являются
+: абсолютными величинами
-: относительными величинами
-: индексами
-: коэффициентами
I: {{130}} ТЗ-1-3-2п.
S: Показатели, характеризующие объемы, размеры социально-экономических явлений, выражаются … единицами измерения.
-: натуральными
-: трудовыми
-: стоимостными
+: натуральными, трудовыми и стоимостными
I: {{131}} ТЗ-1-3-3п.
S: Показатели, характеризующие количественные соотношения явлений, являются величинами
-: абсолютными
+: относительными
-: натуральными
-: трудовыми
-: стоимостными
I: {{132}} ТЗ-1-3-4п.
S: Показатели, характеризующие количественные соотношения явлений, вычисляются путем
-: деления одноименных величин
-: сложения одноименных величин
-: вычитания одноименных величин
-: деления разноименных величин
+: деления одноименных и/или разноименных величин
I: {{133}} ТЗ-1-3-5п.
S: Отношением разноименных показателей являются относительные величины:
+: интенсивности
-: пространственного сравнения
-: координации
-: плана
I: {{134}} ТЗ-1-3-6п.
S: Путем деления одноименных показателей рассчитываются относительные величины:
-: интенсивности
+: структуры и координации
-: интенсивности и структуры
-: интенсивности и координации
I: {{135}} ТЗ-1-3-7п.
S: Относительной величиной интенсивности является
-: структура ВВП
+: размер ВВП на душу населения
-: доля мужчин в численности населения города
-: процент выполнения плана
I: {{136}} ТЗ-1-3-8п.
S: Количество браков на 1000 жителей, если
| Регион | А | Б |
| Количество браков | ||
| Среднегодовая численность населения |
-: больше в регионе А
+: больше в регионе Б
-: в обоих регионах одинаково
-: вывод сделать невозможно
I: {{137}} ТЗ-1-3-9п.
S: Относительной величиной динамики является
+: процент увеличения инвестиций в нефтедобывающую промышленность за год
-: объем увеличения добычи нефти за год (млн. т.)
-: процент выполнения плана добычи нефти за год
-: объем увеличения инвестиций в нефтедобывающую промышленность за год
I: {{138}} ТЗ-1-3-10п.
S: Быстрее сокращалось производство … в 2002 г. по сравнению с 2001 г.
| Год Товар | ||
| Сахар, т | ||
| Масло, м3 |
-: сахара
+: масла
-: темпы сокращения одинаковы
-: вывод сделать невозможно
I: {{139}} ТЗ-1-3-11п.
S: Относительной величиной динамики является
+: процент увеличения реальной заработной платы за год
-: объем уменьшения дефицита бюджета (млрд. руб.)
-: процент выполнения плана производства
-: объем увеличения выпуска продукции (млн. т)
I: {{140}} ТЗ-1-3-12п.
S: Более высокими были темпы роста
| Год | ||
| Внешний долг | ||
| Выплата долга |
-: суммы долга
-: выплаты долга
+: по обоим показателям темпы одинаковы
-: темпы несравнимы
I: {{141}} ТЗ-1-3-13п.
S: Относительной величиной пространственного сравнения является
-: обеспеченность жильем населения в каждом регионе
-: стоимость 1 м2 жилья в каждом регионе
-: разность стоимости 1 м2 жилья в регионах А и Б
+: отношение стоимости 1 м2 жилья в регионах А и Б
I: {{142}} ТЗ-1-3-14п.
S: Относительной величиной сравнения является отношение
+: минимальной заработной платы к прожиточному минимуму
-: бюджетных расходов на охрану здоровья к годовому бюджету
-: количества мужчин, состоящих в браке к общему количеству мужчин
-: количества лиц с высшим образованием к численности населения
I: {{143}} ТЗ-1-3-15п.
S: Относительной величиной структуры является отношение
+: бюджетных расходов на охрану здоровья к годовому бюджету
-: расходов на охрану здоровья к стоимости коммунальных услуг
-: стоимости коммунальных услуг к покупательной способности рубля
-: прожиточного минимума к минимальной заработной плате
I: {{144}} ТЗ-1-3-16п.
S: Относительной величиной координации является отношение
-: количества занятых в народном хозяйстве региона к количеству лиц с высшим образованием
-: количества мужчин, состоящих в браке к общему количеству мужчин
+: общего количества мужчин к общему количеству женщин
-: количества лиц с высшим образованием к численности населения
I: {{145}} ТЗ-1-3-17п.
S: Относительной величиной пространственного сравнения является отношение:
-: объема перевозки грузов автомобильным транспортом к объему перевозки по железной дороге
-: стоимости перевозки грузов автомобильным транспортом к стоимости перевозки по железной дороге
-: емкости автоматических телефонных станций в городах к емкости в селах
+: численности населения региона А к численности населения в Б
I: {{146}} ТЗ-1-3-18п.
S: Относительной величиной координации является отношение
+: частей целого друг к другу
-: части целого к целому
-: количественной характеристики явления к среде его распространения
-: достигнутого уровня к запланированному
I: {{147}} ТЗ-1-3-19п.
S: Относительной величиной сравнения является отношение
+: аукционной цены акций к их номинальной стоимости
-: стоимости выставленных на аукцион акций к общей стоимости акций
-: стоимости акций в текущем периоде к их стоимости в базисном периоде
I: {{148}} ТЗ-1-3-20п.
S: Относительной величиной структуры является отношение
-: частей целого друг к другу
+: части целого к целому
-: количественной характеристики явления к среде его распространения
-: достигнутого уровня к запланированному
I: {{149}} ТЗ-1-3-21п.
S: Доля сельского населения равна …, если в регионе проживало 5 млн. чел., в том числе в городах 2 млн. чел.
+: 0,6
-: 0,4
-: 2/3
-: 1,5
I: {{150}} ТЗ-1-3-22п.
S: Городских жителей приходится … на 100 сельских, если в регионе проживает 8 млн. чел., в том числе в городах 3 млн. чел.
-: 38
-: 62
+: 60
-: 40
I: {{151}} ТЗ-1-3-23.
Q: Соответствие между видами относительных величин
L1: доля занятых в общей численности экономически активного населения
R1: относительный показатель структуры
L2: потребление продуктов питания в расчете на душу населения
R2: относительный показатель интенсивности
L3: соотношение численности мужчин и женщин в общей численности безработных
R3: относительный показатель координации
L4:
R4: относительный показатель плана
L5:
R5: относительный показатель динамики
L6:
R6: относительный показатель сравнения
I: {{152}} ТЗ-1-3-24.
Q: Соответствие между видами относительных величин:
L1: доля мужчин в общей численности безработных
R1: относительный показатель структуры
L2: потребление молока в расчете на душу населения
R2: относительный показатель интенсивности
L3: соотношение численности мужчин и женщин в общей численности населения
R3: относительный показатель координации
L4:
R4: относительный показатель реализации плана
L5:
R5: относительный показатель динамики
L6:
R6: относительный показатель плана
I: {{153}} ТЗ-1-3-25.
S: Взаимосвязь относительных показателей динамики (ОПД), плана (ОПП) и реализации плана (ОПРП) выражается соотношением:
+: ОПД=ОПП´ОПРП
-: ОПД=ОПП:ОПРП
-: ОПД=ОПП+ОПРП
-: ОПД=ОПП-ОПРП
I: {{154}} ТЗ-1-3-26к.
S: Относительный показатель плана по выпуску продукции
= ### %, если план выполнен на 120%, а прирост выпуска продукции по сравнению с прошлым годом составил 26%.
+: 105
I: {{155}} ТЗ-1-3-27к.
S: Относительный показатель реализации плана по выпуску продукции = ### %, если выпуск продукции по сравнению с базисным годом уменьшился на 4%
а по плану должен был увеличиться на 20%
+: 80
I: {{156}} ТЗ-1-3-28к.
S: Выпуск продукции по сравнению с прошлым годом..., если ОПП=110%, а ОПРП=90%.
+: снизился на 1%
-: увеличился на 1%
-: увеличился на 20%
-: снизился на 20%
-: не изменился
I: {{157}} ТЗ-1-3-29.
S: План реализован на..., если выпуск продукции по сравнению с прошлым годом не изменился, а планировалось его уменьшить на 20%.
+: 125%
-: 25%
-: 20%
-: 120%
-: 100%
I: {{158}} ТЗ-1-3-30.
S: Выпуск продукции в 2004 г. по сравнению с 2002 г. составил ….% (с точностью до 0,1%) при условии:
| Годы | Изменение выпуска |
| в 2003 по сравнению с 2002 г. | увеличился на 10% |
| в 2004 по сравнению с 2003 г. | снизился на 5% |
+: 104,5
-: 105,0
-: 115,0
-: 115,5
I: {{159}} ТЗ-1-3-31.
S: Объем продаж в 2000 г. был равен … млн. руб., если в 2001 г. он вырос по сравнению с 2000 г. на 7% и составил 256,8 млн. руб.
+: 240,0
-: 254,8
-: 274,7
-: 366,9
I: {{160}} ТЗ-1-3-32.
S: Оборот в 2001 г. был равен … млн. руб., если он вырос в 2001 г. по сравнению с 2000 г. на 7%, что составило 28 млн. руб.
+: 428
-: 400
-: 372
-: 566
I: {{161}} ТЗ-1-3-33.
S: Выпущено продукции в 2004 г. больше, чем в 2003 г. на … %, если в 2004 г. выпущено 26 тыс. т, а в 2003 г. 25 тыс. т.
+: 4
-: 3
-: 2
-: 1
I: {{162}} ТЗ-1-3-34.
S: Относительный показатель реализации плана равен …, если в 2004 г. выпущено продукции на 230 млн. руб., что на 20 млн. руб. меньше, чем планировалось.
+: 92 %
-: 9 %
-: 91 %
-: 8 %
I: {{163}} ТЗ-1-3-35.
S: Относительный показатель плана равен …, если в 2005 г. выпущено продукции на 400 млн. руб., а в 2006 г. планируется выпустить продукции на 416 млн. руб.
+: 104 %
-: 96 %
-: 110 %
-: 92 %
I: {{164}} ТЗ-1-3-36.
S: На каждый млн. руб. произведенных продуктов приходится … млн. руб. чистых налогов на продукты, если в 2004 г. произведено продуктов на 320 млн. руб., и собрано чистых налогов на продукты на 50 млн. руб.
+: 0,156
-: 6,400
-: 1,562
-: 5,623
I: {{165}} ТЗ-1-3-37.
S: На 100 безработных мужчин приходится … безработных женщин, если на бирже труда зарегистрировано 256 мужчин и 316 женщин.
+: 123
-: 1,23
-: 81
-: 0,81
I: {{166}} ТЗ-1-3-38.
S: Доля безработных женщин в общей численности безработных равна …, если на бирже труда зарегистрировано 260 мужчин и 240 женщин.
+: 48 %
-: 52 %
-: 49 %
-: 53 %
I: {{167}} ТЗ-1-3-39.
S: Доля безработных женщин в общей численности населения равна ### %, если на бирже труда зарегистрировано 580 женщин, а общая численность населения равна 14500 чел.
+: 4
I: {{168}} ТЗ-1-3-40.
S: Доля импорта в общем товарообороте равна ### %, если импортировано товаров на 25 млрд. руб., а общий товарооборот 500 млрд. руб.
+: 5
I: {{169}} ТЗ-1-3-41.
S: Общий товарооборот равен ### млрд. руб., если импортировано товаров на 24 млрд. руб., а доля импорта в общем товарообороте равна 12 %
+: 200
I: {{170}} ТЗ-1-3-42.
S: Импортировано товаров на ### млрд. руб., если общий товарооборот равен 300 млрд. руб., а доля импорта в общем товарообороте равна 24 %
+: 72
I: {{171}} ТЗ-1-3-1к
S: Относительные величины представляют собой:
-: разность двух статистических величин
-: сумму статистических величин
+: частное от деления двух статистических величин
-: произведение двух статистических величин
I: {{172}} ТЗ-1-3-2к
S: Относительная величина структуры характеризует:
-: развитие явления в определенной среде
+: состав изучаемой совокупности
-: развитие явления во времени
-: соотношение частей совокупности
I: {{173}} ТЗ-1-3-3к
S: Относительная величина структуры определяется как
-: отношение двух разноименных величин;
+: отношение отдельных частей ко всей совокупности;
-: соотношение двух показателей одноименных явлений за разные промежутки или моменты времени;
-: отношение двух одноименных показателей, принадлежащих к одной совокупности;
I: {{174}} ТЗ-1-3-4к
S: Относительный показатель интенсивности представляет собой отношение
-: одной части совокупности к другой части этой же совокупности
-: уровня исследуемого процесса или явления за данный период времени и уровня этого же процесса или явления в прошлом
+ исследуемого показателя к размеру присущей ему среды
-: одного и того же абсолютного показателя, характеризующего разные объекты (предприятия, районы, области, страны)
I: {{175}} ТЗ-1-3-5к
S: Относительные величины представляют собой … двух статистических величин
-: разность
-: сумму
+ частное
-: произведение
I: {{176}} ТЗ-1-3-6к
S: Сумма относительных показателей структуры, рассчитанных по одной совокупности, должна быть
+: строго равной 100
-: меньше или равной 100
-: больше или равной 100
-: меньше, больше или равной 100
I: {{177}} ТЗ-1-3-7к
S: Отношением разноимённых показателей является относительная величина
+: интенсивности
-: динамики
-: структуры
-: пространственного сравнения
I: {{178}} ТЗ-1-3-8к
S: Показатели, характеризующие объёмы и размеры социально-экономических явлений, - это величины
+: абсолютные
-: относительные
-: коэффициенты
-: индексы
I: {{179}} ТЗ-1-3-9к
S: Показатели, характеризующие объёмы и размеры социально-экономических явлений, выражаются единицам измерения
+: натуральными, трудовыми, стоимостными
-: коэффициентами, процентами
-: индексами
-: относительными величинами
V2: {{4}} Тема 4. Средние величины.
I: {{180}} ТЗ-1-4-1п.
S: Средняя величина является обобщающей характеристикой варьирующего признака:
+: в качественно однородной совокупности
-: в любой совокупности
-: в качественно неоднородной совокупности
-: в количественно неоднородной совокупности
I: {{181}} ТЗ-1-4-2п.
S: Значение средней зависит
-: от объема статистической совокупности
-: только от весов индивидуальных значений признака
-: только от индивидуальных значений признака
+: как от индивидуальных значений признака, так и от их весов
I: {{182}} ТЗ-1-4-3-п.
S: Средний балл инвестиционного риска рассчитывается по формуле …, если известны оценки четырех групп экспертов из 5 специалистов каждая.
+: арифметической простой
-: арифметической взвешенной
-: гармонической простой
-: гармонической взвешенной
I: {{183}} ТЗ-1-4-4-п.
S: Средний балл инвестиционного риска рассчитывается по формуле …, если известны оценки четырех разных по численности групп экспертов.
-: арифметической простой
+: арифметической взвешенной
-: гармонической простой
-: гармонической взвешенной
I: {{184}} ТЗ-1-4-5-п.
S: Средний размер налога …, если налог для всех товаропроизводителей увеличен на 3%.
-: не изменится;
+: увеличится на 3%
-: увеличится на 9%
-: увеличится на 6%
I: {{185}} ТЗ-1-4-6п.
S: Общий уровень смертности населения …, если смертность в возрастных группах населения не изменилась, но увеличилась доля лиц старшего возраста во всем населении.
+: увеличился;
-: уменьшился
-: изменение невозможно предсказать.
-: не изменился
I: {{186}} ТЗ-1-4-7п.
S: Средний балл деловой активности предпринимателей равен …, если
| Оценка деловой активности, баллов | Итого | |||
| Число предпринимателей |
-: 2,0;
-: 1,9
+: 2,1
-: 2,2.
I: {{187}} ТЗ-1-4-8п.
S: Средние затраты сырья равны …, если
| Технология производства | Затраты сырья на единицу продукции, т | Всего выпущено продукции, т |
| Старая Новая |
+: 2,6
-: 2,5
-: 2,7
-: 2,8.
I: {{188}} ТЗ-1-4-9.
S: Отношение суммарного значения усредняемого признака к объему совокупности равно
-: вариации значений признака
-: медиане
-: моде
+: среднему значению признака
I: {{189}} ТЗ-1-4-10.
S: Среднее значение признака в несгруппированной совокупности вычисляется по формуле средней...
+: арифметической простой
-: арифметической взвешенной
-: гармонической
-: геометрической
-: хронологической
I: {{190}} ТЗ-1-4-11.
S: Среднее значение признака в группированной совокупности с разными по численности группами вычисляется по формуле средней...
-: арифметической простой
+: арифметической взвешенной
-: гармонической простой
-: гармонической взвешенной
-: геомерической
I: {{191}} ТЗ-1-4-12п.
S: Статистической характеристикой, количественно описывающей закономерность распределения, является
+: средняя
-: вариация
-: асимметрия
-: коэффициент вариации
I: {{192}} ТЗ-1-4-13к.
S: Средняя стоимость произведенной продукции (с точностью до 1 млн. руб.) за 2 квартал = … млн. руб., если
| Месяц | Произведено продукции, млн. руб. |
| апрель | |
| май | |
| июнь |
-: 10
-: 13
+: 12
-: 14
I: {{193}} ТЗ-1-4-14.
S: Средний остаток оборотных средств за второй квартал рассчитывается по формуле средней …. при условии:
| Остатки оборотных средств | млн. руб. |
| На 1 апреля | |
| На 1 мая | |
| На 1 июня | |
| На 1 июля |
-: арифметической
-: гармонической
-: геометрической
+: хронологической
-: квадратической
I: {{194}} ТЗ-1-4-15к.
S: Средняя численность работников (с точностью до 1 чел.) за 2 квартал =### чел., если
| Дата | Численность работников |
| 1 апреля | |
| 1 мая | |
| 1 июня |
+: 23
I: {{195}} ТЗ-1-4-16.
S: Средний стаж работы рассчитывается по формуле средней …, если
| Стаж работы, лет | до 5 | 5 - 10 | 10 - 15 | 15 и более |
| Число рабочих |
-: арифметической простой
+: арифметической взвешенной
-: гармонической простой
-: гармонической взвешенной
-: геомерической
I: {{196}} ТЗ-1-4-17.
S: Расчет средней доли экспортной продукции проводится в форме средней …, если
| Вид продукции | Доля экспортной продукции, % | Стоимость экспортной продукции, тыс. руб. |
| Сталь | ||
| Прокат |
-: арифметической простой
-: арифметической взвешенной
-: гармонической простой
+: гармонической взвешенной
-: хронологической
I: {{197}} ТЗ-1-4-18к.
S: Средний возраст студента равен... лет
| Возраст, лет | ||
| Количество студентов, чел. |
+: 19,6
-: 19,5
-: 19,4
-: 19,3
I: {{198}} ТЗ-1-4-19к.
S: Средний возраст студента равен... лет
| Возраст, лет | 17-19 | 19-21 |
| Количество студентов, чел. |
+: 18,5
-: 19
-: 19,5
-: 20
-: 20,5
I: {{199}} ТЗ-1-4-1к
S: Средняя величина, если все веса уменьшить на некоторую постоянную величину,
-: увеличится
+: не изменится
-: уменьшится на такую же величину
-: изменится непредсказуемым образом
I: {{200}} ТЗ-1-4-2к
S: Степенной средней является
-: средняя арифметическая
-: средняя геометрическая
-: мода
+: средняя квадратическая
-: медиана
I: {{201}} ТЗ-1-4-3к
S: Средняя гармоническая применяется при вычислении среднего значения, если
-: показатели в совокупности прямо пропорциональны
+: показатели обратно пропорциональны, или один из показателей не задан, а выступает как сомножитель в одном из имеющихся в условии
-: при вычислении среднегодового темпа роста в рядах динамики
-: ряд является интервальным
I: {{202}} ТЗ-1-4-4к
S: Средняя заработная плата одного рабочего в бригаде из 5 человек вычисляется по средней …, если
| Фамилия | Андреев | Богданов | Гаврилов | Денисов | Егоров |
| Заработная плата, руб. |
-: арифметической взвешенной
-: гармонической
-: хронологической
+: арифметической простой
I: {{203}} ТЗ-1-4-5к
S: Среднемесячная численность населения за I квартал определяется по средней …, если численность населения приведена на 1.01, 1.02, 1.03 и 1.04.
-: арифметической
-: гармонической
+: хронологической
-: геометрической
I: {{204}} ТЗ-1-4-6к
S: Средняя величина …, если все варианты признака уменьшить в 1,5 раза, а все веса в 1,5 раза увеличить.
-: не изменится
+: уменьшится в 1,5 раза
-: возрастёт в 1,5 раза
-: уменьшится в 3 раза
-: возрастёт в 3 раза
I: {{205}} ТЗ-1-4-7к
S: Средняя величина является обобщающей характеристикой варьирующего признака
+: только в качественно однородной совокупности
-: в любой совокупности
-: в количественно однородной совокупности
-: в совокупности, которая однородна как качественно, так и количественно
I: {{206}} ТЗ-1-4-8к
S: Средняя величина, если все веса уменьшить на 20%,
+: не изменится
-: уменьшится на 20%
-: увеличится на 20%
-: уменьшится на 80%
-: увеличится на 80%
V2: {{5}} Тема 5. Показатели вариации.
I: {{207}} ТЗ-1-5-1п.
S: Мода в ряду распределения — это:
+: наиболее распространенное значение признака
-: наибольшая частота
-: среднее значение признака
-: модуль наибольшего отклонения от средней
I: {{208}} ТЗ-1-5-2п.
S: Мода в дискретном ряду распределения
-: всегда одна
-: может существовать или не существовать
-: не существует
+: может быть одна или несколько
I: {{209}} ТЗ-1-5-3п.
S: Медиана в ряду распределения — это:
-: наиболее распространенное значение признака
+: значение признака, делящее ряд пополам
-: наибольшая частота
-: модуль наибольшего отклонения от средней
I: {{210}} ТЗ-1-5-4п.
S: Медиана в интервальном ряду распределения
+: всегда одна
-: может существовать или не существовать
-: не существует
-: может быть одна или несколько
I: {{211}} ТЗ-1-5-5п.
S: Медиана возраста брокеров равна …, если
| Возраст, лет | Итого | |||||||
| Количество брокеров, чел. |
-: 22
-: 23
+: 24
-: 25
I: {{211}} ТЗ-1-5-6п.
S: Мода числа ошибок, если
| Число ошибок в тесте | Итого | ||||||
| Количество тестов |
равна
-: 1
+: 2
-: 3
-: 4
I: {{212}} ТЗ-1-5-7п.
S: Вариация — это:
+: разнообразие значений определенного признака в статистической совокупности
-: отличия значений разных признаков у отдельного элемента совокупности
-: сумма отклонений значений признака от среднего значения
-: разность между максимальным и минимальным значениями признака в совокупности
I: {{213}} ТЗ-1-5-8п.
S: Вариации в двух совокупностях с одинаковыми средними значениями
-: всегда одинаковы
+: могут быть одинаковыми или разными
-: всегда разные
-: отличаются не более чем на 30%
I: {{214}} ТЗ-1-5-9п.
S: Вариации в двух совокупностях с разными средними значениями
-: всегда одинаковы;
+: могут быть одинаковыми или разными
-: всегда разные
-: отличаются не менее чем на 30%
I: {{215}} ТЗ-1-5-10п.
S: Среднее линейное отклонение вычисляют с помощью … отклонений индивидуальных значений признака от средней.
+: алгебраической суммы
-: суммы абсолютных значений
-: суммы квадратов
I: {{216}} ТЗ-1-5-11п.
S: Среднее линейное и среднее квадратическое отклонения
-: всегда одинаковы
+: иногда могут быть одинаковыми
-: всегда разные
-: всегда одинаковы по абсолютной величине
I: {{217}} ТЗ-1-5-12п.
S: Дисперсия — это … отклонений индивидуальных значений признака от средней.
-: модуль
+: средний квадрат
-: сумма
-: произведение
I: {{218}} ТЗ-1-5-13п.
S: Дисперсию можно определить для признака:
-: только качественного
-: количественного и качественного
-: только для количественного
+: для количественного и альтернативного
I: {{219}} ТЗ-1-5-14п.
S: Если все значения признака увеличить на определенную величину, то дисперсия:
-: увеличится на такую же величину;
-: уменьшится на такую же величину;
+: не изменится;
-: увеличится на квадрат этой величины
I: {{220}} ТЗ-1-5-15п.
S: Коэффициент вариации можно рассчитывать на основе
+: среднеквадратического отклонения
-: среднего линейного отклонения
-: размаха вариации
-: моды
I: {{221}} ТЗ-1-5-16п.
S: Коэффициент вариации используют для сравнения … одного признака в разных совокупностях или разных признаков в одной совокупности
+: вариации
-: среднего значения
-: среднеквадратического отклонения
-: размаха вариации
I: {{222}} ТЗ-1-5-17п.
S: Для измерения вариации групповых средних используют
+: межгрупповую дисперсию
-: групповые дисперсии
-: групповые средние
-: среднее значение признака по всей совокупности
I: {{223}} ТЗ-1-5-18п.
S: Для обобщения вариации индивидуальных значений признака внутри групп используют
-: межгрупповую дисперсию
-: групповые дисперсии
-: общую дисперсию
+: среднюю из групповых дисперсий
I: {{224}} ТЗ-1-5-19к.
S: Для характеристики вариации индивидуальных значений признака в целом по совокупности используют
-: межгрупповую дисперсию
-: групповые дисперсии
+: общую дисперсию
-: среднюю из групповых дисперсий
I: {{225}} ТЗ-1-5-20.
S: Размах вариации вычисляется по формуле
-: R = Хmax - 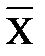
-: R = 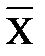 - Хmin
- Хmin
+: R = Хmax - Хmin
-: R = Х - Хmin
I: {{226}} ТЗ-1-5-21.
S: Среднее линейное отклонение вычисляется по формуле
-: 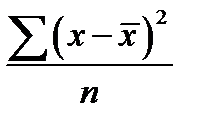
+: 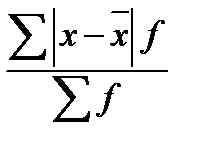
-: 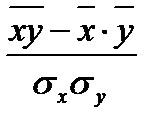
-: 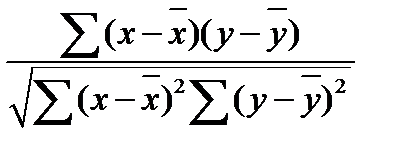
I: {{227}} ТЗ-1-5-22.
S: Дисперсия вычисляется по формуле
-: 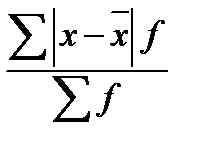
+: 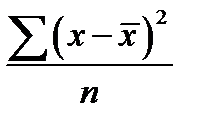
-: 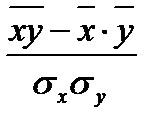
-: 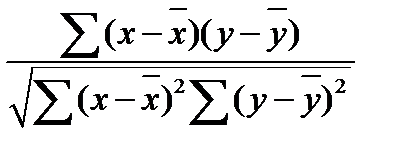
I: {{228}} ТЗ-1-5-23.
S: Дисперсия вычисляется по формуле
-: 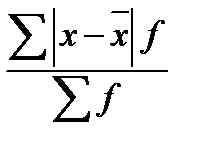
+: 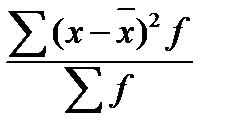
-: 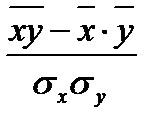
-: 
I: {{229}} ТЗ-1-5-24.
S: Дисперсия вычисляется по формуле
-: 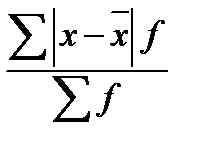
+: 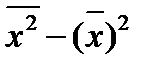
-: 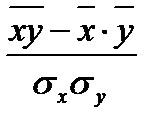
-: 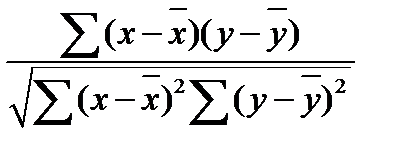
I: {{230}} ТЗ-1-5-25.
S: Среднеквадратическое отклонение вычисляется по формуле
-: 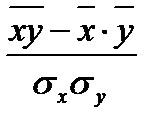
-: 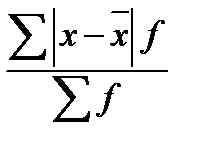
+: 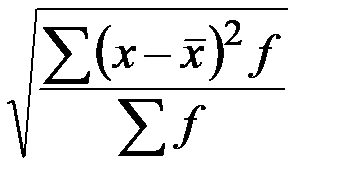
-: 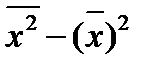
-: 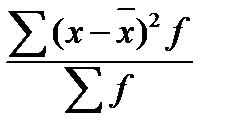
I: {{231}} ТЗ-1-5-26.
S: Коэффициент вариации вычисляется по формуле
-: 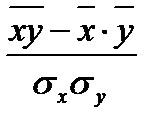
-: 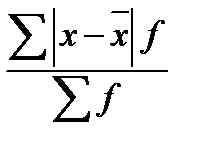
-: 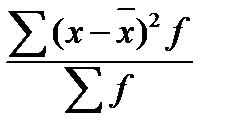
+: 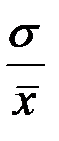
I: {{232}} ТЗ-1-5-27.
S: Относительным показателем вариации является
-: размах вариации
-: дисперсия
+: коэффициент вариации
-: среднее линейное отклонение
I: {{233}} ТЗ-1-5-28.
S: Коэффициент вариации равен
-: отношению дисперсии к средней
-: сумме средней и дисперсии
+: отношению среднеквадратического отклонения к средней
-: сумме среднего линейного отклонения и среднеквадратического отклонения
I: {{234}} ТЗ-1-5-29.
S: Значение признака, наиболее часто встречающееся в совокупности, называется
+: модой
-: медианой
-: вариацией
-: средней
I: {{235}} ТЗ-1-5-30.
S: Общая дисперсия по правилу сложения дисперсий равна
+: сумме межгрупповых дисперсий и средней из внутригрупповых дисперсий
-: разности средней из внутригрупповых дисперсий и межгрупповых дисперсий
-: отношению суммы межгрупповых дисперсий к средней из внутригрупповых дисперсий
I: {{236}} ТЗ-1-5-31к.
S: Дисперсия признака равна ###, если среднее квадратическое отклонение равно 4.
+: 16
I: {{237}} ТЗ-1-5-32к.
S: Среднее квадратическое отклонение признака от средней равно ###, если дисперсия равна 9.
+: 3
I: {{238}} ТЗ-1-5-33к.
S: Коэффициент вариации равен ### % (с точностью до 1%), если дисперсия 9, а средняя 5.
+: 60
I: {{239}} ТЗ-1-5-34к.
S: Среднее квадратическое отклонение признака от средней равно ### (с точностью до 1), если коэффициент вариации равен 20%, а средняя 15.
+: 3
I: {{240}} ТЗ-1-5-35к.
S: Дисперсия равна ### (с точностью до 1), если коэффициент вариации равен 20%, а средняя 15.
+: 9
I: {{241}} ТЗ-1-5-36.
S: Мода равна... для значений признака: 3, 3, 3, 5, 5, 6, 9, 11, 12, 13
+: 3
-: 5
-: 6
-: 9
-: 11
-: 12
-: 13
I: {{242}} ТЗ-1-5-37.
S: Мода равна... для значений признака: 3, 3, 4, 4, 6, 6, 6, 7, 9, 9
-: 3
-: 4
+: 6
-: 7
-: 9
I: {{243}} ТЗ-1-5-38к.
S: Мода рейтинга студентов = ### баллов (с точностью до 1 балла), если
| Рейтинг | Число студентов |
+: 7
I: {{244}} ТЗ-1-5-39к.
S: Медиана рейтинга студентов = ### баллов (с точностью до 1 балла), если
| Рейтинг | Число студентов |
| Итого |
+: 7
I: {{245}} ТЗ-1-5-40.
S: Медиана в ряду распределения рабочих по уровню заработной платы равна 12 тыс. руб., следовательно...
-: среднее значение заработной платы в данном ряду распределения равно 12 тыс. руб.
-: наиболее часто встречающееся значение заработной платы в данном ряду распределения равно 12 тыс. руб.
+: 50% рабочих имеют заработную плату не более 12 тыс. руб.
I: {{246}} ТЗ-1-5-41.
S: Дисперсия признака = ### (с точностью до 1), если средняя величина признака 20, коэффициент вариации 25%.
+: 25
I: {{247}} ТЗ-1-5-42.
S: Среднеквадратическое отклонение признака = ### (с точностью до 1), если средняя величина признака 300, коэффициент вариации 27%.
+: 81
I: {{248}} ТЗ-1-5-43.
S: Модальным интервалом ряда распределения является интервал …
| Жилая площадь, кв. м / чел. | 3 - 5 | 5 - 7 | 7 - 9 | 9 - 11 | 11 и более |
| Число семей |
-: от 3 до 5
-: от 5 до 7
-: от 7 до 11
+: от 9 до 11
-: 11 и более
I: {{249}} ТЗ-1-5-44.
S: Медианным интервалом ряда распределения является интервал …
| Жилая площадь, кв. м / чел. | 3 - 5 | 5 - 7 | 7 - 9 | 9 - 11 | 11 и более | Итого |
| Число семей |
-: от 5 до 7
-: от 3 до 5
+: от 7 до 9
-: от 9 до 11
-: 11 и более
I: {{250}} ТЗ-1-5-45к.
S: Коэффициент вариации =### % (с точностью до 1%), если средняя величина признака 30, среднеквадратическое отклонение 9
+: 30
I: {{251}} ТЗ-1-5-1к
S: Показателем вариации, имеющим ту же размерность, что и признаки изучаемой статистической совокупности, является
-: дисперсия
+: среднеквадратическое отклонение
-: коэффициент вариации
-: коэффициент корреляции
I: {{252}} ТЗ-1-5-2к
S: Показателем вариации, имеющим ту же размерность, что и признаки изучаемой статистической совокупности, является
-: дисперсия
-: коэффициент вариации
+: среднее линейное отклонение
-: коэффициент корреляции
I: {{253}} ТЗ-1-5-3к
S: Вариация характеризует:
-: среднюю величину совокупности
+: колеблемость отдельных значений признака относительно средней
-: варианту, наиболее часто встречающуюся в совокупности
-: однородность совокупности
I: {{254}} ТЗ-1-5-4к
S: Структура ряда распределения значений признака характеризуется
-: средней арифметической
-: средней геометрической
-: средней кубической
+: модой
I: {{255}} ТЗ-1-5-5к
S: Абсолютным показателем вариации является
+: размах вариации
-: дисперсия
-: коэффициент вариации
-: коэффициент осцилляции
I: {{256}} ТЗ-1-5-6к
S: Структурной средней является
-: средняя арифметическая
-: средняя геометрическая
-: средняя кубическая
-: средняя гармоническая
+: медиана
I: {{257}} ТЗ-1-5-7к
S: Коэффициент вариации характеризует
-: диапазон вариации признака
+: степень вариации признака
-: тесноту связи между признаками
-: пределы колеблемости признака
I: {{258}} ТЗ-1-5-8к
S: Вариация в совокупностях с одинаковыми средними значениями
+: может быть как разной, так и одинаковой
-: всегда одинаковая
-: всегда разная
-: одинаковая в однородных совокупностях
I: {{259}} ТЗ-1-5-9к
S: Вариация в совокупностях с разными средними значениями
+: может быть как разной, так и одинаковой
-: всегда одинаковая
-: всегда разная
-: одинакова в однородных совокупностях
I: {{260}} ТЗ-1-5-10к
S: Значение медианы в ряду распределения совпадает со значением средней для … распределения
+: симметричного
-: асимметричного
-: любого симметричного и асимметричного
-: однородного
I: {{261}} ТЗ-1-5-11к
S: Коэффициент вариации рассчитывается с помощью среднего значения признака и
+: среднего квадратического отклонения
-: среднего линейного отклонения
-: вариационного размаха
-: дисперсии
I: {{262}} ТЗ-1-5-12к
S: Дисперсию можно определить
-: только для количественного признака
+: для количественного и альтернативного признака
-: только для качественного признака
-: для качественного и количественного признаков
V2: {{6}} Тема 6. Индексы.
I: {{263}} ТЗ-1-6-1.
S: Весами в агрегатном индексе физического объема продукции являются
-: цены текущего периода
+: цены базисного периода
-: объем товарооборота текущего периода
-: объем товарооборота базисного периода
I: {{264}} ТЗ-1-6-2.
S: Весами в агрегатном индексе цен являются
+: физический объем продукции текущего периода
-: физический объем продукции базисного периода
-: объем товарооборота текущего периода
-: объем товарооборота базисного периода
I: {{265}} ТЗ-1-6-3.
S: Индекс цен равен
+: отношению индекса товарооборота к индексу физического объема продукции
-: сумме индексов товарооборота и физического объема продукции
-: отношению индекса физического объема продукции к индексу товарооборота
-: произведению индекса товарооборота и индекса физического объема продукции
I: {{266}} ТЗ-1-6-4.
S: Связь между сводными индексами товарооборота (Ipq), физического объема продукции (Iq) и цен (Ip) выражается формулой
-: Iq = Iрq ´ Ip
-: Ip = Iq ´ Iрq
+: Iрq = Iq ´ Ip
-: Iрq = Iq : Ip
I: {{267}} ТЗ-1-6-5.
S: Связь между сводными индексами издержек производства (Izq), физического объема продукции (Iq) и себестоимости (Iz ) выражается формулой
-: Iq = Izq ´ Iz
-: Iz = Iq ´ Izq
+: Izq = Iq ´ Iz
-: Izq = Iq : Iz
I: {{268}} ТЗ-1-6-6.
S: Весами в агрегатных индексах качественных показателей являются показатели
+: отчетного периода
-: базисного периода
I: {{269}} ТЗ-1-6-7.
S: Весами в агрегатных индексах количественных показателей являются показатели
-: отчетного периода
+: базисного периода
I: {{270}} ТЗ-1-6-8к.
S: Весами в среднем гармоническом индексе цен являются
-: товарооборот базисного периода
+: товарооборот отчетного периода
-: физический объем базисного периода
-: физический объем отчетного периода
I: {{271}} ТЗ-1-6-9к.
S: Весами в среднем арифметическом индексе физического объема являются
+: товарооборот базисного периода
-: товарооборот отчетного периода
-: цены базисного периода
-: цены отчетного периода
I: {{272}} ТЗ-1-6-10к.
S: Цена в отчетном периоде..., чем в базисном, если индекс цен 1,25.
+: больше на 25%
-: меньше на 25%
-: больше на 125%
-: меньше на 125%
-: больше на 20%
-: меньше на 20%
I: {{273}} ТЗ-1-6-11к.
S: Покупательная способность рубля в отчетном периоде меньше, чем в базисном на ### % (с точностью до 1%) если индекс цен 1,25
+: 20
I: {{274}} ТЗ-1-6-12к.
S: Индекс цен равен ### % (с точностью до 0,01) если цена в отчетном периоде больше, чем в базисном на 7%
+: 1,07
+: 1.07
I: {{275}} ТЗ-1-6-13к.
S: Цена в отчетном периоде меньше, чем в базисном на ### % (с точностью до 1%), если индекс покупательной способности рубля 1,25
+: 20
I: {{276}} ТЗ-1-6-14к.
S: В отчетном периоде произведено продукции..., чем в базисном, если индекс физического объема 1,05 на
+: 5% больше
-: 5% меньше
-: 50% больше
-: 50% меньше
I: {{277}} ТЗ-1-6-15к.
S: Цена ДСП в ноябре по сравнению с сентябрем увеличилась на ### % (с точностью до 1%) если известно, что в октябре она была больше, чем в сентябре на 20%, а в ноябре меньше, чем в октябре на 5%
+: 14
I: {{278}} ТЗ-1-6-16к.
S: Себестоимость продукции уменьшилась на = ### % (с точностью до 1%), если объем выпускаемой продукции увеличился на 20%, а индекс затрат равен 1,14.
+: 5
I: {{279}} ТЗ-1-6-17к.
S: Объем произведенной продукции увеличился на ### % (с точностью до 1%), если товарооборот вырос на 38%, а индекс цен равен 1,15
+: 20
I: {{280}} ТЗ-1-6-18к.
S: Товарооборот уменьшился на ### % (с точностью до 1%), если физический объем продукции не изменился, а индекс цен равен 0,98,
+: 2
I: {{281}} ТЗ-1-6-19к.
S: Производственные затраты увеличились на ### % (с точностью до 1%), если себестоимость единицы продукции увеличилась на 20%, а индекс физического объема 1,1.
+: 32
I: {{282}} ТЗ-1-6-20к.
S: Себестоимость в ноябре по сравнению с сентябрем увеличилась на ### % (с точностью до 1%) если известно, что в октябре она была меньше, чем в сентябре на 20%, а в ноябре меньше, чем в октябре на 15%
+: 68
I: {{283}} ТЗ-1-6-21к.
S: Средняя выработка продукции в расчете на одного рабочего увеличилась на = ### % (с точностью до 1%), если объем выпускаемой продукции увеличился на 2%, а индекс численности рабочих равен 0,75.
+: 36
I: {{284}} ТЗ-1-6-22к.
S: Численность рабочих увеличилась на ### % (с точностью до 1%), если средняя выработка продукции в расчете на одного рабочего возросла на 25%, а индекс объема выпуска продукции равен 1,3
+: 4
I: {{285}} ТЗ-1-6-23к.
S: Себестоимости единицы продукции увеличилась на ### % (с точностью до 1%), если физический объем продукции снизился на 20%, а индекс производственных затрат равен 1,08,
+: 35
I: {{286}} ТЗ-1-6-24к.
S: Производственные затраты сократились на ### % (с точностью до 1%), если индекс себестоимости единицы продукции 0,9, а физического объема 1,1.
+: 1
I: {{287}} ТЗ-1-6-25к.
S: Индекс физического объема продукции по предприятию в целом = ### (с точностью до 0,1), если
| Вид продукции | Количество продукции, т | Цена, тыс. руб. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| А Б |
+: 2,3
+: 2.3
I: {{288}} ТЗ-1-6-26к.
S: Индекс цен переменного состава = …. (с точностью до 0,01), если
| Поставщик | Цена, руб. | Объем продаж, кг | ||
| январь | февраль | январь | февраль | |
| А Б |
+: 0,92
+: 0.92
I: {{289}} ТЗ-1-6-27к.
S: Индекс цен постоянного состава = …. (с точностью до 0,01), если
| Поставщик | Цена, руб. | Объем продаж, кг | ||
| январь | февраль | январь | февраль | |
| А Б |
+: 0,97
+: 0.97
I: {{290}} ТЗ-1-6-28.
S: Индекс переменного состава вычисляют по формуле:
+: 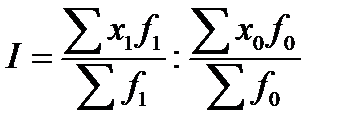
-: 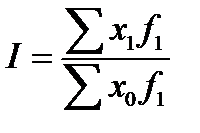
-: 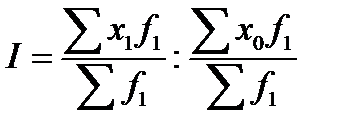
-: 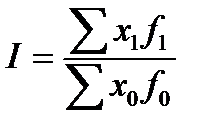
-: 
I: {{300}} ТЗ-1-6-29.
S: Индекс постоянного состава вычисляют по формуле:
-: 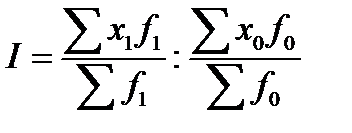
+: 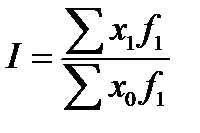
-: 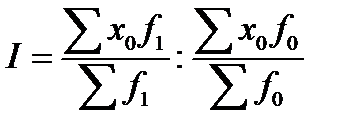
I: {{301}} ТЗ-1-6-30.
S: Индекс структурных сдвигов вычисляют по формуле:
-: 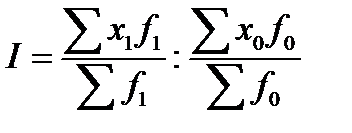
-: 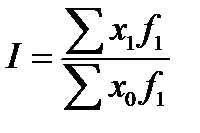
-: 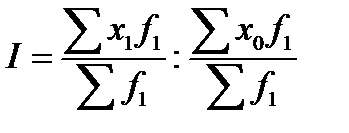
+: 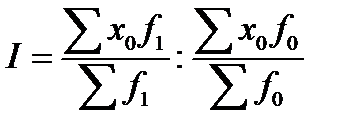
I: {{302}} ТЗ-1-6-31.
S: Связь между индексами переменного Iпер.сост., постоянного составов Iпост.сост и структурных сдвигов Iстр.сд определяется как:
+: Iпер.сост. = Iпост.сост ´ Iстр.сд.
-: Iпер.сост. = Iпост.сост: Iстр.сд.
-: Iпост.сост. = Iпер.сост ´ Iстр.сд.
-: Iстр.сд. = Iпост.сост ´ Iпер.сост.
I: {{303}} ТЗ-1-6-32к.
S: Индекс цен переменного состава равен..., если индекс структурных сдвигов 1,20, а индекс переменного состава 1,05.
+: 1,26
-: 1,25
-: 1,14
-: 0,88
I: {{304}} ТЗ-1-6-33к.
S: За счет структурных сдвигов цены..., если индекс цен переменного состава равен 1,4, индекс постоянного состава 1,25.
+: выросли на 12%
-: снизились на 12%
-: выросли на 5%
-: снизились на 5%
-: выросли на 75%
-: снизились на 75%
I: {{305}} ТЗ-1-6-34к.
S: Физический объем продукции в текущем периоде по сравнению с базисным …, если товарооборот увеличился на 10% и цены увеличились на 10%
-: уменьшился на 21%
-: увеличился на 20%
-: уменьшился на 20%
-: увеличился на 21%
+: не изменился
I: {{306}} ТЗ-1-6-35к.
S: Товарооборот в текущем периоде по сравнению с базисным …, если физический объем продукции увеличился на 10% и цены увеличились на 10%
-: уменьшился на 21%
+: увеличился на 20%
-: уменьшился на 20%
-: увеличился на 21%
-: не изменился
I: {{307}} ТЗ-1-6-36к.
S: Цены в текущем периоде по сравнению с базисным …, если физический объем продукции увеличился на 20% и товарооборот увеличился на 20%
-: уменьшились на 21%
-: увеличились на 20%
-: уменьшились на 20%
-: увеличились на 21%
+: не изменились
I: {{308}} ТЗ-1-6-37к.
S: Физический объем продукции в 2004 г. по сравнению с 2002 г. увеличился на …% (с точностью до 1%), если физический объем продукции
- в 2003 г. по сравнению с 2002 г. увеличился на 15%
- в 2004 г. по сравнению с 2003 г. уменьшился на 20%
+: 8
I: {{309}} ТЗ-1-6-38к.
S: Индекс физического объема продукции равен …, если затраты на выпуск продукции в отчетном периоде по сравнению с базисным увеличились на 12%, себестоимость единицы продукции снизилась на 20%.
+: 1,4
-: 0,92
-: 1,32
-: 0,9
I: {{310}} ТЗ-1-6-1к
S: Индексы, которые применяются в статистическом анализе, характеризуют
-: структуру совокупности
+: изменение простого или сложного явления, состоящего из соизмеримых или несоизмеримых элементов
-: тесноту связи показателей в статистической совокупности
-: зависимость показателей в статистической совокупности
I: {{311}} ТЗ-1-6-2к
S: Среднеарифметический и среднегармонический индексы тождественны
-: индивидуальным индексам
+: агрегатным индексам постоянного состава
-: индексам структурных сдвигов
-: индексам переменного состава
I: {{312}} ТЗ-1-6-3к
S: Товарооборот в результате повышения цен в отчетном периоде по сравнению с базисным, при условии, что количество проданных товаров останется прежним,
+: повысится
-: не изменится
-: снизится
-: изменится непредсказуемым образом
I: {{313}} ТЗ-1-6-4к
S: Индексы-дефляторы представляют собой
-: индексы физического объема, характеризующие изменение объема продукции
+: индексы цен, используемые для пересчета показателей, выраженных в текущих ценах в сопоставимые цены
-: индексы, характеризующие изменение затрат на производство продукции
-: индексы товарооборота
I: {{314}} ТЗ-1-6-5к
S: Система взаимосвязанных индексов переменного и постоянного состава и структурных сдвигов применяется в исследовании динамики средней себестоимости или средней цены
+: однородной продукции, которая производится или продается на отдельных объектах
-: разнородной продукции, которая не поддается суммированию в натурально-вещественной форме
-: однородной продукции, которая не поддается суммированию в натурально-вещественной форме
-: одинаковой продукции, произведенным одним и тем же предприятием
I: {{315}} ТЗ-1-6-6к
S: Индекс переменного состава характеризует изменение среднего уровня какого-либо явления за счет
-: одного фактора
+: двух факторов
-: трех факторов
-: четырех факторов
I: {{316}} ТЗ-1-6-7к
S: Индекс постоянного состава характеризует изменение среднего уровня явления за счет
-: только изменения структуры совокупности
+: только изменения уровня явления по каждому элементу изучаемой совокупности
-: изменения как структуры совокупности, так и изменения уровня явления по каждому элементу изучаемой совокупности
I: {{317}} ТЗ-1-6-8к
S: Индекс себестоимости продукции показывает, во сколько раз
-: изменилась стоимость продукции в результате изменения объема ее производства
-: возросли (уменьшились) издержки производства продукции
-: изменились издержки производства продукции в результате изменения объема ее производства
+: изменились издержки производства продукции в результате изменения себестоимости продукции
I: {{318}} ТЗ-1-6-9к
S: Разность числителя и знаменателя индекса товарооборота показывает (в денежном выражении) изменение стоимости продукции
+: в текущем периоде по сравнению с базисным
-: в результате изменения цен
-: в результате изменения объема ее производства
-: в результате изменения издержек производства
I: {{319}} ТЗ-1-6-10к
S: Индекс инфляции при увеличении цен на 25% составит
+: 80
-: 78
-: 75,1
-: 85
I: {{320}} ТЗ-1-6-11к
S: Индекс инфляции и индекс цен находятся в … отношении
-: прямом
+: обратном
-: квадратическом
-: экспоненциальном
I: {{321}} ТЗ-1-6-12к
S: Индекс инфляции, если цены возросли на 30%, равен
-: 0,800
+: 0,769
-: 0,750
-: 0,850
I: {{322}} ТЗ-1-6-13к
S: Весом в общем индексе физического объема является
-: цена товара в отчетном периоде
+: цена товара в базисном периоде
-: себестоимость товара в базисном периоде
-: трудоемкость в базисном периоде
I: {{323}} ТЗ-1-6-14
S: Индекс переменного состава - это
+: отношение двух взвешенных средних с изменяющимися весами
-: среднее изменение индексируемой величины
-: показатель влияния структурных сдвигов на исследуемый средний показатель
-: отношение двух взвешенных средних с одинаковыми весами
I: {{324}} ТЗ-1-6-15к
S: Индексами средних величин являются
-: индивидуальные
-: индексы количественных показателей
-: индексы качественных показателей
-: средневзвешенные
+: переменного состава
-: постоянного состава
-: индексы структурных сдвигов
I: {{325}} ТЗ-1-6-16к
S: Индексы делятся по содержанию изучаемых объектов на
+: индивидуальные и общие
-: индексы количественных и качественных показателей
-: агрегатные и средневзвешенные
-: переменного, постоянного состава и структурных сдвигов
I: {{326}} ТЗ-1-6-17к
S: Индекс постоянного состава
-: это отношение двух взвешенных средних с изменяющимися весами
+: показывает, во сколько раз в среднем изменилась индексируемая величина
-: показывает влияние структурных сдвигов на исследуемый средний показатель
-: отношение объектов произведенной продукции
I: {{327}} ТЗ-1-6-18к
S: Индекс в статистике - это
-: абсолютная величина
+: относительный показатель
-: средняя величина
-: показатель вариации
V2: {{7}} Тема 7. Ряды динамики
I: {{328}} ТЗ-1-7-1.
S: Ряд динамики характеризует:
-: структуру совокупности по какому-либо признаку
+: изменение значений признака во времени
-: определенное значение варьирующего признака в совокупности
-: факторы изменения показателя на определенную дату или за определенный период
I: {{329}} ТЗ-1-7-2.
S: Моментным рядом динамики является
+: остаток оборотных средств предприятия по состоянию на 1 число каждого месяца
-: производительность труда на предприятии за каждый месяц года
-: средняя заработная плата рабочих и служащих по месяцам года
I: {{330}} ТЗ-1-7-3к.
S: Абсолютный цепной прирост исчисляется по формуле
-: 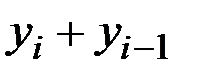
+: 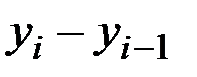
-: 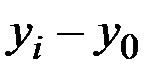
-: 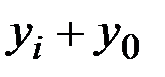
I: {{331}} ТЗ-1-7-4к.
S: Базисный темп роста исчисляется по формуле
-: 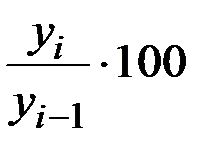
+: 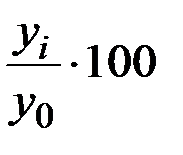
-: 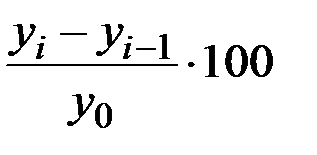
-: 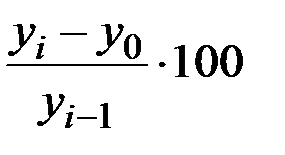
I: {{332}} ТЗ-1-7-5к.
S: Цепной темп прироста исчисляется по формуле
+: Трц– 100
-: Трб– 100
-: 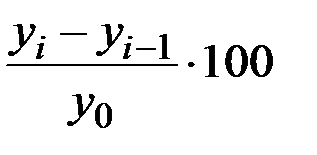
-: 
I: {{333}} ТЗ-1-7-6к.
S: Абсолютное значение 1% прироста исчисляется по формуле
-: 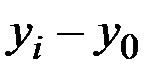
+: 0,01× yi-1
-: 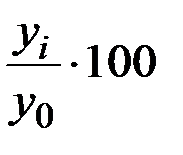
-: 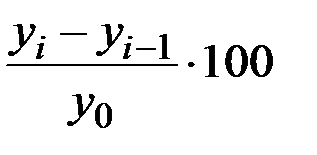
I: {{334}} ТЗ-1-7-7.
S: По формуле 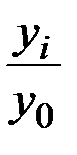 определяется
определяется
+: базисный темп роста
-: цепной темп роста
-: базисный темп прироста
-: цепной темп прироста
-: абсолютное значение 1% прироста
I: {{335}} ТЗ-1-7-8.
S: По формуле 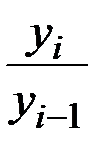 определяется
определяется
-: базисный темп роста
+: цепной темп роста
-: базисный темп прироста
Date: 2015-09-26; view: 1676; Нарушение авторских прав