Глоссарий по дисциплине

Алгоритм - полностью определенный, конечный набор шагов, операций или процедур, которые приводят к конкретному результату.

Альтернативная вариация – простейший случай качественной вариации, когда совокупность состоит только из двух групп: одной, имеющий данный признак, а другой – его не имеющий.

Анализ выживаемости - (разведочный анализ данных и проверка гипотез) включает описательные методы для оценивания распределения выборочных времен жизни, сравнения выживаемости в двух или нескольких группах, а также опции подгонки линейных и нелинейных регрессионных моделей к данным о выживаемости. Характерным аспектом данных о выживаемости является наличие так называемых цензурированных наблюдений, например, наблюдаемых объектов, которые дожили до определенного момента времени, а после этого были исключены из наблюдения. Вместо удаления такого наблюдения из множества изучаемых данных (т.е. необязательной потери потенциально важной информации), методы анализа выживаемости позволяют собрать цензурированные наблюдения и использовать их при проверке статистической значимости и подгонке модели.

Анализ соответствий - это раздел статистики, разрабатывающий описательные/разведочные методы анализа двухвходовых и многовходовых таблиц, которые обуславливают некоторую степень соответствия между строками и столбцами. Результаты этих методов похожи по своей природе на методы факторного анализа и позволяют исследовать структуру группирующих переменных, включенных в таблицу.

Аппарат Гальтона – устройство, предназначенное для наглядной демонстрации распределения вариант в виде вариационного ряда, частоты в котором следуют коэффициентам разложения бинома Ньютона.

Апостериорные сравнения - Обычно, получив при проведении дисперсионного анализа статистически значимое значение F-критерия, мы хотели бы узнать, какая из групп вызвала этот эффект, т.е. какие из групп значительно отличаются от других. Конечно, мы могли бы вычислить последовательность обычных t-критериев для сравнения всех возможных пар средних. Однако такая процедура будет основана на случайности. Получаемые уровни вероятности будут завышать значимость различия между средними. Например, предположим, что мы получили 20 выборок по 10 случайно выбранных чисел каждая, а затем вычислили 20 средних. После этого возьмем группу (выборку) с наибольшим средним и сравнить ее с выборкой с наименьшим средним. t-критерий для независимых выборок проверяет, являются ли два средних значимо отличающимися друг от друга, в предположении, что рассматриваются всего две выборки. Метод апостериорных сравнений, наоборот, предполагает наличие более чем двух выборок. Этот метод используется для проверки гипотез и разведочного анализа.

Априорные вероятности - задают пропорции классов в популяции (в задачах классификации), особенно в тех случаях, когда известно, что эти пропорции отличаются от пропорций в обучающем множестве. Используются для модификации обучения.

Асимметрия или коэффициент асимметрии - (термин был впервые введен Пирсоном, 1895) является мерой несимметричности распределения. Если этот коэффициент отчетливо отличается от 0, распределение является асимметричным. Плотность нормального распределения симметрична относительно среднего.

Байесовы сети - сети, чей принцип действия основан на теореме Байеса, позволяющей сделать выводы о распределении вероятностей на основании имеющихся данных.

Бимодальное распределение - распределение, имеющее две моды (т.е. два "пика"). Бимодальность распределения выборки часто является показателем того, что распределение не является нормальным. Б.Р. дает важную информацию о природе исследуемой переменной. Например, если переменная представляет собой предпочтение или отношение к чему-то, то бимодальность может означать противоположность мнений. Тем не менее, бимодальность часто может показывать, что выборка не является однородной и наблюдения порождены двумя или более "наложенными" распределениями. Иногда бимодальность распределения означает, что выбранные инструменты не подходят для измерения.

Биноминальное распределение – распределение, при котором вероятности появления отдельных значений x_i выражаются величинами, соответствующие коэффициентам разложения бинома Ньютона.

Варианта – значение или мера признака для единицы совокупности.

Варианса (средний квадрат отклонений вариант от средней арифметической) 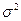– это сумма квадратов отклонений отдельных значений данной переменной от средней арифметической, деленная на число вариант.

Вариация (дисперсия) - различие между единицами совокупности.

Вариационный ряд – ряд, в котором показано, как часто встречаются варианты каждого класса и как варьируют признаки от минимальной величины до максимальной.

Вероятность – возможность осуществления определенного события в некотором количестве случаев из общего числа возможных, или, иначе говоря, степень уверенности в том, что событие произойдет.

Вероятностный или стохастический процесс – процесс осуществления явления на основе известной его возможности или вероятности.

Вероятностные нейронные сети - в ид нейронных сетей для задач классификации, где плотность вероятности принадлежности классам оценивается посредством ядерной аппроксимации.

Взаимодействия - эффект взаимодействия возникает, когда зависимость между двумя или более переменными изменяется под воздействием одной или нескольких других переменных. Другими словами, сила или знак (направление взаимодействия) зависимости между двумя или более переменными зависит от значения принимаемого некоторыми другими переменными. Термин взаимодействие был впервые использован в работе Фишера (Fisher, 1926). Отметим, что слово "зависит" в данном контексте не означает причинной зависимости, а просто отражает тот факт, что в зависимости от рассматриваемого подмножества наблюдений (от значения модифицирующей переменной или переменных) характер зависимости будет меняться (модифицироваться).

Внутриклассовый коэффициент корреляции - значение внутриклассового коэффициента корреляции для популяции является мерой однородности наблюдений внутри классов случайного фактора относительно изменчивости наблюдений между классами. Он равен нулю только в случае, когда оцениваемый эффект случайного фактора равен нулю, и достигает единицы только если оцениваемый эффект ошибки равен нулю, при условии, что общая дисперсия наблюдений отлична от нуля. В нутриклассовый коэффициент корреляции может быть измерен с помощью метода оценивания компонент дисперсии.

Временной ряд - это последовательность измерений в последовательные моменты времени. Анализ временных рядов включает широкий спектр разведочных процедур и исследовательских методов, которые ставят две основные цели: (a) определение природы временного ряда и (b) прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям). Обе эти цели требуют, чтобы модель ряда была идентифицирована и, более или менее, формально описана. Как только модель определена, вы можете с ее помощью интерпретировать рассматриваемые данные (например, использовать в вашей теории для понимания сезонного изменения цен на товары, если занимаетесь экономикой). Не обращая внимания на глубину понимания и справедливость теории, вы можете экстраполировать затем ряд на основе найденной модели, т.е. предсказать его будущие значения.

Выбросы - это нетипичные или редкие значения, которые существенно отклоняются от распределения остальных выборочных данных. Эти данные могут отражать истинные свойства изучаемого явления (переменной), а могут быть связаны с ошибками измерения или аномальными явлениями, и поэтому не должны включаться в модель.

Выборочная совокупность – сравнительно небольшая по объему совокупность, входящая в состав генеральной.

Генеральная совокупность – теоретически бесконечно большая или приближающаяся к бесконечности совокупность.

Групповое программное обеспечение - это программное обеспечение, которое дает возможность группе пользователей, использующих компьютерную сеть, одновременно работать над конкретным проектом. Оно содержит средства для организации связи (электронную почту), для совместной обработки документов, проведения анализа, создания отчетов и статистической обработки данных, а также календарного планирования и наблюдения. При этом обрабатываемые документы могут содержать информацию любого типа: текст, картинки или мультимедийный формат. Дискриминантный анализ - используется для принятия решения о том, какие переменные дискриминируют или разделяют объекты на две или более естественно возникающих групп (его используют как метод проверки гипотез или как метод разведочного анализа).

Дисперсионный анализ – позволяет оценивать значимость влияния отдельных факторов, а также их относительную роль в общей изменчивости. Д. а. был разработан английским математиком и биологом Р. Фишером.

Доверительные вероятности – вероятность, при достижении которой можно с большой степенью уверенности заключить определенный вывод. В биологии используются доверительные вероятности: 0,95 и 0,99. Понятие Д.В. было введено Р. Фишером.

Доверительные границы или доверительный интервал - используются для оценки той или иной величины, указывают те границы, в которых она может находиться при разных вероятностях.

Доля выборки – отношение n/N, где n – численность выборочной совокупности, а N – численность генеральной совокупности. Используется для получения более точного значения средней ошибки.

Желаемая точность – допустимое расхождение между средней арифметической (по данному признаку) выборки и средней арифметической генеральной совокупности.

Закон больших чисел – выражает связь между статистическими показателями выборочных и генеральных совокупностей, заключается в том, что чем больше число n некоторых случайных величин, тем их средняя арифметическая ближе к средней арифметической генеральной совокупности.

Интервальная шкала -эта шкала измерений позволяет не только упорядочить наблюдения, но и количественно выразить расстояния между ними (при этом на шкале не обязательно присутствует абсолютная нулевая отметка).

Интерполяция - восстановление значения функции в промежуточной точке по известным ее значениям в соседних точках.

Канонический анализ - каноническая корреляция позволяет исследовать зависимость между двумя наборами переменных (и применяется для проверки гипотез или как метод разведочного анализа).

Категоризация, группировка, разбиение на подмножества - одним из наиболее важных, общих, а также мощных аналитических методов заключается в разделении (разбиении) данных на несколько подмножеств и последующее сравнение структуры данных в полученных подмножествах. У этого общего метода имеется много различных названий (в том числе: разбиение, группировка, категоризация, расщепление, разветвление и условный анализ), и он используется как для разведочного анализа данных, так и для проверки гипотез.

Качественная изменчивость – изменчивость, различия между вариантами которой выражаются в каких-либо качествах.

Классификация - отнесение наблюдения к одному из нескольких, заранее известных классов (представленных значениями номинальной выходной переменной).

Кластерный анализ - термин кластерный анализ (впервые ввел Tryon, 1939) в действительности включает в себя набор различных алгоритмов классификации. Общий вопрос, задаваемый исследователями во многих областях, состоит в том, как организовать наблюдаемые данные в наглядные структуры, т.е. развернуть таксономии и определить кластеры схожих объектов. Например, биологи ставят цель разбить животных на различные виды, чтобы содержательно описать различия между ними. В соответствии с современной системой, принятой в биологии, человек принадлежит к приматам, млекопитающим, амниотам, позвоночным и животным. Заметьте, что в этой классификации, чем выше уровень агрегации, тем меньше сходства между членами в соответствующем классе. Человек имеет больше сходства с другими приматами (т.е. с обезьянами), чем с "отдаленными" членами семейства млекопитающих (например, собаками) и т.д.

Ковариация - показатель, являющийся связующим звеном между корреляционным и регрессионным методами анализа.

Коды (значения группирующих переменных) - представляют собой значения группирующей переменной (например, 1, 2, 3,... или Мужской, Женский), которые определяют уровни группирующей переменной для анализа. Коды могут быть как целочисленными, так и текстовыми значениями.

Количественная дискретная (прерывная) изменчивость – изменчивость, при которой различия между вариантами отдельными значениями случайной переменной, выражаются целыми числами, между которыми нет и не может быть переходов.

Количественная непрерывная изменчивость – вариация, при которой значения вариант выражаются как целыми, так и дробными числами.

Комплексные числа - это множество чисел, которое включает все действительные и мнимые числа. Комплексное число представляется выражением вида a + ib, где a и b - действительные числа, i - мнимая единица,

Компоненты дисперсии (в смешанной модели дисперсионного анализа). Термин компоненты дисперсии используется в контексте дисперсионного анализа и планирования эксперимента, включающего случайные эффекты, для обозначения оценки (доли) дисперсии, которая связана с этими эффектами.

Корреляция - это мера связи между двумя переменными. Коэффициент корреляции может изменяться от -1.00 до +1.00. Значение -1.00 означает полностью отрицательную корреляцию, значение +1.00 означает полностью положительную корреляцию. Значение 0.00 означает отсутствие корреляции.

Корреляция Пирсона - наиболее часто используемый коэффициент корреляции Пирсона r (Pearson, 1896) называется также линейной корреляцией (термин корреляция впервые ввел Galton, 1888), т.к. измеряет степень линейных связей между переменными. Можно сказать, что корреляция определяет степень, с которой значения двух переменных пропорциональны друг другу. Важно, что значение коэффициента корреляции не зависит от масштаба измерения. Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения в дюймах и фунтах или в сантиметрах и килограммах. Пропорциональность означает просто линейную зависимость. Корреляция высокая, если на графике зависимость можно представить прямой линией (с положительным или отрицательным углом наклона). Проведенная прямая называется прямой регрессии или прямой, построенной методом наименьших квадратов. Последний термин связан с тем, что сумма квадратов расстояний (вычисленная по оси Y) от наблюдаемых точек до прямой является минимальной из всех возможных. Заметим, что использование квадратов расстояний приводит к тому, что на оценки параметров сильно влияют выбросы. Корреляция Пирсона предполагает, что две рассматриваемые переменные измерены, по крайней мере, в интервальной шкале.

Корреляционные или статистические связи – связи, при которых численному значению одной переменной соответствует много значений другой переменной.

Корреляционные плеяды – сложная сеть корреляционных связей между многими признаками.

Коэффициент вариации – применяется при сравнении вариации различных признаков, представляет собой отношение σ к x, выраженное в процентах.

Коэффициент детерминации - это квадрат корреляции Пирсона между двумя переменными. Он выражает количество дисперсии, общей между двумя переменными.

Коэффициент корреляции r – указывает на степень связи в вариации двух переменных величин или на меру тесноты этой связи.

Коэффициент регрессии - количественная мера регрессии, вычисляемая если известны сигмы обоих вариационных рядов по признакам x и y, и коэффициенты корреляции между ними.

Кривая распределения (вариационная кривая) – графическое изображение вариационного ряда.

Критерий соответствия хи-квадрат χ² – показатель, определяющий степень соответствия фактических данных теоретически ожидаемым, или согласие фактических данных с предложенной гипотезой.

Критерий Стьюдента t – применяется при малых выборках (n ≤ 30), характеризует отклонение выборочных средних от генеральной средней. Устанавливает тот факт, что среднее квадратическое отклонение для малых выборок постоянно отличается от того, которое ожидалось бы при нормальном распределении.

Круговая диаграмма - последовательность значений переменной изображается в виде последовательных круговых секторов (термин "круговая диаграмма" был впервые использован Хаскеллом в 1922 г.); размер каждого сектора пропорционален соответствующему значению. Значения должны быть больше 0 (нулевое и отрицательные значения не могут быть представлены в виде круговых секторов). Круговая диаграмма интерпретирует данные самым непосредственным образом: одно наблюдение соответствует одному сектору.

Лимиты (пределы) – значения крайних классов, верхняя и нижняя граница вариационного ряда.

Метод регрессии – метод, позволяющий установить, как количественно меняется одна величина при изменении другой на единицу.

Медиана – значение варианты, находящееся точно в середине ряда.

Множественная корреляция – зависимость изменения величины x от одновременного изменения величин y,z и т.д.

Мода – значение модального класса, являющееся как бы типичной для всей совокупности.

Модальный класс – класс, обладающий наибольшей частотой.

Номинальные переменные - переменные, которые могут принимать конечное множество значений, например, Пол = { Муж, Жен }.

Нормальная вариационная кривая – симметричная плавная кривая, при которой верхние границы ломанной линии полигона сливаются в гладкую кривую линию.

Нормированное отклонение t – представляет собой отклонение тех или других вариант от их средней арифметической, выраженное в долях среднего квадратического отклонения.

Нулевая гипотеза - согласно этой гипотезе, первоначально принимается, что между данными показателями (или группами, на основе которых они получены) достоверного различия нет, т.е. что обе группы вместе составляют один и тот же однородный материал, одну совокупность.

Общность - это доля дисперсии, которая является общей для данной и всех остальных переменных. Доля дисперсии, которая является характерной для данной переменной (иногда называется характерностью) получается после вычитанием общности из дисперсии переменной. Другими словами дисперсия переменной есть общность плюс характерность. Обычно вначале в качестве оценки общности используют коэффициент множественной корреляции выбранной переменной со всеми другими.

Объем совокупности – число единиц совокупности.

Отрицательная корреляция - обратная зависимость между признаками: увеличение одного признака соответственно связано с уменьшением другого.

Ошибка выборочности или ошибка репрезентативности - представляют собой среднюю величину расхождения между средними значениями изучаемых признаков в выборках и генеральной совокупности.

Ошибка выборочности коэффициента корреляции – мера расхождения между коэффициентами корреляции для выборочной и генеральной совокупности.

Полигон распределения – графическое изображение конкретных вариационных рядов, применяющееся при дискретной вариации.

Положительная корреляция – прямая зависимость между признаками: при увеличении одного увеличивается и другой.

Поправка на непрерывность Иейтса – применяется при вычислении χ² в случае если исследуются малочисленные группы.

Ранжировка – расположение всех вариант по порядку от минимальных до максимальных значений.

Распределение Пуассона или пуасоново распределение – в биологии применяется для анализа редко наблюдаемые явления.

Симметричное распределение - если вы разобьете распределение пополам в точке среднего (или медианы), то распределения значений с двух сторон от этой центральной точки будут "зеркальным отображением" друг друга.

Случайная переменная – величина, изменяющаяся под влиянием многих случайных причин, которая может принимать разные значения.

Совокупность - всякое множество отдельных отличающихся друг от друга и в то же время сходных в некоторых существенных отношениях объектов.

Среднее - показывает "центральное положение" (центр) переменной и рассматривается совместно с доверительным интервалом. Обычно интерес представляют показатели (например, среднее), дающие информацию о популяции в целом. Чем больше размер выборки, тем более надежна оценка среднего. Чем больше изменчивость данных (больше разброс), тем оценка менее надежна.

Средняя арифметическая 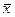– некоторая уравненная величина, отражающая основные свойсива всех членов совокупности.

Средняя геометрическая – статистический показатель, применяемый в случае, если возрастание данного признака происходит умножением пропорционально степени.

Стандартная ошибка - термин стандартная ошибка среднего был впервые введен Юлом (Yule, 1897). Эта величина характеризует стандартное отклонение выборочного среднего, рассчитанное по выборке размера n из генеральной совокупности, и зависит от дисперсии генеральной совокупности (сигма) и объема выборки (n).

Стандартное отклонение - (термин был впервые введен Пирсоном, 1894), это широко используемая мера разброса или вариабельности (изменчивости) данных.

Таблицы сопряженности – таблицы, в которых предусматривается распределение групп по признакам, сопряженность или связь между которыми нужно будет установить.

Теоретические (априорные) вероятности – вероятности, которые знают заранее до проведения опыта.

Уровень значимости – обозначает вероятность получения случайного отклонения от установленных с определенной вероятностью результатов. Вероятности 0,95 (95%) соответствует уровень значимости 0,05% (5%). При вероятности 0,99% (99%) уровень значимости 0,01 (1%).

Функциональная зависимость – зависимость, при которой, каждому значению одной переменной величины соответствует одно вполне определенное значение другой переменной.

Частная корреляция - корреляция между двумя переменными, вычисленная после устранения влияния всех других переменных, называется частной корреляцией

Число степеней свободы df – величина n-1.

Экстраполяция - прогнозирование неизвестных значений путем продолжения функций за границы области известных значений.

Эмпирические (апостериорные) вероятности – вероятности, которые получены после проведения опыта.

Date: 2015-09-18; view: 1343; Нарушение авторских прав