Дифференциальное уравнение теплопроводности

Изучение любого физического процесса сводится к установлению зависимости между величинами, характеризующими это явление. Для сложных физических процессов, в которых определяющие величины могут существенно изменяться в пространствен и времени, установить зависимость между этими величинами очень трудно. В этих случаях на помощь приходит метод математической физики. Метод исходит из того, что ограничивается промежуток времени и из всего пространства рассматривается лишь элементарный объем. Это позволяет в пределах элементарного объема и выбранного малого отрезка времени пренебречь изменением некоторых величин, характеризующих процесс и существенно упросить зависимость.

Выбранны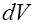й и 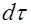в которых рассматривается изучаемый процесс с математической точки зрения являются величинами бесконечно малыми, а с физической - величинами еще достаточно большими, чтобы в их пределах прогнозировать строение среды и рассматривать ее как сплошную. Полученная таким образом зависимость является общим дифференциальным уравнением процесса. Интерпретируя его, можно получить аналитическую зависимость между величинами для всей области интегрирования и всего рассматриваемого промежутка времени.

Сделаем допущения:

· Тело однородно и изотропно

· Физические параметры постоянны

· Деформация рассматриваемого объема, связанная с изменением температуры, очень мала по сравнению с самим объемом.

В основе вывода положен закон сохранения энергии. Количество теплоты 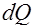введенное в элементарный объем 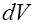извне за время 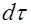вследствие теплопроводности, а также от внутренних источников, равно изменению внутренней энергии вещества, содержащегося в элементарном объеме.

*

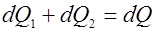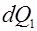- количество теплоты введенное в элементарный объем путем теплопроводности за время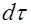

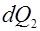- количество теплоты, которая за время 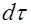отделилась в элементарном объеме 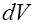за счет внутренних источников.

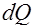- изменение внутренней энергии вещества в объеме 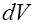за время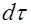

Выделим элементарный объем.

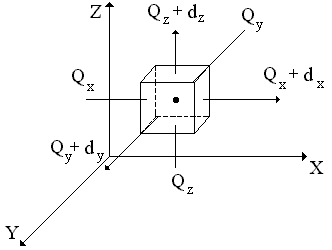
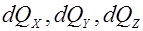- количество теплоты, подводимое к граням элементарного объема за 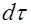в направление осей OX, OY, OZ.

- количество теплоты, подводимое через противоположные грани в тех же направлениях.

Количество теплоты, отведенное через противоположную грань элементарного параллелепипеда в направлении оси OX запишется

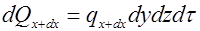
Разница между количеством теплоты, подведенного к элементарному параллелепипеду, и количеством теплоты, отведенного от него за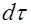

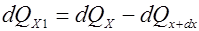
или

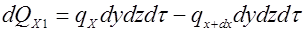
Функция 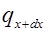является непрерывной в рассматриваемом интервале и может быть разложена в ряд Тейлора.

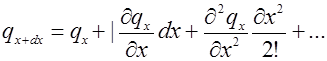
Взяв два первых члена ряда:

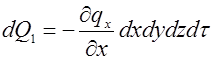
Аналогично для других осей:

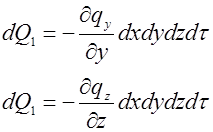
Количество теплоты 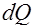, подведенное в результате теплопроводности к рассматриваемому объекту будет равно:

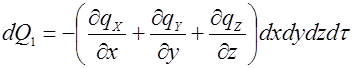
Для второй составляющей 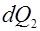. Количество теплоты, выделенное внутренними источниками в единицу объема среды в единицу времени через 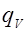тогда:

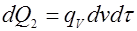
Третья составляющая в уравнении (*) найдется в зависимости от характера термодинамического процесса изменения системы. Вся теплота подведенная к элементарному объему, уйдет на изменение внутренней энергии вещества, заключенного в этом объеме.

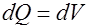
Для внутренней энергии объема.

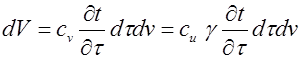
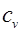- теплоемкость единицы объема

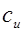- теплоемкость единицы массы

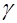- плотность вещества

Подставляя полученное выражение в (*) получим:

**

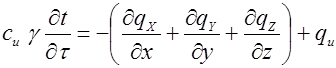или

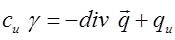
Учитывая то, что проекции вектора плотности теплового потока на координатные оси OX, OY, OZ:

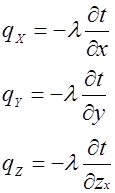
Подставляя это в (**), получим:

или

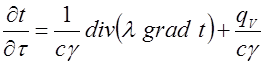
Это дифференциальное уравнение теплопроводности. Если теплофизические характеристики постоянны:

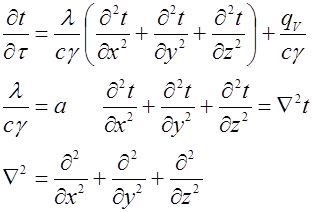
Из уравнения видно, что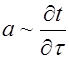

1. 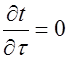- стационарный тепловой режим

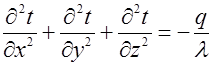- уравнение Пуассона

2. 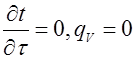- нет внутренних источников тепла.

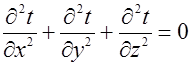- уравнение Лапласа.

Так как дифференциальное уравнение теплопроводности выводится на основе общих законов физики, то оно описывает явления теплопроводности в самом общем виде. Для выделения конкретного вопроса и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математическое описание всех частных особенностей рассматриваемого процесса. Эти частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности называется условиями однозначности или краевыми условиями.

Условия однозначности включают в себя:

· геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс.

· физические условия, характеризующие физические свойства среды и тела

· взаимные (начальные) условия, характеризующие распределение температур в изучаемом теле в начальный момент времени

· граничные условия, характеризующие взаимодействия рассматриваемого тела с окружающей средой.

Граничными условиями задается форма и линейные размеры тела, в котором протекает процесс

Физическими условиями задаются физические параметры тела, и может быть задан закон распределения внутренних источников тепла.

Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени.

Граничные условия могут быть заданы несколькими способами

Граничные условия первого рода задается распределение температуры на поверхности тела для каждого момента времени

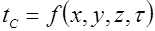
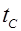- температура поверхности тела

Граничные условия второго рода з адаются значения теплового набора для каждой точки поверхности и любого момента времени

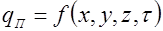
- плотность теплового потока на поверхности тела

Граничные условия третьего рода задается температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой. Граничные условия третьего рода характеризуют закон теплообмена между поверхностью и окружающей средой в процессе охлаждения и нагрева.

Закон Ньютона - Рихмана

Количество теплоты, отдаваемое единицей поверхности тела в единицу времени пропорционально разности температур поверхности тела и окружающей среды.

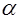- коэффициент пропорциональности (коэффициент теплообмена)

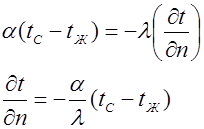
Иногда ни одно из перечисленных граничных условий задать невозможно. Тогда для определения теплового взаимодействия между телами приходится решать сопряженную задачу. При решении таких задач должны выполняться условия равенства температур и тепловых потоков по обе стороны отграницы раздела. В общем случае условия сопряженности можно записать:

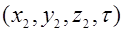- источники теплоты на поверхности границы

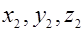- координаты поверхности раздела сред

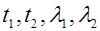- температуры и коэффициенты теплопроводности сред.

При отсутствии на границе раздела сред процессов с выделением или поглощением теплоты, условия сопряженности принимают вид:

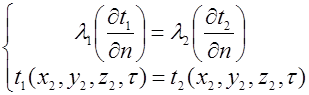
Решение сопряженной задачи связано с нахождением температурных полей по обе стороны границы раздела.

Date: 2015-09-18; view: 701; Нарушение авторских прав