Переход через критическую скорость (сопло Лаваля)

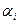- угол раскрытия канала.

Начальные параметры: , , .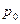

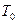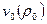Параметры среды: , , .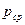

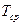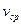Можно поставить две задачи:

1. Найти линейную скорость, массовую скорость и массовый расход, при известной геометрии аппарата.

2. Найти геометрию аппарата, при известном массовом расходе.

Решаем вторую задачу.

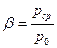
Сравнивая величину с 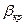, получим три варианта:

1. Докритический режим, .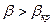

2. Критический режим: .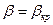

3. 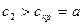Закритический режим: .

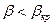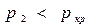Для обеспечения закритического режима истечения, характеризующегося условием (), необходимо дополнить суживающееся сопло расширяющейся частью, в выходном сечении которой возможно достичь значения давления ниже критического. Такое комбинированное сопло называется соплом Лаваля.

Нужно найти площади сечений: , , .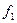

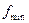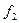Уравнение неразрывности: 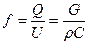. Подставляя в это уравнение массовые скорости, можно найти площади сечений, но для каждого случая нужно знать величину , то есть нужно с помощью уравнений процессов (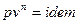 и 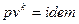) найти давления 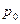, , 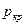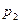. Зная площади сечений можно найти характеристические размеры сечений.

Длины можно найти геометрически: 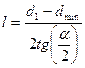, где .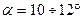

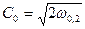
Для адиабатного процесса 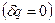потенциальная работа находится по формуле: 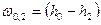, тогда линейная скорость .

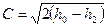Общие закономерности процесса истечения.

Цель: установление связи между f,c,p.

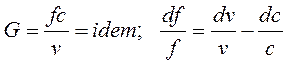1.уравнение неразрывности

2.уравнение распределение потенциальной работы

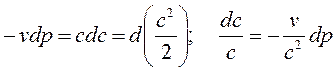
3.показатель процесса

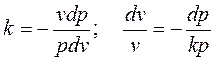Отсюда первое и второе дифференциальное уравнение

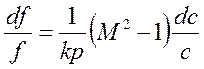
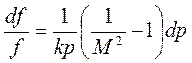
Date: 2015-09-18; view: 871; Нарушение авторских прав