
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача об оптимальном использовании сырья при производстве изделий
|
|
Планирование рациональных покупок продуктов питания
Задача о диете. Очень часто эта задача линейного программирования называется как задача о смесях – задача подбора оптимального состава смеси, отвечающей заданным условиям. Это может быть и состав сплава, отвечающий заданным характеристикам, и набор праздничных подарков и др.
Содержание задачи
Нередко возникают задачи, связанные с осуществлением рациональных покупок продовольственных товаров, обеспечивающих необходимый рацион питания (например, семьи при ограниченном ассортименте продуктов).
Такого типа задачи решаются в условиях ограничений по ассортименту товаров, товарных запасов, стоимости, суточных норм потребления питательных веществ и их содержания в продуктах и др.
Целью оптимизации является выбор из всех возможных вариантов такого набора продуктов, который бы содержал необходимое количество питательных веществ и имел минимальную стоимостью.
Допустим, что мы имеем набор продуктов: мясо, рыба, молоко, масло, сыр, крупа, картофель стоимость килограмма которых составляет
С1, С2,…,СJ,…, Cn, соответственно.
Запасы продуктов ограничены:
А1, А2,…, Аj,…, Аn,
Содержание питательных веществ – белков, жиров, углеводов, минеральных солей… - в одном килограмме каждого продукта известно и составляет соответственно:
Q11, Q21,…,Qi1,…,Qn1
Кроме того, известны нормы суточной потребности человека в каждом питательном веществе:
B1, B2,…,Bi,…,Bm
Перечисленные показатели могут быть записаны в виде системы линейных ограничений:
Q11*X1+ Q12*X2+…+ Q1j*Xj +…+ Q1n*Xn ≥B1
Q21*X1+ Q22*X2+…+ Q2j*Xj +…+ Q2n*Xn ≥B2
………………………………………………………
Qm1*X1+ Qm2*X2+…+ Qmj*Xj +…+ Qim*Xn ≥Bm
Еще одно ограничение связано с тем, что количество каждого продукта в рационе, с одной стороны, не может быть величиной отрицательной, с другой – количество закупленных продуктов ограничена его запасами:
0 £ Х1 £ А1, 0 £ Х2 £ А2,…, 0 £ Хj £ Аj
F Необходимо определить такое количество закупаемых продуктов
Х1, Х2,…, Хj,…, Хn, которое бы обеспечило потребность человека в питательных веществах при минимальной стоимости набора продуктов и описывалось бы линейной формой связи целевой функции:
F = {C1*X1+ C2*X2+…+ Cj*Xj+…+ Cn*Xn}ðmin.
В более компактном виде экономико-математическая формулировка и модель имеют вид:
найти оптимальное количество продуктов питания
Х10, Х20,…, Хj0,…, Хn0
cистемы линейных ограничений
∑ Qij*Xj ≥ Bi i Î m,
0 £ Xj ≥ Aj J Î n,
которые обращают в минимум линейную форму связи целевой функции:
F = Cj*Xj ðmin,
что позволяет получить экономный рацион суточного потребления продуктов, т.е. оптимальное решение задачи.
Пример
Для поддержания нормальной жизнедеятельности человеку необходимо ежедневно потреблять 118 г. белков, 56 г жиров, 500 г углеводов, 8 г минеральных солей.
Количество питательных веществ, содержащихся в одном килограмме имеющихся в магазине продуктов питания, а также их стоимость приведены в таблице.
Необходимо составить дневной рацион, содержащий не менее суточной нормы потребности человека в необходимых питательных веществах и обеспечивающий минимальную общую стоимость продуктов.
FВ соответствии с вышеизложенным, экономико – математическая формулировка и модель будут иметь вид:
найти оптимальное количество закупаемых продуктов питания
Х10, Х20,…, Хj0,…, Хn0
системы линейных ограничений, связанных с суточной нормой потребления:
180*Х1+190* Х2+30* Х3+70* Х4+260* Х5+130* Х6+21* Х7 ≥118
20*Х1+3* Х2+40* Х3+805* Х4+310* Х5+30* Х6+2* Х7 ≥56
0*Х1+0* Х2+50* Х3+6* Х4+20* Х5+650* Х6+200* Х7 ≥500
9*Х1+10* Х2+7* Х3+12* Х4+60* Х5+20* Х6+70* Х7 ≥8
Х1>0, Х2>0, Х3>0, Х4>0, Х5>0, Х6>0, Х7>0,
которые обращают в минимум затраты на покупку продуктов питания
F = {70*Х1+ 40*Х2+ 10*Х3+ 55*Х4+75*Х5+15*Х6+10*Х7}ðmin
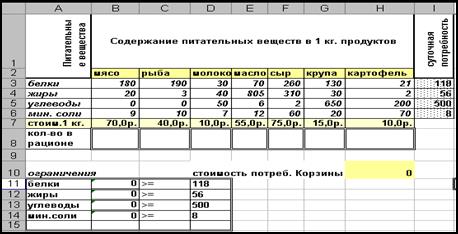
Рис. 14. Таблица для решения задачи о планировании рациональных покупок
На листе Excel:
В ячейке H10 записана целевая функция (F) =СУММПРОИЗВ(B7:H7;B8:H8)
В ячейках В11:В14 записаны формулы ограничений
=СУММПРОИЗВ(B3:H3;$B$8:$H$8)
=СУММПРОИЗВ(B4:H4;$B$8:$H$8)
=СУММПРОИЗВ(B5:H5;$B$8:$H$8)
=СУММПРОИЗВ(B6:H6;$B$8:$H$8)
После того как на листе Excel размещены формулы целевой функции и функций ограничений выполните команду СЕРВИСðПОИСК РЕШЕНИЯ и в открывшемся 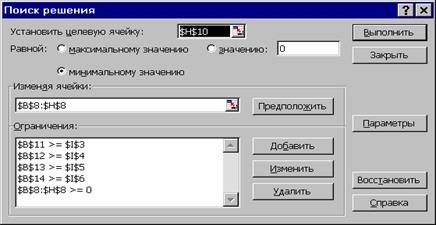 диалоговом окне выполните все необходимые установки.
диалоговом окне выполните все необходимые установки.
Рис. 15 Диалоговое окно «Поиск решения» с введенными адресами изменяемых ячеек, целевой функции и функций ограничений
После щелчка на кнопке «Выполнить» в строке «Количество в рационе» появятся значения рекомендуемых наборов продуктов. В данной постановке задачи. оптимальный набор продуктов, удовлетворяющий поставленным условиям состоит из 36 масла и 888 г крупы. При его стоимости 15.32 руб.
Задача об оптимальном использовании сырья при производстве изделий
Определим оптимальный план выпуска продукции в условиях дефицита сырья.
Предположим, что предприятие намерено выпускать два вида продукции, используя для этого три вида сырья. При этом, цена единицы первоговида продукции равна 25000 руб., а второго - 50000 руб.
Известны нормы расхода сырья при производстве единицы продукции (см. Таблицу)
| продукция | Запасы сырья | |
| вид1 | вид2 | |
| 1,2 | 1,9 | |
| 2,3 | 1,8 | 56,6 |
| 0,1 | 0,7 |
Обозначим количество произведенной продукции вида 1 через С1, а вида 2 через С2. Тогда целевая функция, которая должна обеспечить получение максимального величины прибыли, должна иметь вид:
У = 25000*С1+ 50000*С2
Date: 2015-09-18; view: 6856; Нарушение авторских прав