Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Решение задачи. Для построения оптимального плана выпуска продукции, на листе Excel создадим таблицу, подобную показанной на рисунке
|
|
Для построения оптимального плана выпуска продукции, на листе Excel создадим таблицу, подобную показанной на рисунке.
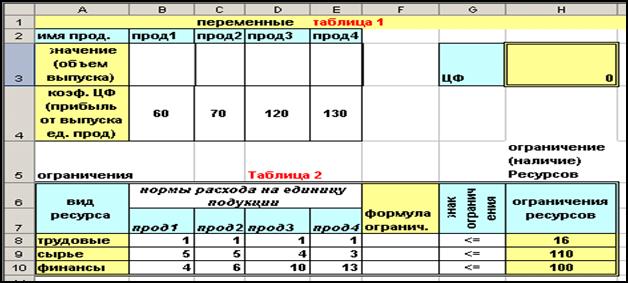
F В соответствии с тем как было рассмотрено выше, запишем в соответствующих ячейках таблицы формулы для вычисления целевой функции и функций ограничений (построим модель решения задачи).
Целевую функцию размещаем в ячейке Н3, в которую программируем формулу:
=B4*B3+C4*C3+D4*D3+E4*E3.
Ограничения:
Левые части неравенств ограничений задаем формулами в ячейках:
F8 ( трудовые ресурсы) формула:
=B8*B3+C8*C3+D8*D3+E8*E3,
F9 ( сырьё) формула:
=B9*B3+C9*C3+D9*D3+E9*E3,
F10 ( финансы) формула:
=B10*B3+C10*C3+D10*D3+E10*E3.
Лимиты на ресурсы помещаем в ячейки H8, H9 и H10.
FПосле того как в соответствующие ячейки таблицы записаны формулы целевой функции и функций ограничений, выполним команду СЕРВИСðПОИСК РЕШЕНИЯ и в открывшемся диалоговом окне выполним необходимые установки:
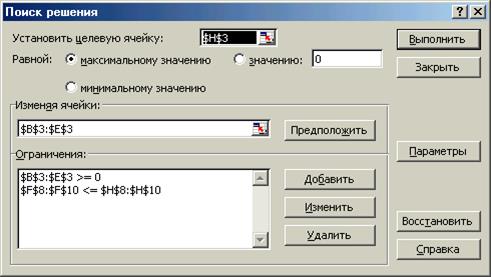
· · В поле «Установить целевую ячейку» введем адрес ячейки, содержимое которой должно быть оптимизировано. В нашем случае это ячейка «$Н$3», содержащая формулу вычисления дохода предприятия
· · В группе опций «Равной» установим необходимое значение целевой функции (ячейки $Н$3). В нашем примере выбираем опцию - «Максимальному значению»
· · В поле «Изменяя область ячеек» необходимо задать адреса ячеек, которые могут изменяться в процессе оптимизации решения. В нашем случае, это ячейки, содержащие информацию о плановом количестве выпуска товаров - ячейки $B$3: $Е$3. ( При нажатии кнопки «Предположить» Excel выделяет область ячеек, на которые прямо или косвенно ссылается целевая ячейка )
F Для того, чтобы ввести в диалоговое окно ограничения:
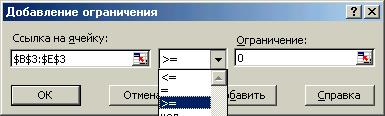
· · установите курсор мыши в поле «Ограничения»;
· · щелкните на кнопке «Добавить», после чего на экране появится диалоговое окно, в которое необходимо ввести все установки ограничений;
· · В поле «Ссылка на ячейку» необходимо ввести адрес ячейки, содержащее формулу ограничения;
· · в окно «Ограничение» вводится адрес ячейки, содержащей значение ограничения (либо численное значение ограничения)
· · содержимое полей «Ссылка на ячейку» и «Ограничение» соединяется с помощью операторов сравнения, выбираемых из раскрывающегося списка
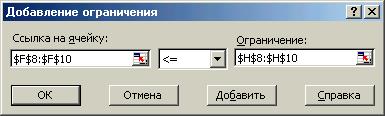
В нашей задаче формулы ограничений на количество используемых ресурсов были записаны в ячейках F8:F10, а сами значения ограничений в ячейках Н8:Н10
· · Введем первое ограничение, указав в поле «Ссылка на ячейку» адрес ячейки, содержащей формулу ограничений по трудовым ресурсам (F6) (Обратите внимание на то, что после того как в поле “Ссылка на ячейку» Вы указали адрес ячейки, содержащей формулу ограничений, Excel автоматически преобразует эту ссылку в абсолютную.)
· · в поле «Ограничение» введем адрес ячейки, содержащей значение ограничения по трудовым ресурсам (Н8) (либо само числовое значение ограничения)
· · выберем оператор сравнения £ (количество использованных трудовых ресурсов должно быть меньше (или равно) имеющихся в наличии)
FДля ввода нового ограничения, щелкните на кнопке «Добавить».
· · Повторив описанные выше действия, введите ограничения по сырью и финансам;
· · щелкните на кнопке «Добавить» и введите ограничения для области решения задачи. В нашем случае, таким ограничением будет то, что количество выпускаемой продукции не может быть величиной отрицательной. Т.е., необходимо ввести ограничения В3 ³ 0; C3 ³ 0; D3 ³ 0; E3 ³ 0.
· · Завершив ввод ограничений, щелкните на кнопке «ОК»
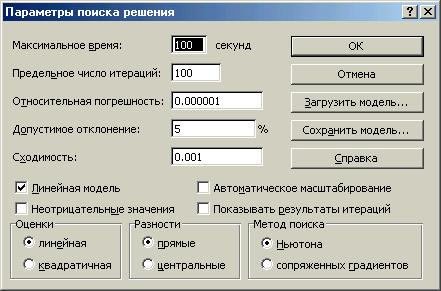FВо вновь открывшемся диалоговом окне «Поиск решения»:
· · Щелкните на кнопке «Параметры» и сделайте необходимые установки (пояснения к этому окну см. в приведенной ниже таблице) и щелкните на кнопке «ОК»
· · В диалоговом окне «Поиск решения», щелкните на кнопке «Выполнить».
FВ результате выполненных действий Excel выведет на экран сообщение
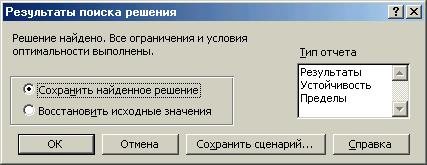
Рис.2 Сообщение Excel о результатах поиска решения
· щелкните на кнопке «ОК» ( о создании отчетов и их анализе будет рассказано ниже в разделе «Анализ оптимального решения») и результаты оптимального решения задачи будут внесены в созданную таблицу
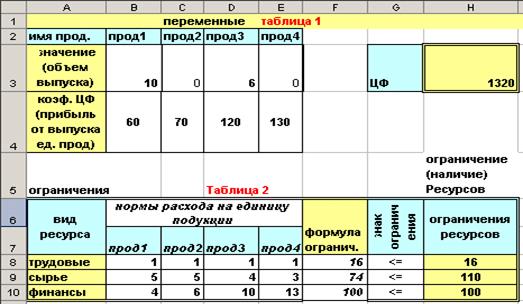
Рис. 3 Фрагмент таблицы Excel с результатами решения задачи по разработке оптимального плана выпуска продуктов.
Как видно из приведенного на рисунке решения максимальная прибыль = 1320 руб. будет получена при выпуске двух видов продуктов: Прод1 и Прод3 в количествах 10 и 6, соответственно. При этом, все ограничения, поставленные нами при решении задачи - выполнены
Примечание:
1. При создании формул целевой функции и функций ограничений оказывается очень удобным использование функции Excel СУММПРОИЗВ(), позволяющую находить сумму произведений нескольких векторов. Так например вместо записи целевой функции в виде = B4*B3+C4*C3+D4*D3+E4*E3
можно было записать =СУММПРОИЗВ(B3:E3;B4:E4)
2. При вводе ограничений мы вводили каждое из них отдельно. В большинстве случаев оказывается возможным ввод ограничения виде массива. Так, например, вместо раздельного ввода ограничений по каждому виду ресурса, можно ввести ограничение в виде массива $F$8:$F$10 £ $H$8:$H$10
Назначение основных элементов диалогового окна
«Параметры поиска решения»
| Максимальное время | Служит для ограничения времени, отпускаемого на поиск решения задачи. В поле можно ввести время (в секундах) не превышающее 32767; значение 100, используемое по умолчанию, подходит для решения большинства простых задач |
| Число итераций | Служит для управления временем решения задачи, путем ограничения числа промежуточных вычислений. В поле можно ввести время (в секундах) не превышающее 32767; значение 100, используемое по умолчанию, подходит для решения большинства простых задач. |
| Точность | Служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать десятичную дробь от 0 (нуля) до 1. Чем больше десятичных знаков в задаваемом числе, тем выше точность — например, число 0,0001 представлено с более высокой точностью, чем 0,01 |
| Допустимое отклонение | Служит для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. При указании большего допуска поиск решения заканчивается быстрее |
| Сходимость | Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Сходимость применяется только к нелинейным задачам, условием служит дробь из интервала от 0 (нуля) до 1. Лучшую сходимость характеризует большее количество десятичных знаков — например, 0,0001 соответствует меньшему относительному изменению по сравнению с 0,01. Лучшая сходимость требует больше времени на поиск оптимального решения |
| Линейная модель | Служит для ускорения поиска решения линейной задачи оптимизации |
| Показывать результаты итераций | Служит для приостановки поиска решения для просмотра результатов отдельных итераций. |
| Автоматическое масштабирование | Служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине — например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей. |
| Значения не отрицательны | Позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение |
| Оценка | Служит для указания метода экстраполяции — линейная или квадратичная — используемого для получения исходных оценок значений переменных в каждом одномерном поиске. Линейная. Служит для использования линейной экстраполяции вдоль касательного вектора. Квадратичная. Служит для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач. |
| Производные | Служит для указания метода численного дифференцирования — прямые или центральные производные — который используется для вычисления частных производных целевых и ограничивающих функций. Прямые. Используется в большинстве задач, где скорость изменения ограничений относительно невысока. Центральные. Используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдается сообщение о том, что получить более точное решение не удается. |
| Метод | Служит для выбора алгоритма оптимизации — метод Ньютона или сопряженных градиентов — для указания направление поиска. Метод Ньютона. Реализация квазиньютоновского метода, в котором запрашивается больше памяти, но выполняется меньше итераций, чем в методе сопряженных градиентов. Метод сопряженных градиентов. Реализация метода сопряженных градиентов, в котором запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях. |
| Загрузить модель | Служит для отображения на экране диалогового окна Загрузить модель, в котором можно задать ссылку на область ячеек, содержащих загружаемую модель |
| Сохранить модель | Служит для отображения на экране диалогового окна Сохранить модель, в котором можно задать ссылку на область ячеек, предназначенную для хранения модели оптимизации. Данный вариант предусмотрен для хранения на листе более одной модели оптимизации — первая модель сохраняется автоматически |
Date: 2015-09-18; view: 433; Нарушение авторских прав