
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лабораторный практикум №1
|
|
Решение задач оптимизации
Задачи оптимизации - это задачи, в которых требуется выбрать лучший вариант решения из нескольких возможных.
Теория оптимизации формализует совокупность действий, связанных с достижением определенных целей, например: определение ассортимента продукции, составление эффективного графика работы сотрудников, разработка схемы перевозок. Операция характеризуется количественными факторами двух видов: неконтролируемыми (значение известны, но не зависят от воли принимающего решение) и контролируемыми (управляемыми, значения зависят от лица, принимающего решения, но в определенных приделах, выражаемых математическими ограничениями).
Решение – это любой допустимый (удовлетворяющий ограничениям) набор значений факторов. Критерий качества решения, выраженный с помощью функции, называют критерием оптимальности, а функцию позволяющую оценить качество решения, - целевой функцией.
Оптимальное решение – решение, на котором достигается экстремум целевой функции. Если ограничения задаются системой линейных неравенств и целевая функция является линейной, то задача называется задачей линейного программирования.
Отличие экономико-математической постановки задачи оптимизации в табличном процессоре от традиционной экономико-математической постановки состоит в том, что в формулах задаются не символьные обозначения переменных и параметров, а координаты ячеек таблицы, в которых хранятся эти переменные.
Задачей данной работы является определение, на основании данных представленных в таблице №1, оптимального объема реализации товаров (№1-№4) организации ООО «Х» с целью получения максимальной прибыли, при этом также следует учесть:
- месячное ограничение по финансированию закупки товара – 19 500 тыс. руб.;
- месячное ограничение по количеству рейсов автотранспорта – 26.
Таблица №1
Ассортимент товаров ООО «Х» в 2010 году.
| Список товаров | ||||
| Предполагаемый объем реализации в месяц (шт.) | ||||
| Предполагаемый максимальный объем реализации в месяц (шт.) | ||||
| Вместимость склада (шт.) | ||||
| Вместимость машины (шт.) | ||||
| Цена реализации 1 ед. (тыс. руб.) | 18,47 | 18,24 | 18,39 | 18,53 |
| Цена приобретения 1 ед. (тыс. руб.) | 15,72 | 15,53 | 16,43 | 17,31 |
Алгоритм выполнения:
A. Для нахождения решения оптимизационной задачи – определения оптимального объема реализации товаров с целью получения максимальной прибыли применим надстройку Поиск решения. Надстройка - вспомогательная программа, служащая для добавления в Microsoft Office специальных команд или возможностей. Надстройка Поиск решения находится в группе Сервис.
b. В модели оптимизации участвуют три элемента: целевая ячейка, изменяемые ячейки и ограничения.
Целевая ячейка представляет задание или цель. Цель задачи получить максимальную прибыль, исходя из имеющихся возможностей. Таким образом, целевой ячейкой будет являться прибыль по всем товарам №1-№4. Для ее определения необходимо создать электронную таблицу 1.1 на основе данных представленных в таблице №1 и ниже добавить одну строку «Прибыль на 1 ед. (тыс.руб.)» = Цена реализации 1 ед. (тыс.руб.) – Цена приобретения 1 ед. (тыс.руб.) (рис.3).

Рис. 3.
Для расчета общей прибыли и ограничений по всем товарам необходимо создать электронную таблицу 1.2 (см. рис. 4 и рис. 5), где в столбце «Ограничение» данные (26 и 19 500) взяты из условия задачи. Ограничение по общей прибыли не заполняется.
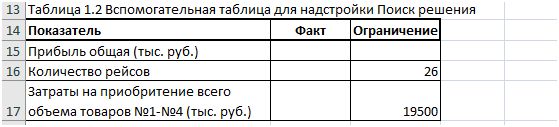
Рис. 4.
Для расчета общей прибыли в столбце «Факт» электронной таблицы 1.2 (рис.4) воспользуйтесь формулой СУММПРОИЗВ, она перемножает соответствующие значения в диапазонах ячеек и возвращает сумму этих значений. Прибыль общая вычисляется следующим образом: =СУММПРОИЗВ ( диапазон ячеек по показателю «предполагаемый объем реализации» из таблицы 1.1; диапазон ячеек по показателю «прибыль на 1 ед.» из таблица 1.1 ). Для указанного ниже примера (рис. 5) формула в ячейке В11 («прибыль общая факт») будет выглядеть так: =СУММПРОИЗВ(B2:E2;B8:E8).

Рис. 5. Демонстрация решения указанного практикума
Для расчета количества рейсов в столбце «Факт» необходимо разделить показатель «предполагаемый объем реализации» из таблицы 1.1. на показатель «вместимость машины» и суммировать их по каждому товару №1-№4. Например, в ячейке В12 («кол-во рейсов», рис.5) можно написать:=B2/B5+C2/C5+D2/D5+E2/E5.
Для расчета третьего показателя – общих затрат на приобретение товаров №1-№4 можно воспользоваться указанной выше формулой: =СУММПРОИЗВ (диапазон ячеек по показателю «предполагаемый объем реализации» из таблицы 1.1; диапазон ячеек по показателю «цена приобретения 1 ед.» из таблицы 1.1). Для примера, указанного на рис. 5, формула в ячейке В13 будет выглядеть так: =СУММПРОИЗВ(B2:E2;B7:E7).
Выполнив вышеуказанные действия столбец «Факт» будет полностью заполнен.
c. Откройте диалоговое окно Поиск решения (рис. 5).
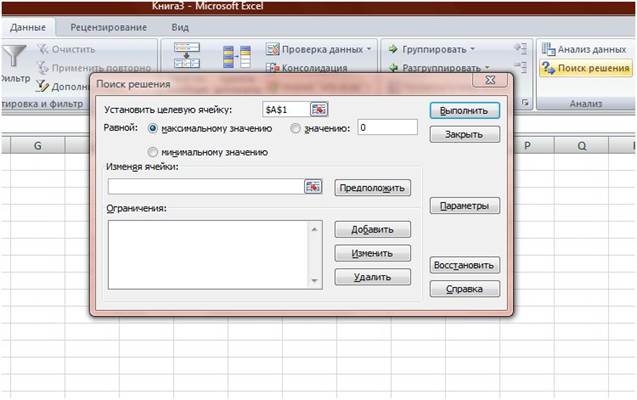
Рис. 5.
Целевая ячейка – цель максимизировать прибыль, таким образом, ей соответствует показатель «прибыль общая» из таблицы 1.2. Для указания целевой ячейки щелкните в поле Установить целевую ячейку и затем выберите ячейку с общей прибылью из таблицы 1.2 (ячейка В11).
Изменяемые ячейки – диапазон ячеек показателя «предполагаемый объем реализации» (диапазон B2:E2). Изменяемые ячейки должны быть прямо или косвенно связаны с целевой ячейкой. Допускается установка до 200 изменяемых ячеек.
Исходя из условий задачи, определены следующие четыре ограничения, которые необходимо внести в диалоговое окно Добавление ограничений нажав кнопку Добавить (рис. 6):
- количество рейсов «факт» <= количество рейсов «ограничение»;
- общие затраты «факт» <= общие затраты «ограничение;
- диапазон «предполагаемый объем реализации» <= диапазон «вместимость склада»;
- диапазон «предполагаемый объем реализации» <= диапазон «предполагаемый максимальный объем реализации». Указанное ограничение присутствует в связи с тем, что предполагаемый объем реализации является возможно максимальным на существующем рынке и не может превысить своего значения, в связи с этим в таблице 1.1 присутствуют две строки с одинаковыми показателями.
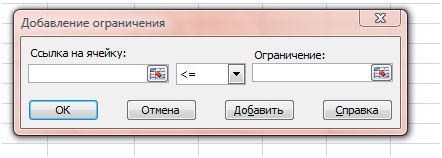
Рис. 6.
Так же необходимо ввести ограничение, которое определяет, что все изменяемые ячейки не должны принимать отрицательное значение. Оно задается в диалоговом окне Параметры поиска решения. Щелкните кнопку параметры в диалоговом окне Поиск решения и отметьте опции Линейная модель и Неотрицательные значения (рис. 7).
Модель поиска решения является линейной при соблюдении следующих условий:
- целевая ячейка вычисляется как сумма выражения вида (изменяемая ячейка)*(константа);
- каждое ограничение удовлетворяет требованию линейной модели – каждое ограничение вычисляется как сумма выражения вида (изменяемая ячейка)*(константа) и сравнивается с константой.
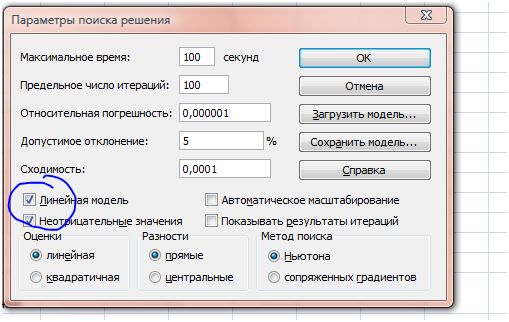
Рис. 7.
Если установлен параметр линейная, Поиск решения использует алгоритм симплекс-метода для поиска оптимального решения. Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Метод был разработан американским математиком Джорджем Данцигом в 1947 году.
Если же модель поиска решения линейная, но не установлен параметр линейная, применяется очень неэффективный алгоритм (метод GRG2) и поиск оптимального решения может быть затруднен.
Щелкнув OK в диалоговом окне Параметры поиска решения, активируется диалоговое окно Поиск решения, далее необходимо нажать кнопку Выполнить. Откроется диалоговое окно Результаты поиска решения (рис. 8).
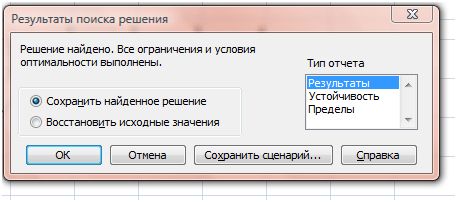
Рис. 8.
Кроме вставки оптимальных значений в изменяемые ячейки, Поиск решения позволяет представлять результаты в виде трех отчетов: Результаты, Устойчивость и Пределы. Для генерации одного или нескольких отчетов необходимо выделить их название в окне диалога Результаты поиска решения.
Выделите отчет Результаты и нажмите кнопку ОК. Отчет будет сформирован в новом листе.
Date: 2015-09-18; view: 411; Нарушение авторских прав