Теорема Эрроу

Систематическое исследование всех возможных систем голосования провел в 1951 г. Кеннет Эрроу из Стенфордского университета.Он поставил вопрос в наиболее общем виде: можно ли создать такую систему голосования, чтобы она была одновременно рациональной, демократической и решающей. Вместо попыток изобретения такой системы Эрроу предложил набор требований, аксиом, которым эта система должна удовлетворять.

Аксиома 1 - аксиома универсальности - требует, чтобы система голосования была действенной при любом возможном распределении голосов, при любых предпочтениях избирателей.

Аксиома 2 - аксиома единогласия, в соответствии с которой единогласное мнение всех голосующих за выбор определенного кандидата должно привести к коллективному выбору этого же кандидата.

Аксиома 3 - аксиома независимости от несвязанных альтернатив - говорит о том, что в групповом упорядочении порядок определенных кандидатов не должен измениться при изменении отношений избирателей к прочим кандидатам.

Аксиома 4 - аксиома полноты, согласно которой система голосования должна сравнивать любую пару кандидатов.

Аксиома 5 - условие транзитивности предполагает, что система голосования не должна нарушать транзитивность отношений избирателей, в ней не должно быть противоречий.

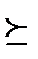
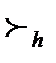
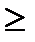
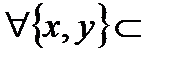
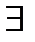Теорема Пусть в множестве альтернатив 3 элемента, и возможны все рациональные профили (R) или вообще все профили, в которых любые две альтернативы различимы (P),тогда всякая функция социального выбора F,которая оптимальна по Парето и удовлетворяет условию попарной независимости, является диктаторской,т.е. агент h такой,что O и любого профиля (…) x социально предпочтителен y тогда и только тогда, когда x y

Определение. Профиль предпочтений называется рациональным,

если он является линейным порядком, то есть любые два исхода сравнимы и выполняется условие транзитивности.

Оптимальность по Парето

Пусть пара исходов x,y 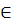O такова, что для каждого агента i исход x

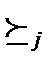
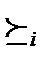не хуже, и при этом для какого-нибудь агента он строго лучше:для всех i x y, и существует такое j, что x y. Тогда функция социального выбора f называется эффективной по Парето, если для каждой такой пары исходов результат функции социального выбора

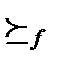
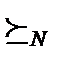
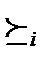f (,…,) ставит x перед y: x y.

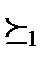
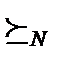
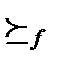
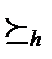Определение: функция социального выбора f называется диктаторской, если существует такой агент h, что для любых x,y 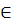O и любого профиля (,…,) x y тогда и только тогда, когда x y

Примечание: если в O два элемента, 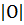=2, то теорема неверна. Например,функция социального выбора «большинство голосов» в данном случае и не диктаторская и правдиво реализуемая в доминантных стратегиях.

Определив пять аксиом - желательных свойств системы голосования, Эрроу доказал, что системы, удовлетворяющие этим аксиомам, обладают недопустимым с точки зрения демократических свобод недостатком: каждая из них является правилом диктатора.

Требование исключения диктатора приводит к невозможности создания системы голосования, удовлетворяющей всем аксиомам Эрроу.

Поэтому результат Эрроу называют теоремой невозможности.

Литература:

• Э.Мулен «Кооперативное принятие решений:Аксиомы и модели»,издательство «Мир» 1991г.

• Малыхин В.И., Моисеев С.И. «Математические методы принятия решений»,учебное пособие,2009 г.

• О.И.Ларичев «Теория и методы принятия решений…»,Москва, «Логос»,2002 г.

• http://gendocs.ru

• http: // logic.pdmi.ras.ru

Date: 2015-09-05; view: 787; Нарушение авторских прав