
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Ротор биологического временного поля растений и электромагнитная теория Максвелла
|
|
Предложена теория биологического временного поля, способная объединить или «работать» на различных уровнях иерархии организации процессов фотосинтеза, фотодыхания и дыхания поддержания. Исходя из теории, естественным образом осуществляется подразделение продукционного процесса растений на фотосинтез, фотодыхание и дыхание поддержания. Становится ясна роль фотодыхания – это процесс, обеспечивающий неразрывную связь движений биологического временного поля. Фактор биологического временного поля является объединяющим звеном на различных уровнях иерархии биологических процессов растения.
Ключевые слова: фотосинтез, дыхание, биологическое время, внешняя среда, ротор, продукционный процесс, рост, развитие.
Введение. Фотосинтез – единый на Земле, уникальный процесс в биосфере, благодаря которому при участии растений осуществляется запасание солнечной энергии и преобразование простых неорганических веществ на сложные органические образования. При фотосинтезе рассматривают преобразование электромагнитной энергии и, её запасание в различных видах. Общее уравнение этого процесса имеет вид:
6 СО 2 + 6Н 2 О → С 6 Н 12 О 6 + 6 О 2. (1)
При таком преобразовании углекислоты и воды в разнообразные органические вещества первым, необходимым условием такого преобразования является наличие света и хлорофилла [1]. Различают световую и темновую стадию фотосинтеза.
Исследования процесса фотосинтеза в настоящее время быстро развиваются. Однако первичные реакции процесса фотосинтеза и процесс переноса электронов до сих пор не выяснены. В плане этой проблемы существуют различные теории и гипотезы [2, 3]. Установлено, что существуют две фотосистемы: Фотосистема I и Фотосистема II. Этим фотосистемам присуща «антена», которая является первичным механизмом поглощения кванта света. В рамках установленных фактов существует теория Z -схемы электронного транспорта при фотосинтезе, рис. 1. Z -схема оказалась удобной для того, чтобы ввести понятие о двух последовательно работающих фотохимических реакциях и об электронах, движущихся «вниз» по энергетическим уровням от сильного восстановителя к сильному окислителю, которые образуются в каждой из фотосистем при поглощении света. Однако, в настоящее время еще мало точных сведений о движении электронов «вниз» по энергетическим уровням. Транспорт электронов между фотосистемами происходит по хорошо известной цепи переносчиков, тогда как на самом деле электроны от многих реакционных центров фотосистемы II могут накапливаться в некоторых пулах, подобно электронам, донированным одним реакционным центром при последовательном поглощении нескольких квантов света. Фотосинтетическая мембрана растения осуществляет замечательную реакцию: она превращает энергию поглощенных квантов света в окислительно-восстановительный потенциал. При этом происходит преобразование энергии из очень короткоживущей ее формы в форму достаточно долгоживущую. Первичные процессы фотосинтеза проходят в тилакоидных мембранах, которые имеют свое морфологическое строение и располагаются в хлоропластах.
Как отмечает М. Слифкин [4] «Дисскусии по вопросу о взаимодействиях с переносом заряда в биологии обычно бывают очень ожесточенными. Сторонники одних взглядов придают взаимодействиям с переносом заряда жизненно важное значение, сторонники других взглядов вообще не признают существования этих взаимодействий и считают их плодом воображения».
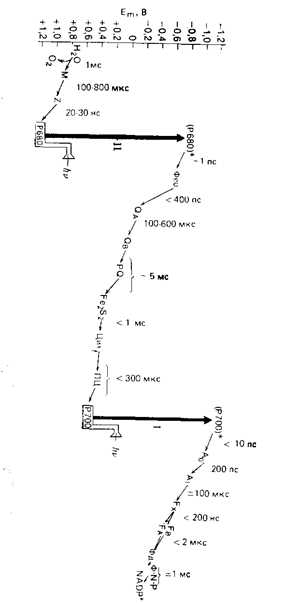
Рис. 1 – Z -схема, описывающая последовательность расположения переносчиков в электрон-транспортной цепи при фотосинтезе, сопровождающемся выделением кислорода. Показано время, необходимое для осуществления отдельных реакций; приведены также окислительно-восстановительные потенциалы средней точки Em. Воду окисляет комплекс фотосистемы II. Челночный перенос электронов от комплекса фотосистемы II к расположенному между фотосистемами комплексу цитохромов осуществляется пулом подвижного липофильного переносчика – пластохинона. Несмотря на то, что последовательность реакций переноса электронов при фотосинтезе известна, нельзя считать, что переносчики функционируют в полностью детерминированной цепи (по данным [2]).
Кроме процесса фотосинтеза в организме растения проходит процесс дыхания. Общее уравнение процесса дыхания имеет вид:
С 6 Н 12 О 6 + 6 О 2 → 6 СО 2 + 6 Н 2 О + энергия. (2)
Дыхание подразделяют на фотодыхание и дыхание поддержания [3, 5]. В отличие от фотодыхания функция истинного дыхания ясна: оно мобилизует запасенную энергию для поддержания функций биологической системы и синтеза новых структур. Однозначных ответов по поводу функции фотодыхания нет [3]. В зависимости от метода определения фотодыхания, потери, связанные с выделением СО 2 в этом процессе составляют от 15 до 40 % величины фотосинтеза. В случае методики с применением 18 О 2 на фотодыхание целого растения пшеницы при атмосферной концентрации СО 2 на полном свету приходится 50 % величины фотосинтеза [3].
Здесь, во введении хотелось бы отметить еще одну характерную черту процесса фотосинтеза. Фотосинтез – иерархический процесс, пространственная шкала которого простирается от 10-27 до 105 м3, а временная – от 10-15 (первичные фотоакты) до 10 с (первичная продуктивность в полевых условиях) [3]. В такой иерархии можно проследить цепочку уровней, которые постепенно повышаются: квант света+хлорофилл – тилакоид – хлоропласт – клетка (как наименьшая структурная единица живого) – лист (орган) – организм (единое целое) – агроэкосистема (для сельскохозяйственных культур) - … - биосфера. На каждом из этих уровней на проходящие в них процессы существенное влияние оказывают факторы внешней среды. К наиболее подвижным факторам отнесем факторы света, тепла, влаги, питания, считая остальные факторы либо значительно инерционными либо постоянными (например – гравитация). Реакция на изменение напряженности того либо иного фактора проходит на каждом уровне иерархии и, при этом мы можем отметить значительную устойчивость проходящих процессов в рамках толерантности факторов внешней среды.
На основании такого краткого изложения проблемы, возникает вопрос: существует ли фактор способный объединить или «работать» на каждом из выделенных уровней иерархии? Ответ на этот вопрос открыт. Мы здесь предложим свой взгляд на эту проблему, поэтому целью данной работы является объединение иерархических уровней растения одним фактором, хорошо известным в науке.
Объекты и выходные материалы исследования. К объекту исследования мы относим временные процессы, проходящие в организме растения. Такой объект исследования как время мы не можем «увидеть», мы можем лишь констатировать события и вычислять.
Материалы и методы исследования. Рассмотрение поставленного вопроса начнем с установленных фактов. В агрометеорологии хорошо известен метод сумм эффективных температур (Шиголев А.А.), который однозначно говорит о том, что скорость прохождения фенофаз зависит от напряженности температурного фактора [6, 7]. Согласно этому методу, чем выше напряженность температурного фактора, тем быстрее наступает очередная фенофаза. То есть с повышением уровня фактора тепла развитие растений идет быстрее. Таким образом, метод сумм эффективных температур является первым методом, который рассчитывает биологическую шкалу времени только время в нем измеряется не секундами, а градусами Цельсия. Для перехода в этом методе к единицам времени достаточно нормировать всю шкалу по отношению к константе сумм эффективных температур, которая необходима для прохождения всего онтогенеза. Тогда сразу же однозначно мы получаем в ответ, что биологическое время имеет свойство растягиваться или сжиматься в зависимости от напряженности температурного фактора. Более поздние исследования, например Улановой Е.С. [8], показывают, что скорость развития растений зависит так же от напряженности фактора влаги, рис. 2. Зависимость скорости развития растений от напряженности фактора влаги аналогична зависимости скорости развития растений от напряженности фактора тепла. Обобщением таких исследований является работа В.П. Дмитренко [9] в которой скорость развития растений зависит от напряженности факторов света, тепла, влаги, питания. Рассматривая наступление фенологических фаз развития растений как наступление определенных, биологических событий, проходящих в организме растения, мы можем заключить, что шкала биологического времени растягивается или сжимается в зависимости от движений факторов света, тепла, влаги, питания, то есть от основных, наиболее подвижных факторов внешней среды. Согласно такому подходу можно прогнозировать, что длительность межфазных периодов будет зависеть так же и от остальных, не учтенных факторов внешней среды при их движении.
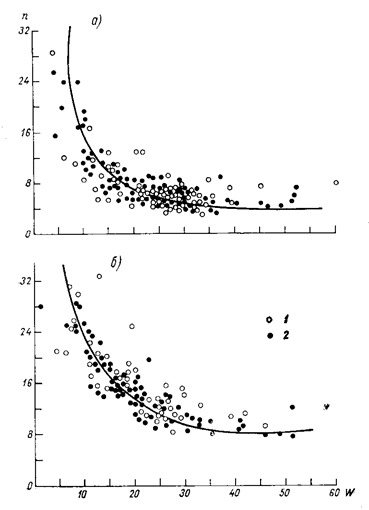
Рис. 2 – Зависимость продолжительности n дней периодов посев – всходы (а) и всходы - кущение (б) озимой пшеницы и озимой ржи от запасов продуктивной влаги пахотного слоя почвы W мм при оптимальной температуре воздуха (выше 14 оС) (по данным [8]).
Более целесообразно рассматривать в качестве биологических событий, происходящих в организме растения, не фенологические фазы развития, а наступление этапов органогенеза. Так, Ф.М. Куперман [10] в цикле онтогенеза выделяет XII этапов органогенеза на примере озимой пшеницы, ржи и других зерновых колосовых культур, рис. 3. Этапы органогенеза связываются с деятельностью меристематической ткани в конусе нарастания надземного побега. На каждом этапе органогенеза выдвигаются свои требования к состоянию факторов внешней среды. В этом смысле можно говорить об оптимальных значениях факторов света, тепла, влаги, питания для каждого этапа органогенеза. То есть, требования к состоянию факторов внешней среды для того либо иного вида, сорта растений имеют свое движение на протяжении онтогенеза, при последовательной смене одного этапа развития за другим. Тогда длительность каждого этапа органогенеза определится напряжением складывающихся, наиболее значимых факторов внешней среды и требованиями к их оптимальности на каждом этапе.

Рис. 3 – Фазы развития и XII этапов органогенеза озимой пшеницы (данные из [8]).
Исходя из таких представлений, становится ясно, что существуют как минимум две шкалы времени: физическое или календарное время, по отношению к которому мы фиксируем события, проходящие в организме растения и биологическое время, которое растягивается или сжимается по отношению к физическому времени. При этом, по отношению к системе отсчета, связанной с организмом растения, биологическое время всегда движется равномерно. Мы предлагаем рассмотреть движения биологического времени на уровне целого организма растения. Временные процессы мы будем связывать с материальными процессами организма растения: ростом живой биомассы, фотосинтезом, дыханием. То есть, мы будем рассматривать биологическое время по отношению к массе организма растения, по отношению к величине выхода фотосинтеза, по отношению к величине фотодыхания и дыхания поддержания. Все эти величины тем либо иным способом могут быть измерены экспериментально или расчитанны на основе длиннопериодных динамических моделей продукционного процесса растений, которые позволяют рассматривать перечисленные процессы в динамике за весь онтогенез с учетом влияния факторов внешней среды [11, 12, 13, 14, 15].
Общая биомасса целого организма растения складывается из приростов биомассы за каждый шаг роста. Временная величина шага является бесконечно малой величиной, поэтому уравнение роста биомассы, в общем виде записывается следующим образом
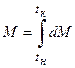 , (3)
, (3)
где М – общая биомасса посева растений; dM – прирост биомассы за бесконечно малый шаг роста; tн – момент начала роста; tк – момент завершения роста.
Дифференциальная форма этого уравнения, согласно исследованиям [16] имеет вид
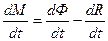 , (4)
, (4)
где 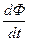 - скорость процесса фотосинтеза растений;
- скорость процесса фотосинтеза растений; 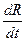 - скорость процесса дыхания растений; t – физическое время. Дифференциальная форма (4) показывает, что прирост общей сухой биомассы посева растений определяется его газообменом: балансом процессов фотосинтеза и дыхания целого организма растения. Как мы уже отмечали, существует две системы отсчета времени, поэтому в уравнении (4) (а также (3)) будем рассматривать процессы фотосинтеза и дыхания по отношению к биологической оси времени
- скорость процесса дыхания растений; t – физическое время. Дифференциальная форма (4) показывает, что прирост общей сухой биомассы посева растений определяется его газообменом: балансом процессов фотосинтеза и дыхания целого организма растения. Как мы уже отмечали, существует две системы отсчета времени, поэтому в уравнении (4) (а также (3)) будем рассматривать процессы фотосинтеза и дыхания по отношению к биологической оси времени
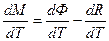 , (5)
, (5)
где Т – биологическое время. Правомерность такой замены шкалы времени обеспечивается тем, что ранее такая замена уже была осуществлена на основе метода сумм эффективных температур А.Н.Полевым [13] при расчете логистической кривой роста и других процессов растений. Если рассматривать фотосинтез и дыхание как два противоположных, равноправных процесса, уравнения (1) и (2), то мы уже получаем пространство двух переменных биологического времени. То есть, мы можем рассматривать двухмерное временное многообразие вложенное, например, в трехмерное пространство. При этом первая переменная времени относится к процессу фотосинтеза, а вторая переменная времени относится к процессу дыхания. При исследовании уравнений (3) и (5) мы будем использовать аппарат дифференциальных форм, изложенный в работах [17, 18, 19]. Мы будем рассматривать дифференциальную форму dM, то есть приросты общей сухой биомассы. Эта форма определяется балансом процессов газообмена: фотосинтеза и дыхания. Согласно теореме Стокса для областей с регулярной границей [19] мы можем записать
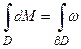 , (6)
, (6)
где D – временная область определения дифференциальной формы dM; ∂D - регулярная граница временной области. Если рассматривать самый простой, тривиальный случай в этом уравнении, то по формуле Ньютона-Лейбница мы получаем уравнение (3), где временная область D представляет собой ориентируемый отрезок биологического времени от начала роста до его завершения. Концевые точки этого отрезка являются его границей ∂D, а внутренность отрезка – областью определения. В таком случае нет подразделения формы dM на составляющие её процессы и для расчета по такому уравнению мы должны ввести в рассмотрение логистическую кривую роста общей сухой биомассы растений и по отношению к таковой рассматривать процессы биологического времени.
В двухмерном случае уравнения (6) мы однозначно получаем подразделение формы ω на процессы фотосинтеза и дыхания по формуле Грина [19]
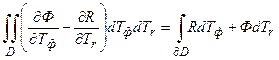 , (7)
, (7)
где Тф – первая координата биологического времени для процесса фотосинтеза; Тr – вторая координата биологического времени для процесса дыхания. По уравнению (7) мы получили подразделение приростов общей сухой биомассы dM на процессы фотосинтеза и дыхания, определяющие её газообмен. Такое подразделение обеспечивается существованием биологического двухмерного временного образования. В левой части уравнения (7) мы видим тот процесс газообмена, который мы фиксируем в экспериментальных исследованиях, при этом существенна противоположная направленность этих двух процессов. В правой части уравнения (7) мы видим, что фотосинтез и дыхание – это два одинаковых процесса для системы отсчета, связанной с организмом растения. Таким образом, процессы фотосинтеза и дыхания тесно взаимосвязаны процессами течения биологического времени. При этом, по уравнению (7) ясно, что двухмерное временное многообразие (например, временная поверхность) вложено в двухмерное временное пространство, например в R2. Заметим, что по уравнению (7) нет подразделения процесса дыхания на его составляющие, а как мы знаем, процесс дыхания подразделяется на дыхание поддержания и фотодыхание [20]. По этому уравнению (7) процесс фотосинтеза и процесс дыхания – это функции координат биологической временной точки: Ф(Тф, Тr), R(Tф, Тr). На этом основании мы можем изучать процессы биологического времени на основе течения процессов фотосинтеза и дыхания в онтогенезе растений в пространстве R2.
Рассмотрим трехмерный случай уравнения дифференциальной формы (6), при этом будем опираться на линейную дифференциальную форму в евклидовом временном пространстве [18]
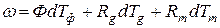 , (8)
, (8)
где Ф – процесс (функция) фотосинтеза; Rg – процесс (функция) дыхания роста; Rm – процесс (функция) дыхания поддержания; Т – точка биологического временного пространства Т=(Тф, Тg, Tm). Здесь, как и прежде имеет значение номер, порядок биологических временных координат. Можно считать, что функции Ф, Rg, Rm, изменяющиеся в онтогенезе, определяют вектор
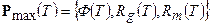 , (9)
, (9)
где функции фотосинтеза Ф(Т), фотодыхания Rg(T), дыхания поддержания Rm(T) являются функциями биологической временной точки Т=(Тф, Тg, Tm). Вектор P max(T) соответствует принципу максимальной продуктивности Х.Г. Тооминга [21]:
Fc(L, t) → max, (10)
где Fc(L, t) – газообмен СО 2 посева растений. Согласно принципу максимальной продуктивности, адаптация растений и фитоценоза направлена на обеспечение максимально возможного газообмена СО 2 в данных условиях среды. Отметим, что вектор P max(T) закономерно изменяется в течении онтогенеза в соответствии с определяющими его процессами течения биологического времени и поэтому обеспечивает максимальный газообмен растения.
Теперь проведем внешнее дифференцирование формы ω (8), тогда мы получим формулу Стокса для двухмерного временного биологического многообразия, вложенного в трехмерное биологическое временное пространство
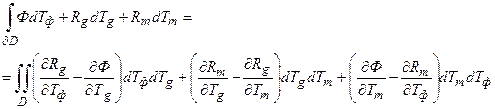 (11)
(11)
где ∂D – гладкая временная кривая во временном пространстве, ограничивающая временную поверхность; D – временная поверхность во временном пространстве. При таком подходе, мы рассматриваем внутреннее временное пространство организма растения.
То есть мы получили ротор (вихрь) вектора P max(T)

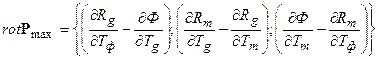 , (12)
, (12)
который показывает поток временного векторного поля через элементарную временную площадку. Если рассматривать величины Ф, Rg, Rm все в нормированном виде тогда ротор rot P max покажет изменения движения биологического временного поля для целого организма растения в онтогенезе.
Полученное уравнение (11) говорит о том, что процессы фотосинтеза, фотодыхания и дыхания поддержания для системы отсчета, связанной с организмом растения, просто соотносятся друг с другом как одно целое (левая часть уравнения (11)). Движение биологического времени идет по замкнутой траектории и это движение времени обеспечивает цельную систему трех процессов. Правая часть уравнения (11) показывает подразделение цельной системы на три процесса: фотосинтез, фотодыхание и дыхание поддержания. Правая часть уравнения (11) – это то, что мы наблюдаем в экспериментальных исследованиях растений. Согласно уравнению (11) становится ясна роль фотодыхания и дыхания поддержания – наряду с фотосинтезом эти процессы обеспечивают вращение биологического временного поля в организме растения.
Полученное соотношение (11) говорит о том, что процессы фотосинтеза и дыхания (газообмена) однозначно определяют скорость течения биологического времени, или, точнее наоборот – движения биологического временного поля обеспечивает свое проявление как процесс фотосинтеза, фотодыхания и дыхания поддержания для случая трехмерного пространства. Отметим так же и то, что согласно исследованиям И.А. Аршавского [22] существует «энергетическое правило поверхности», то есть в организме растения присутствует некоторая поверхность. Более того, при таких временных изменениях нельзя ожидать выполнения классических физических законов. Вывод, сделанный И.А. Аршавским подтверждает это: «Данные наших исследований позволили прийти к заключению, что живые системы не подчиняются не только законам равновесной, но и неравновесной термодинамики. Более того, живые системы вообще не подчиняются второму принципу термодинамики» [22].
Теперь приведем систему дифференциальных уравнений электромагнитного поля согласно теории Максвелла [23, 24, 25]:
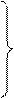 1.
1. 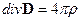 , 2.
, 2. 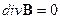 ,
,
(13)
3. 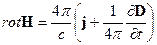 , 4.
, 4. 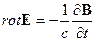 ,
,
исходя их которых, электромагнитное поле в каждой точке в каждый момент времени определяется четырьмя величинами: векторами H и D, характеризующими электрическое поле, и векторами E и B, характеризующими магнитное поле. В уравнениях электромагнитного поля, помимо этих четырех векторов, фигурируют еще две величины: плотность заряда ρ и плотность тока j; они характеризуют источники поля – заряды и токи, наличие которых приводит к возбуждению поля в окружающем пространстве,(см. [23, 24, 25]). При этом здесь с – скорость света в пустоте, равная 2.998·1010 см/с ≈ 3·1010 см/с. Приведенная система уравнений справедлива для электромагнитных полей в любых средах. Эти уравнения дополняются материальными уравнениями, учитывающими соотношение между векторами E, D, B, H и j. Можно записать эти уравнения при помощи трех констант σ (электропроводность), ε (диэлектрическая проницаемость) и μ (магнитная проницаемость):
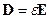 ,
, 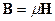 ,
, 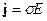 . (14)
. (14)
Таким образом, система уравнений (13) вместе с материальными уравнениями (14) описывают макроскопическое электромагнитное поле.
Нам остается сопоставить полученный ротор биологического временного поля (12) с уравнениями 3 и 4 системы уравнений Максвелла (13):
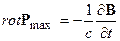 . (14)
. (14)
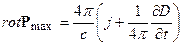 . (15)
. (15)
Эти уравнения описывают вихрь биологического временного поля в зависимости от приходящего электромагнитного поля на различных уровнях иерархии организма растения. При этом, свет попадает в такую ловушку как вихрь биологического временного поля. Таким образом, с учетом теории Максвелла мы можем так же рассчитать вихрь биологического временного поля и таким способом.
Результаты исследования и их анализ. На основе динамической модели продукционного процесса подсолнечника [26] мы получили оценки фотосинтеза Ф, фотодыхания Rg, и дыхания поддержания Rm, закономерно изменяющиеся в онтогенезе подсолнечника. Отметим, что величины Ф, Rg, Rm являются не скоростями, а интегральными характеристиками рассматриваемых процессов. Кроме того, мы нормировали величины Ф, Rg, Rm по отношению к максимальной величине Ф и построили годограф вектора P max(T) (9) для трехмерного временного пространства организма растения, рис. 4. Годограф вектора P max(T) показывает изменения этого вектора в онтогенезе, если его начало отложить от нулевой точки системы биологических временных координат. На основании полученных данных, рис.4, можно заключить, что происходит поступательное и вращательное движение биологического временного поля в течении онтогенеза растения. Скорости этих движений зависят от генотипа растения и напряженности факторов внешней среды.
Физический смысл ротора биологического временного поля можно пояснить следующим образом. Рассмотрим векторное поле биологического времени как поле скоростей движущейся жидкости. Поместим в таком потоке, в определенной его точке, бесконечно малое колесико с лопастями. Под воздействием потока такое колесико будет вращаться с некоторой скоростью. Будем считать такое колесико бесконечно малым. Тогда, на основании [27], скорость вращения биологического временного поля будет равна:
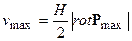 , (13)
, (13)
где vmax – линейная скорость вращения колесика, то есть вращения биологического временного поля; H – конечный радиус колесика.
Но vmax/H – это величина угловой скорости z колесика. Тогда полученный ротор биологического временного поля (12) определяет удвоенную угловую скорость вращения колесика, то есть углового вращения временного поля в данной биологической временной точке
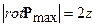 . (14)
. (14)
Угловое вращение биологического временного поля рассматривается как вращение некоторого вектора скорости движения поля. При этом, с постоянным движением физического времени и прохождения процессов фотосинтеза и двух составляющих дыхания будет меняться ротор rot P max.
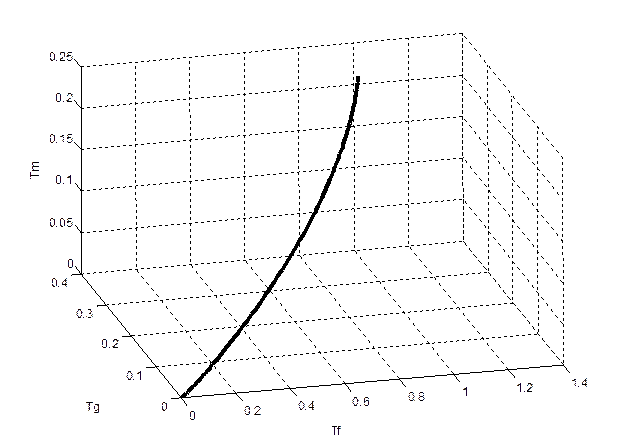
Рис. 4 - Годограф ротора биологического временного поля в онтогенезе подсолнечника для среднемноголетних агрометеорологических условий Одесской области:
Tf – биологическая временная координата фотосинтеза; Tg – биологическая временная координата фотодыхания; Tm – биологическая временная координата дыхания поддержания.
Выводы. На основании данной работы можно сделать заключение, что поступающие электромагнитные волны (свет) попадают в ловушку колеблющегося биологического временного поля внутри организма растения. Здесь можно говорить о различных видах колебательного процесса биологического временного поля.
Список литературы
- Мусієнко М.М. Екологія рослин. – Київ: „Либідь”, - 2006, - 431 С.
- Фотосинтез. Под ред. Говинджи. – Москва: „Мир”, - 1987, Т. 1, - 727 С.
- Фотосинтез. Под ред. Говинджи. – Москва: „Мир”, - 1987, Т. 2, - 470 С.
- Слифкин М. Роль взаимодействий с переносом заряда в биологии. В кн..: Молекулярные взаимодействия. – Москва: „Мир”, - 1984, - С. 272 – 305.
- Полевой В.В. Физиология растений. – Москва: „Высшая школа”, - 1989, - 464 С.
- Руководство по агрометеорологическим прогнозам. – Ленинград: Гидрометеоиздат, - 1984, Т. 1, - 309 С.
- Руководство по агрометеорологическим прогнозам. – Ленинград: Гидрометеоиздат, - 1984, Т. 2, - 264 С.
- Уланова Е.С. Агрометеорологические условия и урожайность озимой пшеницы. – Ленинград: Гидрометеоиздат, - 1975, - 302 С.
- Дмитренко В.П. О совместном учете влияния факторов внешней среды на продолжительность межфазных периодов растений. // Труды УкрНИГМИ, - 1987, Вып. 223, С. 3 – 23.
- Куперман Ф.М., Дворянкин Ф.А., Ростовцева З.П., Ржанова Е.И. Этапы формирования органов плодоношення злаков. Из-во Московського университета, - 1955, - 319 С.
- Галямин Е.П. Оптимизация оперативного распределения водных ресурсов в орошении. – Ленинград: Гидрометеоиздат, - 1981, - 272 С.
- Сиротенко О.Д. Математическое моделирование водно-теплового режима и продуктивности агроэкосистем. – Ленинград: Гидрометеоиздат, - 1981, - 167 С.
- Полевой А.Н. Теория и расчет продуктивности сельскохозяйственных культур. – Ленинград: Гидрометеоиздат, - 1983, - 175 С.
- Франс Дж., Торнли Дж.Х.М. Математические модели в сельском хозяйстве. – Москва: Агропромиздат, - 1987, - 400 С.
- Моделирование роста и продуктивности сельскохозяйственных культур. Под ред. Ф.В.Т. Пеннинга де Фриза и Х.Х. ван Лаара. – Ленинград: Гидрометеоиздат, - 1986, - 320 С.
- Davidson J.L., Philip J.R. Light and pasture growth. –In.: Climatology and microclimatology. UNESCO, 1958, P.181-187.
- Арнольд В.И. Математические методы классической механики. – Москва: «Наука», - 1989, -472 С.
- Ефимов Н.В. Введение в теорию внешних форм. – Москва: «Наука», - 1977, -86 С.
- Постников М.М. Гладкие многообразия. – Москва: «Наука», - 1987, -478 С.
- McCree K.J. An equation for the rate of respiration of white clover plants grown under controlled condition. –In.: Prediction and measurement of photosynthetic productivity. - Wageningen: 1970, P.221-229.
- Тооминг Х.Г. Экологические принципы максимальной продуктивности посевов. – Ленинград: Гидрометеоиздат, - 1984, -264 С.
- Аршавский И.А. Механизмы онто - и гетерогенеза. // Онтогенез, 1995, т. 26, № 6, С.481-488.
- Тамм И.Е. Основы теории электричества. – Москва: „Наука”, - 1989, - 504 С.
- Калитеевский Н.И. Волновая оптика. – Москва: „Наука”, - 1971, - 376 С.
- Вайнштейн Л.А. Электромагнитные волны. – Москва: „Радио и связь”, - 1988, - 440 С.
- Наумов М.М. Динамическая модель продукционного процесса подсолнечника. // Метеорология и гидрология, - 2006, № 6, С. 104 -110.
- Будак Б.М., Фомин С.В. Кратные интегралы и ряды. – Москва: «Наука», - 1967, -607 С.
Date: 2015-09-05; view: 447; Нарушение авторских прав