
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод наименьших квадратов для построения линии регрессии
|
|
Этап 3. Нахождение взаимосвязи между данными
Обычно при анализе связи между двумя случайными величинами желательно одну из них (скажем, Х) считать независимой, а другую (Y) – зависимой. Задача заключается в установлении такой связи между предиктором Х и предиктантом Y, которая позволила бы получить значения 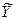 с наименьшей ошибкой.
с наименьшей ошибкой.
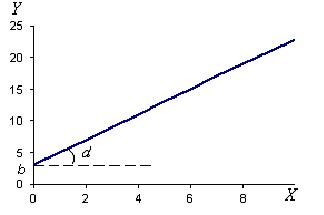
Простейшим является случай, когда двумерное распределение или точечная диаграмма указывает на линейную связь между Х и Y. Тогда выражение 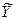 = a + bX будет хорошо удовлетворять исходным данным и будет называться линией регрессии. Прямую регрессии можно провести на глаз так, чтобы она как можно ближе проходила около средних значений различных столбцов (при условии, что Х нанесено по горизонтали, а Y – по вертикали).
= a + bX будет хорошо удовлетворять исходным данным и будет называться линией регрессии. Прямую регрессии можно провести на глаз так, чтобы она как можно ближе проходила около средних значений различных столбцов (при условии, что Х нанесено по горизонтали, а Y – по вертикали).
Наиболее часто для оценки коэффициентов линии регрессии используется метод наименьших квадратов. Этот метод был разработан в начале XIX в. в трудах Лежандра, Лапласа и Гаусса и применен ими для решения метрологических проблем астрономии и геодезии. Согласно определению, сумма квадратов отклонений отдельных величин Yi от значений, предсказываемых с помощью линии регрессии, является минимальной.
Пусть есть n пар значений случайных величин (Xi, Yi), n > 2. Известно, что между этими случайными величинами существует линейная зависимость 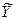 = kX+b. Константы этой функции a и b надо определить аналитически. При этом требуется, чтобы разность между отдельными значениями случайной величины Yi и значениями
= kX+b. Константы этой функции a и b надо определить аналитически. При этом требуется, чтобы разность между отдельными значениями случайной величины Yi и значениями 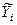 , вычисленными из уравнения, была возможно меньше, т.е. отыскивается наиболее оптимальная функция. Следовательно, рассеяние точек относительно линии регрессии должно быть меньше, чем относительно любой другой прямой.
, вычисленными из уравнения, была возможно меньше, т.е. отыскивается наиболее оптимальная функция. Следовательно, рассеяние точек относительно линии регрессии должно быть меньше, чем относительно любой другой прямой.
Коэффициенты регрессии вычисляются по формулам:
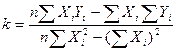 , (1)
, (1)
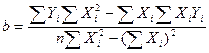 . (2)
. (2)
Иногда коэффициентом регрессии называют только угловой коэффициент k, т.к. зная его можно определить отрезок b, отсекаемый линией регрессии по оси ординат. При этом используется весьма важное свойство линии регрессии, что она проходит через среднюю точку (центр) двумерного распределения  лежащую при значениях
лежащую при значениях 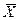 и
и 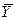 .
.
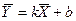 ,
, 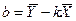 ,
,
или
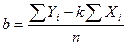 (3)
(3)
|
Величины k и b являются статистическими параметрами, полученными из выборки, а не параметрами генеральной совокупности. На практике желательно знать, насколько репрезентативна для будущих данных, взятых из генеральной совокупности, полученная из выборки линия регрессии (т.е. насколько точным будет прогноз, составленный с помощью такого уравнения регрессии). С помощью статистической теории можно показать, в какой степени величины k и b отражают соответствующие параметры генеральной совокупности. В общем, чем больше наблюдений и чем меньше разброс точек относительно линии регрессии, тем надежнее величины k и b.
Степень несогласованности (разброса) наблюдаемых значений случайных величин и линией регрессии может быть оценена с помощью величины дисперсии, определяемой по формуле:
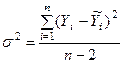 . (4)
. (4)
Здесь число степеней свободы f = n – 2, т.к. две степени свободы были использованы для определения параметров прямой.
Обычно вычисление дисперсии производят, пользуясь формулой, большая часть членов в которой подсчитывается при определении параметров линии регрессии:
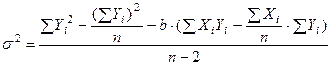 , (5)
, (5)
или 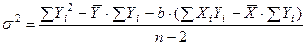 .
.
Мы рассмотрели примеры аппроксимации дискретных рядов случайных величин. Можно аппроксимировать и интервальные (сгруппированные) ряды случайных величин. Исходные данные в этом случай группируются с частотами mx,y. На их основе, используя центральные значения каждой градации, рассчитываются групповые параметры S Y, S X, S X2, S XY, которые затем используются в формулах (1)-(2) для определения коэффициентов регрессии методом наименьших квадратов. Линия регрессии в этом случае конечно будет хуже отражать закономерности связи по сравнению с дискретными измерениями.
| <== предыдущая | | | следующая ==> |
| | | Особливості економічного розвитку та загальна характеристика господарства |
Date: 2015-09-05; view: 360; Нарушение авторских прав