Решите задачу (7 баллов). Муниципальный этап олимпиады школьников

Муниципальный этап олимпиады школьников

По математике 2012-2013 учебный год

Класс

Максимальный балл – 35

Решите задачу (7 баллов)

На доске написано 4 9 2 5 2 1=100. Поставьте между некоторыми цифрами знаки сложения и вычитания, чтобы получилось верное равенство.

Решение. 4+92+5–2+1=100.

Оценивание. За верный пример – 7 баллов.

Решите задачу (7 баллов)

Сколько раз в сутки часовая и минутная стрелки образуют прямой угол?

Решение. В сутки часовая стрелка делает два оборота, а минутная – 24 (на 22 оборота больше). В течение каждого такого оборота есть единственный момент времени, когда стрелки образуют развернутый угол.

Ответ: 22

Оценивание. За верное решение – 7 баллов.

Решите задачу (7 баллов)

Даны три натуральных числа. Для каждых двух из них вычислили наибольший общий делитель и наименьшее общее кратное. Полученные шесть чисел сложили. Могло ли получиться число12345?

Решение. Заметим, что НОД и НОК четных чисел число чётное, а нечётных – нечётное. НОД четного и нечётного чисел – нечётное число, и их НОК – чётное число. Перебирая все случаи (три чётных числа; два чётных, одно нечётное; одно чётное, два нечётных; три нечётных), приходим к выводу, что сумма чисел, о которых говорится в условии задачи, чётна.

Ответ: нет

Оценивание. За верное решение – 7 баллов.

Решите задачу (7 баллов)

Остатки от деления натурального числа n на 10, 11, 12, …, 20 выписали в строчку. Оказалось, что каждое число, начиная со второго, больше предыдущего. Докажите, что в строчке записано 11 последовательных целых чисел.

Решение. Пусть остаток от деления числа n на 20 равен r. Это означает, что для некоторого целого числа q выполнено равенство n=20q+r, где 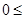r<20. Если r<10, остаток от деления n на 10 будет равен также r, что противоречит условию задачи. Значит, r 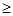10 и n=10·(2q+1)+(r – 10). Поскольку 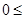r – 10<10, число (r – 10) является остатком от деления n на 10. В возрастающей последовательности 11 целых чисел, последнее число на 10 больше первого – это говорит о том, что числа идут подряд (иначе разность последнего и первого числа была бы больше 10).

Оценивание. За верное решение – 7 баллов.

Date: 2015-09-05; view: 4380; Нарушение авторских прав