Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Информация для преподавателя
|
|
Лабораторная работа №6
Масса и энергия связи атомных ядер.
I. Цель работы: 1. Ознакомление с основными массовыми и энергетическими
характеристиками атомных ядер.
2. Изучение зависимости энергии связи ядер как функция
массового числа А и заряда Z (формула Бете – Вайцзеккера)
3. Оценка некоторых параметров стабильных, ядер а также
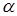 -и
-и 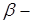 активных ядер.
активных ядер.
II. Теоретическая часть.
2.1. Основные понятия и определения:
Как известно, все стабильные и долгоживущие (t >10-10с) атомные ядра состоят из протонов (p) и нейтронов (n), которые называют иногда нуклонами. Укажем основные параметры нуклонов и, для сравнения, электрона (е) в виде таблицы 1:
Таблица 1. Основные характеристики нуклонов и электрона.
| частица | Масса (mо) | mос2 (МэВ) | электр. зар. (Кл) | ||
| (кг) | (в един. mе) | (в а.е.м.) | |||
| протон (р) |
1,6726 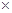 10-27 10-27
| 1836,15 | 1,007276 | 938,279 |
+1,602 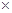 10-19 10-19
|
| нейтрон (n) |
1,6749 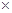 10-27 10-27
| 1838,68 | 1,008665 | 939,573 | |
| электрон (е) |
9,1105 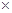 10-31 10-31
|
5,48 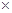 10-4 10-4
| 0,511 |
-1,602  10-19 10-19
|
В таблице указана одна из внесистемных единиц измерения массы микрочастиц - атомная единица массы (а.е.м.). За 1 а.е.м. принимается 1/12 часть массы нейтрального атома изотопа углерода 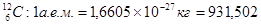 МэВ.
МэВ.
Если в состав ядра входит Z протонов и N нейтронов, то их общее число А=Z+N называется массовым числом или барионным зарядом. Каждое ядро обозначается в виде 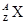 , где X – символ соответствующего химического элемента.(
, где X – символ соответствующего химического элемента.(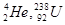 ).Ядра с одинаковыми
).Ядра с одинаковыми 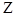 и разными А называются изотопами; ядра с одинаковыми А и разными
и разными А называются изотопами; ядра с одинаковыми А и разными 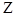 - изобарами; ядра с одинаковыми N и разными
- изобарами; ядра с одинаковыми N и разными 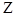 - изотонами. Два изобарных ядра, отличающие заменой р
- изотонами. Два изобарных ядра, отличающие заменой р 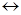 n называются зеркальными (
n называются зеркальными ( F).
F).
Важнейшим параметром ядра 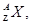 характеризующим его прочность, является энергия связи Есв (Z,A).
характеризующим его прочность, является энергия связи Есв (Z,A).
Энергия связи ядра ( относительно всех нуклонов) называется минимальная энергия, которую необходимо сообщить ядру, чтобы полностью расщепить его на составляющие его нуклоны. Заметим, что внутренняя энергия ядра Евн отличается от энергии связи знаком Евн=-Есв. Знание энергий связи ядер позволяет рассчитать энергетический баланс не только для процесса полного расщепления, но и для любых процессов распадов и взаимных превращений ядер. Например, энергия отделения протона Ер от ядра 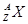 равна:
равна:
Ер=Есв(Z, A) - Есв(Z-1, А-1). (1)
Энергия «прилипания» нейтрона к ядру Еn равна:
Еn=Есв(Z, А) – Есв(Z, А+1). (2)
Для выбивания из ядра 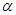 -частицы (ядро
-частицы (ядро 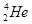 ) нужна энергия:
) нужна энергия:
Е2=Есв(Z, A) - Ecв(Z-2, A-4) – Есв(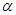 ). (3)
). (3)
Удельной энергией связи ядра называется отношение 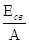 .
.
В силу известного соотношения между массой и энергией (Е=Мс2) Есв можно записать в виде:
Есв=[ZMр+NMn-M(Z,A) ] c2, (4)
если масса выражена в кг..Если масса выражена в энергетических еденицах (когда указана фактически энергия покоя М0с2), то равенство (4) запишется в виде:
Есв=ZMp+NMn-M(Z,A) (5)
Массы заряженных частиц экспериментально измеряют с помощью масс-спектрографов, с относительной точностью 10-5-10-6 (или по энергии связи ~ 0,01%).
Для практических целей важно отметить, что в справочных таблицах приводятся не массы ядер, а массы соответствующих нейтральных атомов. Поэтому для удобства вычислений в (5) добавим и вычтем массу Z электронов атома и, пренебрегая разницей энергий связи электронов в Z атомах водорода и в атоме 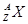 , получаем:
, получаем:
Есв(Z,A)=ZMaт(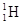 )+NMn-Mат(
)+NMn-Mат(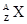 ). (6)
). (6)
Из соотношения (4) и (5) следует, что масса стабильного ядра (Есв 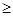 0) меньше суммы масс отдельных нуклонов на величину Есв (либо
0) меньше суммы масс отдельных нуклонов на величину Есв (либо 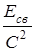 ), которая определяется путём введения понятия дефекта массы ядра.
), которая определяется путём введения понятия дефекта массы ядра.
Дефектом массы ядра в ядерной физике называется разность между массой ядра, выраженной в а.е.м. и соответствующим массовым числом:
 ∆(Z,A)=Mя(Z,A)-A (7)
∆(Z,A)=Mя(Z,A)-A (7)
В частности, из таблицы 1 дефект массы р и n равны ∆р=0,007276а.е.м.=6,77761МэВ
∆n=0,008665а.е.м.=8,07146МэВ
Для 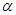 -частицы (по справочным данным) ∆
-частицы (по справочным данным) ∆ 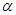 =0,001506=1,40284МэВ.
=0,001506=1,40284МэВ.
Для установления зависимости дефекта массы и энергии связи ядра учтем условие (6), где массы выражены в а.е.м., и соотношение (7), т.е.  Mя=∆+A, Mр=∆р+1, Mк=∆к+1.
Mя=∆+A, Mр=∆р+1, Mк=∆к+1.
Есв=Z(∆р+1)+N(∆n+1)-(∆+A)= Z∆р+N∆n-∆(Z,A). (8)
Например, для 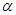 -частицы (
-частицы (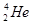 ) имеем:
) имеем:
Есв=2 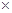 (0,007276+0,008665)-0,001506=0,0030 а..е.м.=28,38МэВ.
(0,007276+0,008665)-0,001506=0,0030 а..е.м.=28,38МэВ.
В справочных таблицах обычно приводятся не массы ядер, а массы (дефекты массы) нейтральных атомов, которые больше масс ядер на массы электронных оболочек. Естественно дефекты массы нейтральных атомов определить соотношением:
δ(Z,A)= Mаг(Z,A)-А. (9)
Например δ(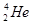 )=∆
)=∆ 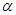 +2
+2 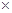 ∆ е=0,001506+2
∆ е=0,001506+2 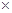 0,000549=0,002604 а.е.м.=2,42563МэВ
0,000549=0,002604 а.е.м.=2,42563МэВ
Очевидно, формула (8) остается справедливой, если дефекты масс ядер заменить на дефекты масс нейтральных атомов:
Есв = Zδм + Nδn –δ(Z,А) (10)
(здесь δn = ∆n). Дефекты масс всех атомов с 0 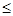 Z
Z 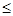 94 приведены в приложении 1.
94 приведены в приложении 1.
2.2. Полуэмпирическая формула Бете-Вайцзеккера (БВ):
Важнейшей задачей ядерной физики является получение зависимость Есв= Есв (Z,A) из всей совокупности ядерно-физических данных. Для получения этой зависимости важнейшими являются пять признаков.
1. Для не слишком легких ядер (А 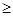 20) удельная энергия связи примерно постоянна и составляет около 8 МэВ/нуклон. Этот т.н. объемный член можно записать в виде:
20) удельная энергия связи примерно постоянна и составляет около 8 МэВ/нуклон. Этот т.н. объемный член можно записать в виде:
Е1 = а1 А (11)
Эта линейная зависимость от А свидетельствует о свойстве насыщения ядерных сил и их короткодействующем характере. С насыщением ядерных сил связано и то обстоятельство, что плотность ядерного вещества для не слишком легких ядер приблизительно постоянна. Для грубых оценок можно записать:
 .
.
Отсюда находим зависимость “радиуса” ядра от А:
R = R0 А⅓, (12)
где по разным данным R0 = (1,2-1,5) 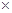 10-15 м.
10-15 м.
2. Спад зависимости Есв(A) при малых А можно качественно объяснить в т.н. жидко-капельной модели, в которой атомное ядро рассматривается как капля несжимаемой положительно заряженной “жидкости”. Нуклоны на “поверхности” этой капли испытывают меньшее притяжение, чем внутри объема, что должно приводить к уменьшению энергии связи Епов = - σ S ~ R2 ~ A2/3, где σ – “коэффициент поверхностного натяжения” ядерной материи, S – площадь поверхности ядра. Таким образом, поверхностная энергия должна описываться формулой вида:
E2 = -a2 A2/3 (13)
3. Небольшое уменьшение энергии связи (~1Мэв/нукл) в области тяжелых элементов можно объяснить возрастанием роли кулоновского отталкивания между протонами. Эта кулоновская энергия должна зависеть от Z и A следующим образом:
Екул ~ 
 или Ез = - а3
или Ез = - а3 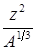 (14)
(14)
4. Из таблицы Менделеева следует, что для легких и средних ядер (А 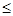 40) число протонов и нейтронов в ядре совпадает, т.е. N=Z (A-2Z=0), а тяжелые ядра перегружены нейтронами, так что в области трансурановых элементов N=1,6Z, А=2,6 Z. Считается установленным, что в отсутствии кулоновских сил, наиболее прочными были бы ядра при равном числе протонов и нейтронов. качественно это можно объяснить действием принципа запрета Паули. Эта энергия симметрии может быть приближенно описана членом вида:
40) число протонов и нейтронов в ядре совпадает, т.е. N=Z (A-2Z=0), а тяжелые ядра перегружены нейтронами, так что в области трансурановых элементов N=1,6Z, А=2,6 Z. Считается установленным, что в отсутствии кулоновских сил, наиболее прочными были бы ядра при равном числе протонов и нейтронов. качественно это можно объяснить действием принципа запрета Паули. Эта энергия симметрии может быть приближенно описана членом вида:
Е4 = - a4 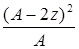 (15)
(15)
5. Прочность атомного ядра в значительной степени зависит от четности числа протонов и нейтронов в ядре. Достаточно указать распространенность стабильных ядер в природе (см. табл. 2).
Табл. 2 Распространенность стабильных ядер в природе:
| Z | N | A= Z+N | Число ядер |
| Четное Четное Нечетное Нечетное | Четное Нечетное Четное Нечетное | Четное Нечетное Нечетное Четное |
Этот факт свидетельствует о спаривании одинаковых нуклонов в ядре, при этом энергия связи возрастает на 2-3 МэВ. Разумеется эффект спаривания становится относительно менее существенным в области тяжелых ядер ~ A-1/3. Энергию спаривания качественно можно описать зависимостью вида:
Е5 = + a5 δ/ A1/3 (16)
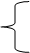 -1 (нечетно-нечетные ядра)
-1 (нечетно-нечетные ядра)
где δ = 0 (нечетные А)
+1 (четно-четные ядра)
Таким образом, приближенно зависимость Есв(Z,А) можно записать в виде:
Есв = a1А – a2A2/3 - а3 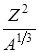 - a4
- a4 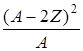 + a5 δ/ A1/3 (17)
+ a5 δ/ A1/3 (17)
Полученная зависимость называется полуэмпирической формулой Бете-Вайцзеккера (БВ). Сравнивая (17) с опытными данными можно определить постоянны a i [1]:
a1 = 15,75 МэВ; a2 = 17,80 МэВ; a3 = 0,71 МэВ; a4 = 23,7 МэВ; a5 = 12 МэВ.
3. Задания:
1. Изучить теорию. Дать ответы на контрольные вопросы.
2. Решить следующие задачи:
2.1. Дефект массы атома 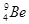 равен δ (Z,А)= δ (4,9) = 11,3484 МэВ. Определить энергию связи ядра
равен δ (Z,А)= δ (4,9) = 11,3484 МэВ. Определить энергию связи ядра 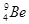 относительно распада его на две
относительно распада его на две 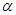 -частицы и нейтрон. Как можно использовать полученный результат для практических целей?
-частицы и нейтрон. Как можно использовать полученный результат для практических целей?
2.2 Используя дефекты масс δ (1,2) = 13,13627 МэВ, δ (1,3) = 14,95038 МэВ, δ (2,3) = 14,93173 МэВ, вычислить энергию Q, выделяющуюся в следующих термоядерных реакциях:
a) 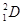 +
+ 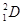 →
→ 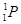 +
+ 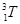 ; б)
; б) 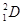 +
+ 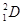 →
→ 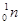 +
+ 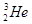 ;
;
в) 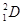 +
+ 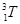 →
→ 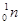 +
+ 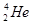 ; г)
; г) 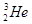 +
+ 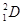 →
→ 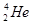 +
+ 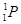 .
.
Пренебрегая кинетической энергией частиц до реакции, определить, какую энергию уносит каждая частица после реакции. Какая из указанных реакций является наиболее оптимальной с практической точки зрения?
2.3. Ядро  , имеющее удельную энергию связи 7,6 МэВ/нуклон, делится на два осколка одинаковой массы, расположенные в середине периодической системы элементов, имеющие удельную энергию связи 8,5 МэВ/нуклон. Определить освободившуюся при этом кинетическую энергию.
, имеющее удельную энергию связи 7,6 МэВ/нуклон, делится на два осколка одинаковой массы, расположенные в середине периодической системы элементов, имеющие удельную энергию связи 8,5 МэВ/нуклон. Определить освободившуюся при этом кинетическую энергию.
3. Учитывая, что в легких ядрах (Z 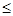 20) число протонов и нейтронов совпадает (А=2Z), а средние и тяжелые ядра перегружены нейтронами, так что зависимость А(Z) при Z > 20 можно интерполировать линейной функцией:
20) число протонов и нейтронов совпадает (А=2Z), а средние и тяжелые ядра перегружены нейтронами, так что зависимость А(Z) при Z > 20 можно интерполировать линейной функцией:
A=KZ+C.
Найти параметры К и С, используя в качестве опорных ядра кальция (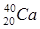 ) и ртути
) и ртути 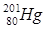 . На основании полученных результатов, и используя данные периодической таблицы Менделеева (Приложение № 2), составить таблицу с указанием параметров Z, AЭ, NЭ, АТ, ∆A и NЭ/Z для ядер с 10
. На основании полученных результатов, и используя данные периодической таблицы Менделеева (Приложение № 2), составить таблицу с указанием параметров Z, AЭ, NЭ, АТ, ∆A и NЭ/Z для ядер с 10 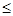 Z
Z 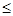 90 и шагом ∆Z=10, где AЭ, NЭ - экспериментальные значения А и N, ∆A = АТ - АЭ.
90 и шагом ∆Z=10, где AЭ, NЭ - экспериментальные значения А и N, ∆A = АТ - АЭ.
Построить график зависимости 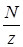 от Z, на котором отметить такие соответствующие экспериментальные значения
от Z, на котором отметить такие соответствующие экспериментальные значения 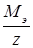 (диаграмма Сегре).
(диаграмма Сегре).
4. Используя экспериментальные данные по дефектам масс атомов (приложение № 1), вычислить полную и удельную энергию связи дважды магических ядер: 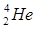 ,
, 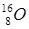 ,
, 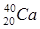 ,
, 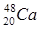 ,
, 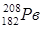 .
.
5. Рассмотреть ряд самых легких ядер: 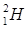 ,
, 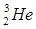 ,
, 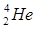 ,
, 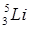 , каждое из которых получается из предыдущего присоединением одного нуклона. Используя данные по дефектам масс соответствующих атомов, приведенные в таблице, оценить энергию присоединения нуклона к предыдущему ядру. Какие выводы можно сделать из сравнения полученных данных?
, каждое из которых получается из предыдущего присоединением одного нуклона. Используя данные по дефектам масс соответствующих атомов, приведенные в таблице, оценить энергию присоединения нуклона к предыдущему ядру. Какие выводы можно сделать из сравнения полученных данных?
Таблица 3. Дефекты масс легчайших атомов.
| Атом | 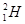
| 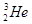
| 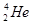
| 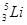
|
| δ(Z,A) | 13,136 | 14,932 | 2,425 | 11,680 |
6. Ядра, перегруженные протонами или нейтронами, являются 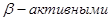 и испытывают
и испытывают 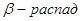 или
или 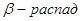 .
.
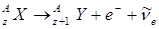 (
(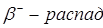 )
)
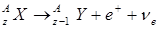 (
(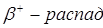 ).
).
Используя формулу Бете-Вайцзеккера, определить заряд Z0 изобарных ядер (А=const), которые являются стабильными относительно 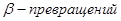 , т.е. обладают максимальной энергией связи для данного А. Для этого необходимо решить уравнение
, т.е. обладают максимальной энергией связи для данного А. Для этого необходимо решить уравнение 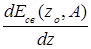 = 0. Определить характер
= 0. Определить характер 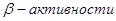 атомных ядер серебра
атомных ядер серебра  , олова
, олова  и цезия
и цезия 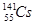 .
.
Контрольные вопросы.
1. В каких единицах измеряется масса атомных ядер в ядерной физике?
2. Дать определения понятия изотопов, изобаров, изотонов и зеркальных ядер.
3. Дать определение энергии связи (удельной энергии связи) ядра. Какую энергию необходимо затратить, чтобы выбить 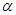 -частицу из ядра
-частицу из ядра 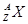 ?
?
4. Что такое дефект массы ядра? Записать формулу для энергии связи ядра через дефекты масс.
5. Записать формулу Бете-Вайцзеккера и пояснить физический смысл каждого слагаемого.
6. Почему выделяется энергия при слияние легких ядер и деление тяжелых.
7. Какие эффекты говорят в пользу жидкокапеельной модели ядра.
8. Получить связь между массой и энергией связи ядра.
Литература.
1. Широков Ю.М., Юдин Н.П. Ядерная физика. М. Наука 1980.
2. Сивухин Д.В. Общий курс физики. Атомная и ядерная физика. Т. 5, часть 2, М. Наука 1989.
Информация для преподавателя.
2.1. Есв = 2∆(2,4) + ∆n - ∆(4,9) = 2×2,42485 + 8,07162 – 11,3484 = 1,5729 МэВ
Т.к. Есв мала, то при облучении 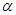 -частицами ядра
-частицами ядра 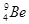 легко выбивается нейтрон.
легко выбивается нейтрон.
2.2. а) Q = 2∆(1,2) - ∆(1,1) - ∆(1,3) = 4,033 МэВ.
Е(р) = 3,025 МэВ; Е(т) = 1,008 МэВ.
б) Q = 3,27 МэВ; E(n) = 2,453 МэВ; E(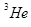 ) = 0,817 МэВ;
) = 0,817 МэВ;
в) Q = 17,59 МэВ; E(n) = 14,07 МэВ; E(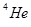 ) = 3,52 МэВ;
) = 3,52 МэВ;
г) Q = 18,35 МэВ; E(р) = 14,68 МэВ; E(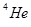 ) = 3,67 МэВ.
) = 3,67 МэВ.
Наиболее оптимальными с энергетической точки зрения являются реакции (в-г). Однако на практике наиболее важной является реакция (в).
2.3. -238 × 7,6 – (-238×8,5) = 214 МэВ.
3. А = КZ + C = 2.6833 × Z - 13.6667
| Z | |||||||||
| AЭ | |||||||||
| NЭ | |||||||||
| АТ | |||||||||
| ∆A | -4 | ||||||||
| NЭ/Z | 1,17 | 1,28 | 1,38 | 1,4 | 1,47 | 1,51 | 1,58 |
4. Есв=[Zδн + Nδn - δ(Z,A) ] (МэВ)
| Ядро | 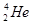
| 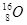
| 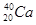
| 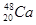
| 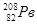
|
| Есв МэВ | 28,297 | 127,625 | 342,066 | 416,018 | 1636,513 |
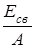 , МэВ/нуклон , МэВ/нуклон
| 7,074 | 7,976 | 8,552 | 8,667 | 7,867 |
5. Есв=Zδн + Nδn - δ(Z,A)
En = Есв(Z,А) - Есв(Z,А-1)
Eр = Есв(Z,А) - Есв(Z-1,А-1)
| Ядро | n | p | 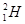
| 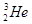
| 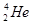
| 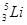
|
| Дефекты массы атома, (МэВ) | 8,072 | 7,289 | 13,136 | 14,932 | 2,425 | 11,680 |
| Есв, (МэВ) | 2,225 | 7,718 | 28,297 | 26,331 | ||
| Энергия присоединения En, Eр, (МэВ) | 2,225 | 5,493 | 20,579 | -1,966 |
Происходит формирование замкнутых оболочек ядра 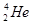 .
.
Ядро 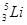 не может быть стабильным, т.к. Eр < 0
не может быть стабильным, т.к. Eр < 0
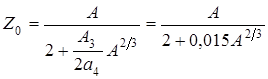
A = 103 => Zo = 45; Z = 47 => 
A = 127 => Zo = 54; Z = 50 => 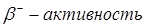
A = 141=> Zo = 60; Z = 55 => 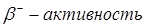
Приложение 1
ТАБЛИЦА СВОЙСТВ ИЗОТОПОВ
|
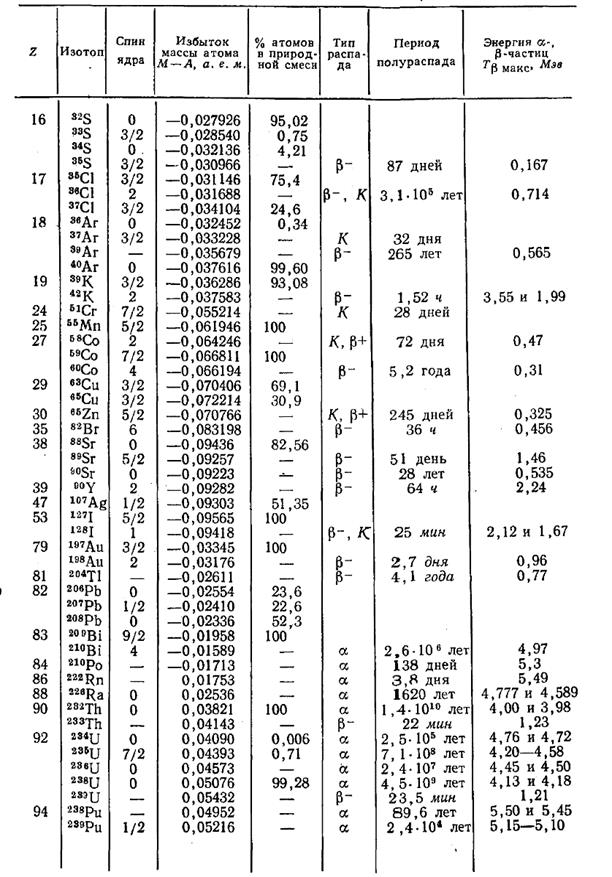
 |
ПЕРИОДИЧЕСКАЯ СИСТЕМА ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
Date: 2015-09-05; view: 730; Нарушение авторских прав