Дифракция Фраунгофера от щели

Описанные в предыдущем разделе построения Френеля позволяют рассчитать 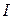позади 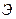с круглым отверстием в точке, лежащей на оси симметрии. Найти вид всей дифракционной картины очень сложно. Однако можно осуществить такие условия наблюдения дифракционного спектра, при которых возможен полный расчет 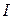на экране. Пусть отверстие в экране представляет собой длинную щель шириной 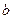, на которую падает плоская волна (рис. 5).

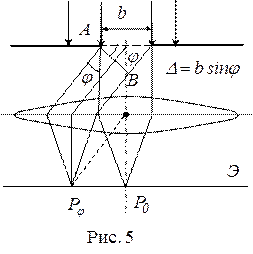Согласно принципу Гюйгенса – Френеля, волновую поверхность падающей волны в плоскости щели следует разбить на столь малые участки, чтобы колебания в точке 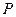, вызываемые вторичными волнами от всех точек одного участка, имели бы почти одинаковую фазу.

Для нахождения результирующей амплитуды колебаний в любой точке экрана 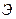необходимо знать распределение фаз всех колебаний, приходящих в эту точку. Так как линза не вносит дополнительной разности хода, то распределение фаз в точке 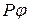будет таким же, как и в плоскости 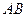, образующей с плоскостью щели угол 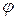. Сумма когерентных

возмущений от всех участков этой поверхности равна

.

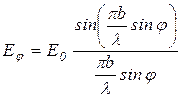Распределение интенсивности света (как величины ~ 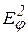) на экране, расположенном в фокальной плоскости линзы, описывается выражением

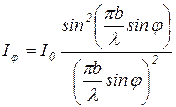, (2.1)

где 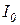– интенсивность света, идущего от всей щели в направлении .

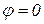При значении углов дифракции 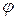, удовлетворяющих условию

,

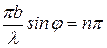т.е. при 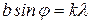( 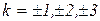– порядок дифракции) 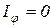. Количество наблюдаемых минимумов 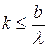, так как .

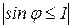Найдем положения максимума – для этого надо продифференцировать выражение (2.1) и приравнять производную нулю. Введем обозначение .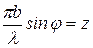

.

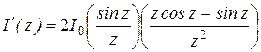Из условия 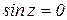определяются положения минимумов; 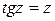– максимумов. Решая трансцендентное уравнение 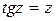графически (рис. 6), получим значения 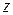, при котором .

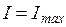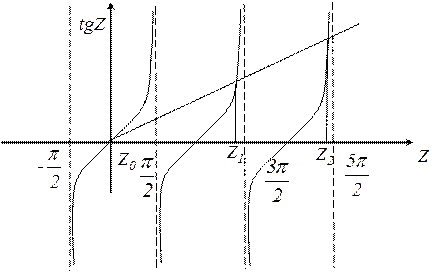Рис. 6

Данное уравнение имеет бесчисленное множество решений, так как имеется бесчисленное множество точек пересечения графиков функци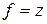и и 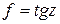, однако число 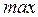не превышает числа .

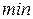Таблица 1

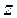
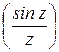
1,43	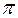0,047
2,46	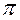0,016
…….	……..

На основании проведенного анализа можно построить график 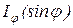(рис. 7). Угловая ширина центрального максимума .

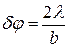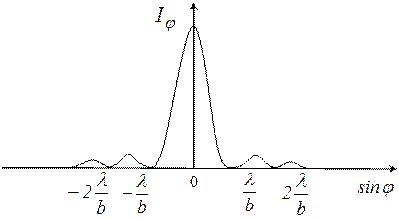На максимум первого порядка приходится 5 % падающей энергии, на максимум второго порядка – 2 %. Отметим, что подобная картина будет наблюдаться, если 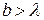, но эти параметры соизмеримы. Ес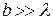ли или 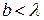, то дифракционная картина не наблюдается.

Рис. 7

Date: 2015-09-05; view: 311; Нарушение авторских прав