
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема о предельных вероятностях
|
|
Методические указания к проведению лекционного занятия
Тема № 9.9. Марковские процессы
План:
1. Основные понятия и определения
2. Теорема о предельных вероятностях
3. Области применения цепей Маркова
4. Управляемые цепи Маркова. Выбор стратегии
Основные понятия и определения
Пусть { 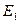 ,
, 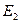 ,...,
,..., 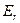 } - множество возможных состояний некоторой физической системы. В любой момент времени система может находиться только в одном состоянии. С течением времени система переходит последовательно из одного состояния в другое. Каждый такой переход называется шагом процесса.
} - множество возможных состояний некоторой физической системы. В любой момент времени система может находиться только в одном состоянии. С течением времени система переходит последовательно из одного состояния в другое. Каждый такой переход называется шагом процесса.
Для описания эволюции этой системы введем последовательность дискретных случайных величин 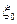 ,
, 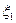 ,...,
,..., 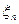 ,... Индекс n играет роль времени. Если в момент времени n система находилась в состоянии
,... Индекс n играет роль времени. Если в момент времени n система находилась в состоянии 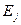 , то мы будем считать, что
, то мы будем считать, что 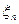 = j. Таким образом, случайные величины являются номерами состояний системы.
= j. Таким образом, случайные величины являются номерами состояний системы.
Последовательность 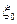 ,
, 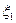 ,...,
,..., 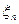 ,... образует цепь Маркова, если для любого n и любых
,... образует цепь Маркова, если для любого n и любых 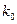 ,
, 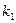 ,...,
,..., 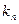 ,...
,...
P(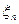 =j /
=j / 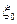 =
= 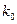 ,...,
,..., 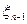 =i)=P(
=i)=P(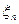 =j /
=j / 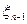 =i).
=i).
Для цепей Маркова вероятность в момент времени n попасть в состояние 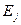 , если известна вся предыдущая история изучаемого процесса, зависит только от того, в каком состоянии находился процесс в момент n-1. То есть при фиксированном "настоящем" "будущее" не зависит от "прошлого". Свойство независимости "будущего" от "прошлого" при фиксированном "настоящем" называется марковским свойством.
, если известна вся предыдущая история изучаемого процесса, зависит только от того, в каком состоянии находился процесс в момент n-1. То есть при фиксированном "настоящем" "будущее" не зависит от "прошлого". Свойство независимости "будущего" от "прошлого" при фиксированном "настоящем" называется марковским свойством.
Вероятности 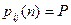 (
(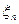 =j /
=j / 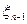 =i), i, j=1,2,..., r называются вероятностями перехода из состояния
=i), i, j=1,2,..., r называются вероятностями перехода из состояния  в состояние
в состояние 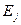 за один шаг.
за один шаг.
Цепь Маркова называется однородной, если вероятности перехода 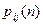 не зависят от n, т.е. если вероятности перехода не зависят от номера шага, а зависят только от того, из какого состояния и в какое осуществляется переход. Для однородных цепей Маркова вместо
не зависят от n, т.е. если вероятности перехода не зависят от номера шага, а зависят только от того, из какого состояния и в какое осуществляется переход. Для однородных цепей Маркова вместо 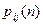 будем писать
будем писать 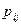 .
.
Вероятности перехода удобно располагать в виде квадратной матрицы
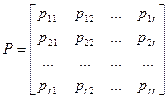
Матрица P называется матрицей вероятностей перехода однородной цепи Маркова за один шаг. Она обладает следующими свойствами:
а) 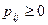 ;
;
б) для всех i: 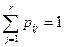
Квадратные матрицы, для которых выполняются условия а) и б), называются стохастическими.
Вектор 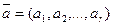 , где
, где  =P(
=P(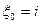 ), i=1,2...,r называется вектором начальных вероятностей.
), i=1,2...,r называется вектором начальных вероятностей.
Свойства однородных цепей Маркова полностью определяются вектором начальных вероятностей и матрицей вероятностей перехода.
Приведем пример: Завод выпускает телевизоры определенного типа. В зависимости от того, находит ли данный тип телевизора спрос у населения, завод в конце каждого года может находиться в одном из состояний: состояние 1 – спрос есть, состояние 2 – спроса нет. Пусть вероятность сохранить состояние 1 в в следующем году с учетом возможного изменения спроса равна 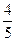 , а вероятность изменить состояние 2 с учетом мероприятий по улучшению выпускаемой модели равна
, а вероятность изменить состояние 2 с учетом мероприятий по улучшению выпускаемой модели равна 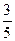 . Тогда процесс производства на данном заводе можно описать цепью Маркова с матрицей переходов:
. Тогда процесс производства на данном заводе можно описать цепью Маркова с матрицей переходов:
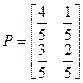
В конкретных случаях для описания эволюции цепи Маркова вместо явного выписывания матрицы P используют граф, вершинами которого являются состояния цепи, а стрелка, идущая из состояния  в состояние
в состояние 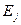 с числом
с числом 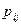 над ней показывает, что из состояния
над ней показывает, что из состояния  в состояние
в состояние 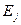 возможен переход с вероятностью
возможен переход с вероятностью 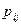 . В том случае, когда
. В том случае, когда 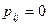 , соответствующая стрелка не проводится.
, соответствующая стрелка не проводится.
Можно показать, что матрица вероятностей перехода цепи Маркова за n шагов равняется n-ой степени матрицы P вероятностей перехода за один шаг. Для однородной цепи Маркова при любом m выполняется равенство
P( )=P(
)=P(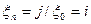 ).
).
Но последняя вероятность есть вероятность перехода из состояния  в состояние
в состояние 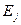 за n шагов.
за n шагов.
Теорема о предельных вероятностях
В 1930 году Дж.Биркгофом и Дж.фон Нейманом была сформулирована и доказана одна из основных эргодических теорем – теорема о предельных вероятностях:
Если при некотором 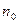 все элементы матрицы
все элементы матрицы 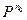 =[
=[ 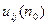 ] положительны, то существуют пределы
] положительны, то существуют пределы

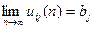 , i,j =1,2,...,r.
, i,j =1,2,...,r.
Предельные вероятности  не зависят от начального состояния
не зависят от начального состояния  и являются единственным решением системы уравнений
и являются единственным решением системы уравнений
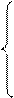
|
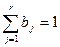 ,
,
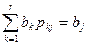 , j=1, 2,..., r.
, j=1, 2,..., r.
Физический смысл этой теоремы заключается в том, что вероятности нахождения системы в состоянии 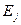 практически не зависят от того, в каком состоянии она находилась в далеком прошлом.
практически не зависят от того, в каком состоянии она находилась в далеком прошлом.
Цепь Маркова, для которой существуют пределы  , называется эргодической. Решение (
, называется эргодической. Решение (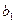 ,
, 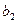 ,...,
,..., 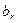 ) написанной выше системы (1) называется стационарным распределением вероятностей для марковской цепи с матрицей перехода P = [
) написанной выше системы (1) называется стационарным распределением вероятностей для марковской цепи с матрицей перехода P = [ 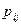 ].
].
Если из состояния  система может перейти в состояние
система может перейти в состояние 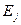 с положительной вероятностью за конечное число шагов, то говорят, что
с положительной вероятностью за конечное число шагов, то говорят, что 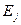 достижимо из
достижимо из  .
.
Состояние  называется существенным, если для каждого состояния
называется существенным, если для каждого состояния 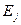 , достижимого из
, достижимого из  ,
,  достижимо из
достижимо из 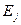 . Если же для хотя бы одного j
. Если же для хотя бы одного j 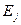 достижимо из
достижимо из  , а
, а  не достижимо из
не достижимо из 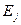 , то
, то  - несущественное состояние.
- несущественное состояние.
Date: 2015-09-20; view: 1267; Нарушение авторских прав