Деревья и циклы

Определение. Граф G называется деревом, если он является связным и не имеет циклов. Граф G, все компоненты связности которого являются деревьями, называется лесом.

У графа, который является деревом, число ребер на единицу меньше числа вершин. Дерево не содержит циклов, любые две его вершины можно соеденить единственной простой цепью.

Если у дерева G есть, по крайней мере, одно ребро, то у него обязательно найдется висячая вершина, т.к. в противном случае в графе будет цикл.

Для графов, которые сами по себе не являются деревьями, вводится понятие остовного дерева.

Определение. Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

Пусть G – связный граф. Тогда остовное дерево графа G (если оно существует) должно содержать n(G)-1 ребер.

Таким образом, любое остовное дерево графа G есть результат удаления из графа G ровно m(G) - (n(G) - 1) = m(G) – n(G) + 1 ребер.

Число v (G) = m(G) – n(G) + 1 называется цикломатическим числом связного графа G.

Одной из самых распространенных задач является задача построения остовного дерева минимальной длины графа. Для решения этой задачи применяется следующий алгоритм.

1) Выберем в графе G ребро минимальной длины. Вместе с инциндентными ему вершинами оно образует подграф G₂.

2) Строим граф G₃, добавляя к графу G₂ новое ребро минимальной длины, выбранное среди ребер графа G, каждое из которых инциндентно какой либо вершине графа G₂, и одновременно инциндентно какой – либо вершине графа G, не содержащейся в графе G₂.

3) Строим графы G₄, G₅, …, G_n, повторяя действия пункта 2 до тех пор, пока не переберем все вершины графа G.

Пример. Определить минимальное остовное дерево нагруженного графа.

Граф называется нагруженным, если на множестве его дуг задана некоторая функция, которая называется весовой функцией, и определяет длину дуги.

В нашем примере – весовая функция определяет длины дуг числами 1, 2, 3, 4, 5.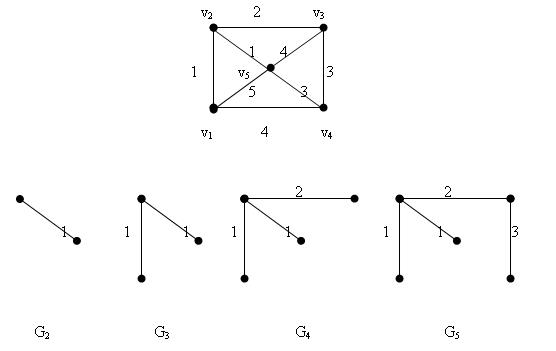

На четвертом шаге алгоритма получили дерево G₅, которое соединяет все вершины исходного графа. Таким образом, дерево G₅, будет минимальным остовным деревом графа G.

Контрольные вопросы:

1. Что называется графом, псевдографом, мультиграфом, орграфом?

2. Что называется маршрутом (путем) для графа G(V, X)?

3. Как составляются матрицы смежности и инцидентности?

4. Какой граф называется связным, эйлеровым, гамильтоновым, деревом?

Литература:

1. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2005. – 471 с.

2. Общий курс высшей математики для экономистов: Учебник. / Под ред. В.И. Ермакова. –М.: ИНФРА-М, 2006. – 655 с.

3. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред.В.И. Ермакова. М.: ИНФРА-М, 2006. – 574 с.

4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2. – М.: Оникс 21 век: Мир и образование, 2005. – 304 с. Ч. 1; – 416 с. Ч. 2.

5. Математика в экономике: Учебник: В 2-х ч. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандара. – М.: Финансы и статистика, 2006.

6. Шипачев В.С. Высшая математика: Учебник для студ. вузов – М.: Высшая школа, 2007. – 479 с.

Date: 2015-09-20; view: 547; Нарушение авторских прав