Если в ходе решения любой задачи у вас получилось какое-то другое значение вероятности – ищите ошибку

При классическом подходе к определению вероятности крайние значения (ноль и единица) получаются посредством точно таких же рассуждений. Пусть из некой урны, в которой находятся 10 красных шаров, наугад извлекается 1 шар. Рассмотрим следующие события:

К – из урны будет извлечён красный шар;

М – из урны будет извлечён зелёный шар.

Общее количество исходов: n = 10. Событию K благоприятствуют все возможные исходы m = 10, следовательно, 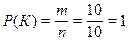, то есть данное событие достоверно. Для второго события благоприятствующие исходы отсутствуют (в урне нет зеленых шаров) и поэтому m = 0. Следовательно, 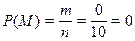, то есть событие М невозможно.

Особый интерес представляют события, вероятность наступления которых чрезвычайно мала. Хоть такие события и являются случайными, для них справедлив следующий постулат:

в единичном испытании маловозможное событие не произойдёт.

Именно поэтому Вы не сорвёте в лотерее Джек-пот, если вероятность этого события, скажем, равна 0,00000001. Да-да, именно Вы – с единственным билетом в каком-то конкретном тираже. Впрочем, б о льшее количество билетов и б о льшее количество розыгрышей Вам особо не помогут....Когда я рассказываю об этом окружающим, то почти всегда в ответ слышу: «но ведь кто-то выигрывает». Хорошо, тогда давайте проведём следующий эксперимент: пожалуйста, сегодня или завтра купите билет любой лотереи (не откладывайте!). И если выиграете... ну, хотя бы больше 50-ти килорублей, обязательно отпишитесь – я объясню, почему это произошло. За процент, разумеется.

Но грустить не нужно, потому что есть противоположный принцип: если вероятность некоторого события очень близка к единице, то в отдельно взятом испытании оно практически достоверно произойдёт. Поэтому перед прыжком с парашютом не надо бояться, наоборот – улыбайтесь! Ведь должны сложиться совершенно немыслимые и фантастические обстоятельства, чтобы отказали оба парашюта.

Хотя всё это лирика, поскольку в зависимости от содержания события первый принцип может оказаться весёлым, а второй – грустным; или вообще оба параллельными.

Пожалуй, пока достаточно, на уроке Задачи на классическое определение вероятности мы выжмем максимум из формулы 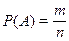. В заключительной же части этой статьи рассмотрим одну важную теорему:

Сумма вероятностей событий, которые образуют полную группу, равна единице. Грубо говоря, если события образуют полную группу, то со 100%-й вероятностью какое-то из них произойдёт. В самом простом случае полную группу образуют противоположные события, например:

– в результате броска монеты выпадет орёл;
– в результате броска монеты выпадет решка.

По теореме: Р(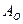) + Р() = 1, так как данные события равновозможны и их вероятности одинаковы .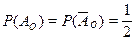

По причине равенства вероятностей равновозможные события часто называют равновероятными.

Пример с кубиком:

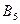– в результате броска игрального кубика выпадет 5 очков;
– в результате броска игрального кубика выпадет число очков, отличное от пяти.

События 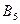и противоположны, они образуют полную группу событий, поэтому .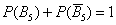

Рассматриваемая теорема удобна тем, что позволяет быстро найти вероятность противоположного события. Так, если известна вероятность 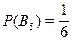того, что выпадет пятёрка, легко вычислить вероятность того, что она не выпадет:

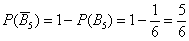
Это гораздо проще, чем суммировать вероятности пяти элементарных исходов. Для элементарных исходов, к слову, данная теорема тоже справедлива: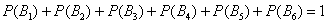

События , , 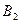, , 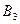, , 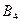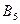как отмечалось выше, равновозможны – и теперь мы можем сказать, что равновероятны. Вероятность выпадения любой грани кубика равна :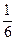

Ну и на закуску колода: поскольку нам известна вероятность 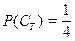того, что будет извлечена трефа, то легко найти вероятность того, что будет извлечена карта другой масти:

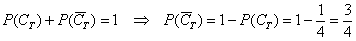
Заметьте, что рассмотренные пары событий , и С_Т, 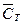не равновероятны, как оно чаще всего и бывает.

В упрощенной версии записи решения вероятность противоположного события стандартно обозначается строчной буквой q. Например, если p = 0,7 – вероятность того, что стрелок попадёт в цель, то q = 1 – p = 1 – 0,7 = 0,3 – вероятность того, что он промахнётся.

! В теории вероятностей буквы p и q нежелательно использовать в каких-то других целях.

В завершение урока очень важно, чтобы вы могли ответить на следующие вопросы:

Какие виды событий существуют? – Что такое случайность и равновозможность события? – Как вы понимаете термины совместность/несовместность событий? – Что такое полная группа событий, противоположные события? – Что означает сложение и умножение событий? – В чём суть классического определения вероятности? – Чем полезна теорема сложения вероятностей событий, образующих полную группу?

Нет, зубрить ничего не надо, это всего лишь азы теории вероятностей – своеобразный букварь, который довольно быстро уложится в голове. И чтобы это произошло как можно скорее, предлагаю ознакомиться с уроками Задачи по комбинаторике и Задачи на классическое определение вероятности.

Date: 2015-09-20; view: 493; Нарушение авторских прав