О недифференцируемой оптимизации

Недифференцируемая оптимизация – это обширная область современной теории экстремальных задач и вычислительной математики. Обсудим возможные подходы к исследованию и ре-

шению негладких экстремальных задач на примере минимизации выпуклых недифференцируемых функций.

Пусть выпуклая функция 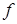определена на и не является всюду дифференцируемой. Несмотря на то, что в любой точке пространства существует производная выпуклой функции 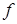по любому направлениям, в точках недифференцируемости градиент не существует. Поэтому определены различные обобщения этого понятия, которые для некоторых целей могут быть «заменителем» градиента. В частности, этим целям служат понятия субградиента и субдифференциала.

Определение 1. Вектор называется субградиентом функции f в точке 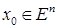, если выполняется неравенство

.

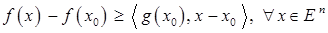Множество 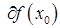субградиентов называется субдифференциалом функции f в точке .

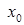В любой точке 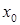субдифференциал выпуклой функции 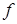– непустое выпуклое замкнутое и ограниченное множество. Если функция 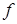дифференцируема в точке 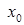, то субградиентом является единственный вектор 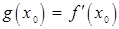. Субградиенты используются, в частности, для изучения экстремальных свойств выпуклых функ-

ций. В терминах субдифференциалов получены общие необходимые и достаточные условия экстремума. На основе субградиентов построены методы минимизации, обобщающие градиентные методы.

Важной и непростой задачей является вычисление субдифференциала или отдельно взятых субградиентов. Нет простых процедур, позволяющих вычислять субдифференциалы в общем случае. Однако для некоторых классов выпуклых функций построить 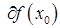и найти какой-либо субградиент 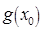не представляет особой сложности.

В качестве примера рассмотрим функцию максимума 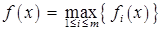. Предположим, что все функции 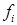– выпуклые и дифференцируемые. Обозначим через

.

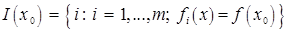Тогда .

В терминах субградиентов необходимое и достаточное условие безусловного минимума выпуклой функции 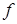в точке 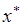имеет вид следующего включения:

.

Познакомимся далее вкратце с субградиентным методом безусловной минимизации или,

как его еще называют, с методом обобщенного градиентного спуска.

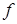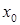Пусть – определенная на выпуклая функция, – произвольный вектор. Начиная с вектора 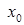, последовательность приближений строится по правилу

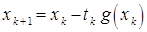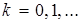, (1)

где 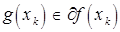, , 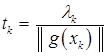числовая последовательность 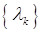, , 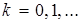такова, что 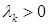, 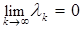и ряд 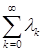расходится.

Заметим, что последовательность 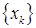, генерируемая субградиентным методом, вообще го-воря, не является релаксационной. При некоторых дополнительных предположениях о функции 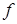последовательность 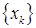– минимизирующая. Последовательность 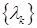может находиться по различным правилам. Например, 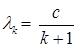, где с – произвольная положительная константа.

Метод прост в реализации (если, конечно, просто вычисляются субградиенты), однако скорость сходимости и достигаемая точность решения существенно зависят от многих факторов и поэтому успешное применение метода не всегда возможно.

Субградиентный метод легко обобщается и для решения условно экстремальных задач. Пусть требуется минимизировать выпуклую функцию 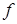на множеств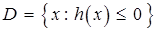е , где 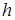– выпуклая на функция.

Так же, как в только что приведенном методе, последовательность приближений строится, начиная с произвольного вектора 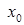, по формуле (1) с той лишь разницей, что вектор 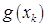является субградиентом функции 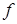, то есть 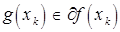, если 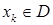, и субградиентом функции 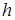, то есть 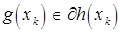, если .

Date: 2015-09-19; view: 977; Нарушение авторских прав