
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача №2. Определение состава удобрений
|
|
Лабораторная работа №1. Решение задач оптимизации с помощью надстройки Поиск решения.
Задача №1. Планирование производства материалов.
Фирма выпускает два типа строительных материалов А и В. Продукция обоих видов поступает в продажу. Для производства материалов используется два исходных продукта: I и II. Максимально возможные суточные запасы этих продуктов составляют 7 и 9 тонн соответсвенно. Расходы продуктов I и II на тонну соответсвующих материалов приведены в таблице:
| Исходный продукт | Расход исходных продуктов, т (на одну тонну материалов) | Максимально возможный запас, т | |
| материал А | материал В | ||
| I | |||
| II |
Изучение рынка сбыта показало, что суточный спрос на материал В никогда не превышает спроса на материал А более чем на 1 т. Кроме того, спрос на материал А никогда не превышает 3т в сутки. Оптовые цены одной тонны материалов равны: 4000 у.е. для В и 3000 у.е. для А. Какое количество материала каждого вида должна производить фабрика, чтобы доход от реализации был максимальным?
Решение:
1. Формулировка математической модели задачи:
· переменные для решения задачи: х1 – суточный объем производства материала А, х2 - суточный объем производства материала В;
· определение функции цели (критерия оптимизации). Суммарная суточная прибыль от производства х1 материала А и х2 материала В равна:
F=4000 х2 +3000 х1
поэтому цель фабрики – среди всех допустимых значений х2 и х1 найти такие, которые максимизируют суммарную прибыль от производства материалов F:
F=4000 х2 +3000 х1 →max;
· ограничения на переменные:
¾ объем производства красок не может быть отрицательным, т.е.
х2 ≥0, х1 ≥0;
¾ расход исходного продукта для производства обоих видов материалов не может превосходить максимально возможного запаса данного исходного продукта, т.е.
2 х2 +3 х1 ≤7
3 х2 +2 х1 ≤9
¾ ограничение на величину спроса на материалы:
х1 - х2 ≤1
х1 ≤3
Таким образом, получаем следующую математическую модель задачи:
· Найти максимум следующей функции:
F=4000 х2+ 3000 х1 →max
· при ограничениях вида:
2 х2 +3 х1 ≤7
3 х2 +2 х1 ≤9
х1 - х2 ≤1
х1 ≤3
х2 ≥0, х1 ≥0;
2. Подготовка листа рабочей книги MS Excel для вычислений – на рабочий лист вводим необходимый текст, данные и формулы как показано на рисунке 1.

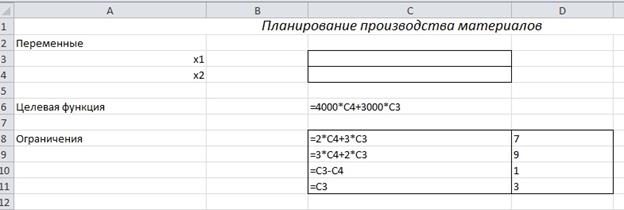 Переменные задачи х1 и х2 находятся соответственно в ячейках С3 и С4. Целевая функция находится в ячейке С6 и содержит формулу =4000*C4+3000*C3.
Переменные задачи х1 и х2 находятся соответственно в ячейках С3 и С4. Целевая функция находится в ячейке С6 и содержит формулу =4000*C4+3000*C3.
Ограничения на задачу учтены в ячейках C8: D11.
3. Работа с надстройкой Поиск решения. На вкладке Данные в группе Анализ щелкните Поиск решения.
Если команда Поиск решения или группа Анализ отсутствует, необходимо загрузить надстройку " Поиск решения " (надстройка - вспомогательная программа, служащая для добавления в Microsoft Office специальных команд или возможностей).
Загрузка надстройки "Поиск решения"
1. На вкладке Файл выберите команду Параметры, а затем — категорию Надстройки.
2. В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти.
3. В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.
Вводим необходимые данные для рассматриваемой задачи:
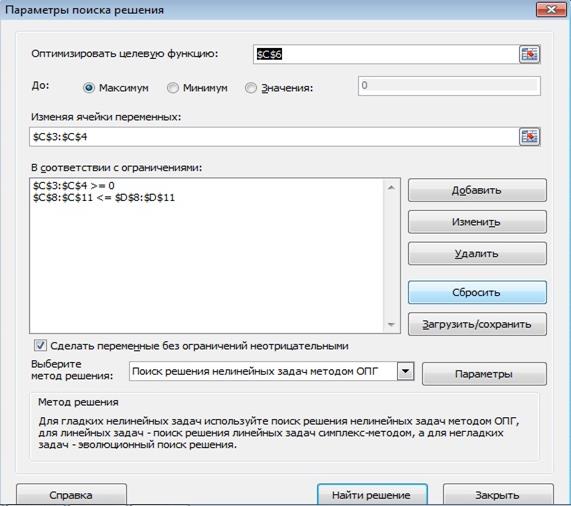
Рисунок 2. Установка необходимых параметров
задачи планирования материалов в окне Поиск решения
Для того чтобы ввести ограничения, необходимо щелкнуть кнопку Добавить. Заполните окно Добавление ограничения, как показано на рисунке:
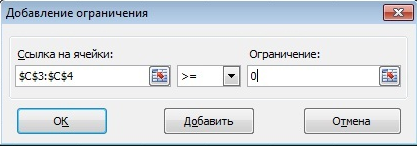
Рисунок 3
Затем щелкните ОК.
Еще раз щелкните Добавить. Вновь заполните окно Добавление ограничения, как показано на рисунке:
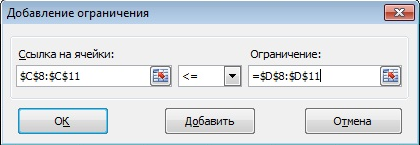
Рисунок 4.
Результат работы по поиску решения представлен на рисунке:
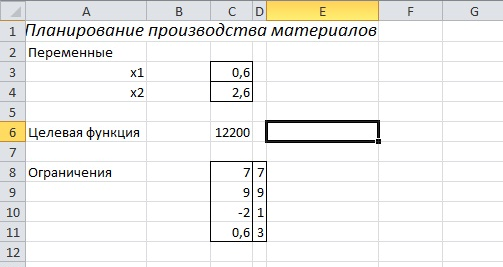
Рисунок 5. Результат расчета надстройки Поиск решения.
Задача №2. Определение состава удобрений.
Для получения удобрений видов 1 и 2 используются химические вещества A, B, C, и D, требования к содержанию которых в удобрениях приведены в таблице:
| Вид удобрения | Требования к содержанию химических веществ |
| Не более 70% вещества А Не более 40% вещества В | |
| От 30 до 50% вещества В Не менее 25% вещества С Не более 65% вещества D |
Характеристики и запасы минералов, используемых для производства химических веществ A, B, C и D, указаны в таблице:
| Минерал | Максимальный запас, т | Состав, % | Цена, у.е./т | |||
| A | B | C | D | |||
Цена 1 т удобрения вида 1 равна 320 у.е., цена 1т удобрения вида 2 – 350 у.е. Необходимо максимизировать прибыль от продажи удобрений видов 1 и 2.
Решение:
1. Математическая модель задачи.
Пусть:
· x A1, x B1, x C1, x D1 – количество химических веществ A, B, C и D, используемых для получения удобрения вида 1;
· x A2, x B2, x C2, x D2 - – количество химических веществ A, B, C и D, используемых для получения удобрения вида 1;
· yi, i = 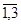 - количество используемого i -го минерала.
- количество используемого i -го минерала.
Найти максимум функции:
F=320(x A1,+ x B1,+ x C1,+ x D1)+350(x A2,+ x B2, + x C2 ,+ x D2)-40y1-50y2-60y3→max
При следующих ограничениях:
· на состав вида удобрения:
x A1≤0,7(x A1,+ x B1,+ x C1,+ x D1),
x B1≤0,4(x A1,+ x B1,+ x C1,+ x D1),
x B2≤0,5(x A2,+ x B2, + x C2 ,+ x D2),
x B2≥0,3(x A2,+ x B2, + x C2 ,+ x D2),
x C2≥0,25(x A2,+ x B2, + x C2 ,+ x D2),
x D2≤0,65(x A2,+ x B2, + x C2 ,+ x D2).
· на характеристики и состав минералов
xA1+ x A2≤0,3y1+0,2y2+0,15y3
x B1+ x B2≤0,2y1+0,3y2+0,15y3
x C1+ x C2≤0,15y1+0,1y2+0,4y3
x D1+ x D2≤0,35y1+0,4y2+0,3y3
· на диапазоны переменных
xi1 ≥0, xi,2 ≥0, i= 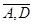
0≤y1≤1200
0≤y2≤2500
0≤y3≤3100
0≤y1≤1200
2. Подготовка листа рабочей книги MS Excel – разместим данные для решения задачи на рабочем листе в соответствии с рисунком:
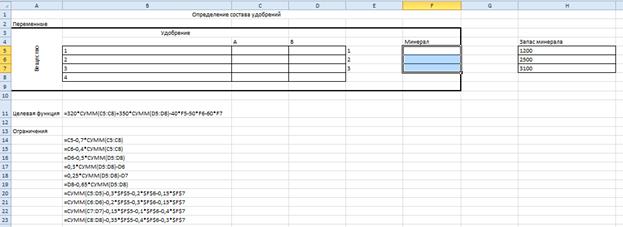
Рисунок 6
3. Ввод данных в окно Поиск решения осуществим в соответствии с рисунком.
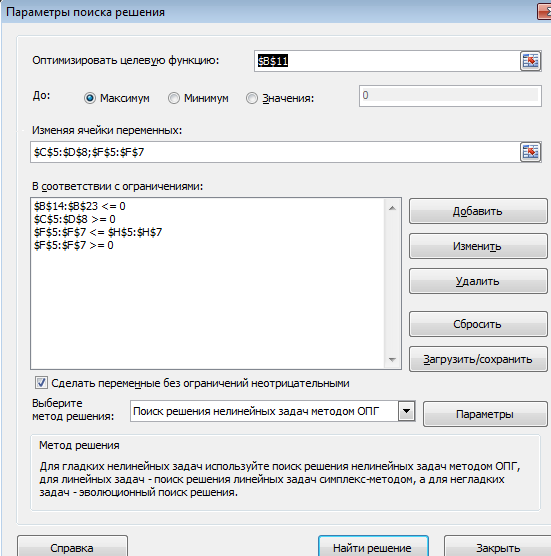
Рисунок 7
Результаты поиска решения, т.е. решение задачи об определении состава удобрений представлены на рисунке:
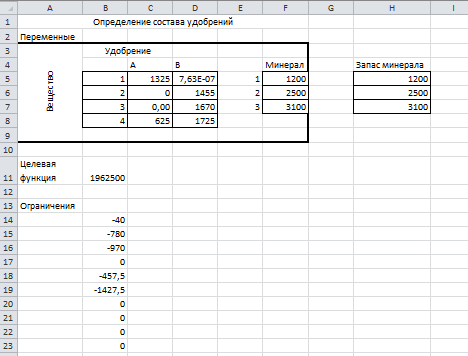
Рисунок 8
| <== предыдущая | | | следующая ==> |
| | | Холодний Яр |
Date: 2015-09-19; view: 1250; Нарушение авторских прав