
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Розрахунок розмірних ланцюгів теоретико-імовірносним методом
|
|
При рішенні прямої задачі методом повної взаємозамінності можуть бути отримані занадто малі величини допусків складових розмірів, що є економічно недоцільним, а іноді просто нездійсненним. Такі високі вимоги до точності отримують тому, що в основу розрахунку покладене припущення про найнесприятливіше сполучення розмірів з'єднуваних деталей. Усі складові ланки не тільки одночасно приймають екстремальні значення, але в одному складальному вузлі всі розміри, що збільшують, розглядаються максимальними, а ті, що зменшують, - мінімальними (чи навпаки). Такий випадок може бути, але імовірність його появи, як показує розрахунок, дуже малий.
Тому в багатьох випадках метод мінімуму-максимуму (так іноді називають метод повної взаємозамінності) розглядається як економічно недоцільна, необгрунтована перестраховка, а розмірні ланцюги розраховують методами неповної взаємозамінності (наприклад, ймовірносним методом). Він грунтується на тому, що розміри, що складають розмірний ланцюг, розглядаються як незалежні перемінні випадкові величини, а ланка, що замикає, - як сума незалежних перемінних. Розглядаються закони розсіювання значень розмірів, які складають розмірний ланцюг, і випадковий характер їхнього з'єднання при складальній операції.
Встановлено, що картина, розсіювання розмірів деталей яка спостерігається на практиці, при різних методах їх обробки може бути описана відомими в теорії ймовірностей законами рівної імовірності, рівнобедреного трикутника (закон Сімпсона) та ін., але найчастіше - законом нормального розподілу (законом Гауса).
При прийнятті деяких технологічно обгрунтованих допущень допуск ланки, що замикає, визначається з виразу
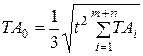 (9.9)
(9.9)
Тут t - безрозмірний коефіцієнт, обумовлений так званим відсотком ризику р. Під відсотком ризику розуміють відсоток вузлів або виробів, у яких в результаті складання дійсне значення ланки, що замикає, виходить за припустимі межі. Це іноді відбувається в тих випадках, коли дійсні значення складових розмірного ланцюга розмірів дорівнюють гранично припустимим чи близькі до них, а сполучення розмірів найбільш несприятливе. Таке може статися, наприклад, коли всі розміри, що збільшують, у даному вузлі мають найменші значення в межах допуску, а ті, що зменьшують, в цьому ж вузлі - максимальні значення. Отриманий при складанні брак можна виправити. Для цього досить розібрати вузол і замінити кілька деталей, щоб з'єднання дійсних розмірів стало більш сприятливим. Витрати на розбирання деякої кількості вузлів багаторазово перекриваються економічним ефектом від зниження вимог до точності розмірів, що входять у розмірний ланцюг. Розрахунок розмірних ланцюгів на основі теорії ймовірностей широко застосовується в промисловості.
Значення коефіцієнта t по заданому конструктором відсотку ризику р беруть з табл. 9.6.
Таблиця 9.6 - Значення коефіцієнту t при різних процентах ризику p
| р,% | 0,01 | 0,05 | 0,1 | 0,2 | 0,27 | 0,4 | 0,5 | 0,6 | 0,7 |
| t | 3,89 | 3,48 | 3,29 | 3,12 | 3,00 | 2,88 | 2,81 | 2,75 | 2,70 |
| р,% | 0,8 | 0,9 | 1,0 | 1,5 | 2,0 | 3,0 | 5,0 | 10,0 | 32,0 |
| t | 2,65 | 2,61 | 2,57 | 2,43 | 2,33 | 2,17 | 1,96 | 1,65 | 1,00 |
Під час вирішення прямої задачі є заданими номінальні розміри всіх складових ланок, а також граничні розміри вихідної ланки. Потрібно визначити граничні відхилення складових ланок, враховуючи ймовірносний закон.
Задачу найчастіше вирішують також способом рівної точності, припускаючи, що всі складові розміри будуть виконуватися по одному квалітету. Спосіб виключає необгрунтоване завищення точності виконання деяких розмірів і технологічні труднощі, які випливають з цього. У виразах допуску складових ланок через одиницю допуску: (це було вже зроблено вище) приймаємо, що a 1 =а 2 =... = а. Тоді формула (9.9) прийме вид (за відсутності стандартних, покупних деталей з фіксованою величиною допуска):
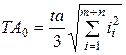 i
i 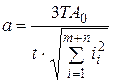 (9.10)
(9.10)
Значення одиниць допуску для різних інтервалів беруться з табл. 9.2. Звичайно отримане значення а знаходиться між двома стандартними значеннями, що визначають квалітети (див. табл. 9.3). У цих випадках доцільно допуск частини складових ланок призначати по точнішому квалітету, а допуск інших - по грубішому. Допуск однієї ланки, так званої ув'язочної, приймають не стандартним, так, щоб рівняння (9.9) виконувалося.
З формули (9.9) допуск ув'язочної ланки
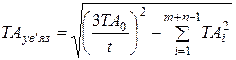 (9.11)
(9.11)
Граничні відхилення ув'язочної ланки шукають на підставі теореми про математичні очікування. Відомо, що математичне очікування суми випадкових величин дорівнює сумі математичних очікувань цих величин. Вважаючи, що діапазон розсіювання розміру дорівнює його допуску, а математичне очікування розміру збігається із серединою поля допуску, можна записати-
 (9.12)
(9.12)
Для полегшення розрахунку вводять поняття про середнє відхилення розміру
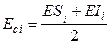 . (9.13)
. (9.13)
Тоді
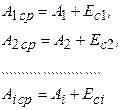 (9.14)
(9.14)
Після підстановки в (9.12) і перетворення остаточно одержуємо
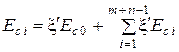 . (9.15)
. (9.15)
Тут коефіцієнт ξ'=+1 для ланок, напрямок яких протилежний напрямку ув'язочної ланки; ξ'=-1 для ланок, напрямок яких збігається з напрямком ув'язочної ланки.
Граничні відхилення ув'язочної ланки знаходять по формулах

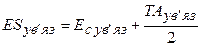 ; (9.16)
; (9.16)
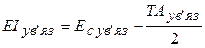 . (9.17)
. (9.17)
Допуски на розміри складових ланок звичайно призначають "у тіло", як і при розрахунку методом повної взаємозамінності.
Розрахунок прямої задачі методом неповної взаємозамінності рекомендується виконувати в наступній послідовності:
1) визначити номінальний розмір вихідної ланки;
2) визначити середнє число одиниць допуску;
3) призначити ув'язочну ланку;
4) вибрати квалітети і призначити допуски на усі ланки, крім ув'язочної;
5) визначити допуск ув'язочної ланки;
6) визначити середнє і граничні відхилення ув'язочної ланки. Результати розрахунку зводяться в табл. 9.7.
Таблиця 9.7 - Таблиця для розрахунку теоретико-імовірносним методом
| Позначен- ня розміру (ланки) | Номіналь- ний розмір ланки, мм | Одиниця допуску i, мкм | Ква- лі- тет | Допуск розміру ТАі, м км | Відхилення розмірів, мм | Умовне позначення полів допусків | ||
| Верхнє ЕSi | Нижнє ЕIi | Середнє Еc i | ||||||
Щоб отримати уяву про доцільність використання цього методу в якості прикладу залишимо ті ж самі вихідні дані, що і в першому випадку.
Вирішимо пряму задачу для складальної одиниці, представленої на рис. 9.1, а. Умови задачі залишимо такими ж, як і при розрахунку методом повної взаємозамінності.
Дано: A 1 =10 мм, А 2 =20 мм, А 3 =81 мм, А 4 =10 мм, А 5 =80 мм.
A 0 max = 1,400 мм, A 0 min = 0,900 мм, р = 0,55%.
Знайти граничні відхилення складових ланок.
1) Знаходимо номінальний розмір замикаючої ланки. Зі схеми розмірного ланцюга (див. рис. 9.1, б) маємо
А 0= (А 2 + А 3)-(А 1+ А 4 + А 5)= (20 + 81)-(10 +10 + 80)=1 мм.
Тоді 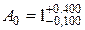 i
i 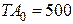 мкм.
мкм.
2) Визначаємо по формулі (9.10) середнє число одиниць допуску. По заданому відсотку ризику з табл. 9.6 за допомогою інтерполяції знаходимо, що t= 2,78. (Стандартні, покупні деталі - відсутні в складальній одиниці).
Тоді
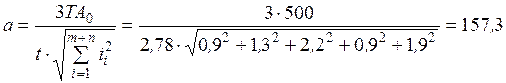 .
.
Знайдене значення (див. табл. 9.3) розташовується між 11 (а= 100) і 12 (а= 160) квалітетами. Але набагато ближче до 12 квалітету.
3)За ув'язочний розмір приймаємо А 2.
4)Розмір А 5 виконуємо по 11 квалітету, а всі інші складові ланки - по 12. Допуски розмірів призначаємо "у тіло".
5)Визначаємо по формулі (9.11) допуск ув'язочної ланки
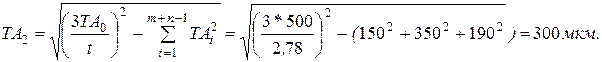
По табл. 9.4 встановлюємо, що отримана величина допуску знаходиться між 12 і 13 квалітетами. З технологічної точки зору це є досить сприйнятним.
6) Визначаємо по формулі (9.15) середнє відхилення ув'язочної ланки. Враховуємо, що для нашого випадку ξ' = -1 для ланки А 3, для всіх інших ланок ξ’ = +1.
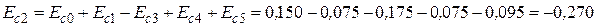 .
.
Тоді
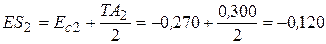 мм,
мм,
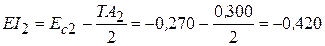 мм.
мм.
Отже, ув'язочна ланка 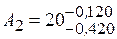 .
.
Приведений приклад показує, що розрахунок методом неповної взаємозамінності дозволяє значно розширити допуски складових ланок у порівнянні з методом повної взаємозамінності (в середньому на 2 квалітети). Замість 10 квалітету можна виконувати розміри деталей за 12 квалітетом. Це робить виробництво більш дешевим. При цьому процент можливого браку буде дорівнювати 0,55%. Таким чином буде проводитися розкладання й нове складання приблизно 1 складальної одиниці з 200, що майже не вплине на збільшення робочого часу.
Результати розрахунку зведені в табл. 9.8.
Таблиця 9.8 - Розрахунок розмірного ланцюга теоретико-імовірносним методом
| Позначення розміру (ланки) | Номінальний розмір ланки, мм | Одиниця допуску i, мкм | Квалiтет | Допуск розміру ТАі, мкм | Відхилення розмірів, мм | Умовне позначення полів допусків | ||
| Верхнє ЕSi | Нижнє ЕIi | Середнє Еci | ||||||
| А 1 | 0,90 | -0,150 | -0,075 | h 12 | ||||
| А 2 | 1,30 | - | -0,120 | -0,420 | -0,270 | - | ||
| А 3 | 2,20 | +0,350 | +0,175 | Н 12 | ||||
| А 4 | 0,90 | -0,150 | -0,075 | h 12 | ||||
| А 5 | 1,90 | -0,190 | -0,095 | h 11 | ||||
| А 0 | - | - | +0,400 | -0,100 | +0,150 | - |
Date: 2015-09-18; view: 438; Нарушение авторских прав