Введение. Методы оптимизации, как научная дисциплина, по существу считается частью более общей дисциплины – «Исследование операций»

Методы оптимизации, как научная дисциплина, по существу считается частью более общей дисциплины – «Исследование операций». Начало ее развития связывают с сороковыми годами двадцатого столетия. Отправной, наиболее крупной и значимой работой в этой области считается монография Л.В.Канторовича «Математические методы организации и планирования производства», вышедшая в 1939 году (в 1975 году Л.В.Канторовичу за цикл работ в области оптимального использования ресурсов в экономике была присуждена Нобелевская премия). Но уже в 1930 году советский ученый А.Н.Толстой предложил модель транспортной задачи. В зарубежной научной практике одним из пионеров в области линейного программирования был Джон фон Нейман, знаменитый математик и физик, успешно работавший в области теории игр, тесно связанной с методами линейного программирования. В зарубежной научной литературе ключевой обычно считается работа Дж.Данцига, вышедшая в 1947 году и посвященная решению линейных экстремальных задач, в которой автор, опираясь на методы линейной алгебры, смог сформулировать и развить «симплексный метод».

Оптимизировать – значит улучшить, получить наилучшее из имеющихся альтернативных решений. При этом задача, стоящая перед исследователем, должна быть строго формализована и представлена в виде математической модели.

В методах оптимизации поиск оптимального решения называется программированием. Содержание процедур, которые описываются в рамках этого термина, отличается от процесса программирования в области информатики, когда результатом действия является детально расписанный алгоритм расчета. Пожалуй, общим между программированием в методах оптимизации и в информатике является поиск наиболее эффективной упорядоченности процедур, необходимых для получения конкретного результата. Термин «программирование» был предложен Вудом и Данцигом, при этом подчеркивалось, что основным здесь является планирование, составление программы действий.

Задача оптимизации записывается следующим образом:

,

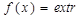т.е. равнозначны два варианта задачи:

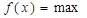
или .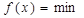

Теория задач на оптимизацию наибольших или наименьших величин называется теорией экстремальной оптимизации, что подчеркивает общность процесса оптимизации с процедурой нахождения экстремума (в курсе математического анализа). Различия между целями нахождения минимума и максимума нет, так как любая функция, имеющая, например, максимум при каком-то значении аргумента х, будучи умноженной на -1, имеет минимум в той же точке.

Типы моделей. Математическая модель – одно или система уравнений, отражающих количественную связь между входящими в модель параметрами. Целью составления модели является исследование взаимозависимости между ними, а также исследование управления процессами, которые описываются данными моделями. Уровень точности и результативности конкретной математической модели существенно зависят от ряда факторов, в том числе:

- полноты учета независимых параметров;

- точности исходных параметров;

- видов и методов математического аппарата, привлекаемого для составления модели.

По количеству независимых параметров модели подразделяют на следующие типы:

- одномерная модель отражает положение точки на числовой оси,

(например, х=а);

- двумерная модель отражает положение точки на плоскости,

(например, ах₁ +bх₂ =с);

- трехмерная модель отражает положение точки на какой-то поверхности,

(например, ах₁ + bх₂ + сх₃ =d);

- многомерная модель имеет количество независимых параметров более

трех (например, ах₁ + bх₂ + сх₃ + dх₄ =е).

Очевидно, что мы можем представить в виде геометрических образов только одно-, двух- или трехмерную модели. При количестве независимых параметров более трех говорят, что такая модель описывает гиперповерхность, которая является частью гиперпространства.

Независимые параметры входят в структуру модели с различными степенями:

- если все параметры имеют степень, равную единице, то такая модель называется линейной и геометрически отражает

линию (двумерная модель)

ах₁ +bх₂ =с,

или плоскость

ах₁ + bх₂ + сх₃ =d;

- если хотя бы один параметр имеет степень, не равную единице, то такая модель называется нелинейной и геометрически она может отражать, например, замкнутую трехмерную поверхность (например, шаровая поверхность)

,

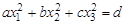или незамкнутую поверхность (например, параболоид вращения)

.

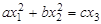Линия или поверхность, описываемые соответствующей моделью, называется линией или поверхностью отклика данной модели.

Процесс исследования модели достаточно многообразный и преследует различные цели. Поиск оптимума является одной из задач такого анализа и заключается в нахождении таких значений параметров, при которых на поверхности отклика наблюдается экстремум (максимум или минимум). В таком случае поиск экстремума может проводиться в условиях накладываемых на значения параметров ограничений либо при отсутствии таковых (т.е. зона поиска экстремума неограниченна на числовой оси). В свою очередь ограничения (как и собственно модели) могут быть линейными и нелинейными.

В зависимости от вида математических моделей и ограничений, в них имеющихся, различают линейное и нелинейное программирование. В первом случае как математическая модель, так и ограничения - это всегда линейные функции. В противном случае, если модель или хотя бы одно из ограничений описывается нелинейной функцией - говорят, что имеется задача нелинейного программирования.

Так как рассматриваемая область исследований, как правило, имеет в виду конкретные объекты, то в зависимости от типа параметров различают непрерывное и дискретное программирование. В первом случае природа рассматриваемых параметров допускает их дробность, во втором случае рассматриваются параметры только целочисленные (например, количество единиц оборудования и т.п.). Имея в своей основе общность методологических подходов, дискретное программирование требует специфических методов решения задачи.

Date: 2015-09-18; view: 341; Нарушение авторских прав