Метод Гаусса решения СЛАУ

Данный метод является более универсальным, т.к. число уравнений не обязательно должно равняться числу неизвестных, на матрицу А не накладываются никакие ограничения, т.е. рассматривается СЛАУ вида

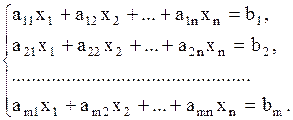(1)

Системе (1) поставим в соответствие расширенную матрицу

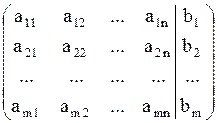(2)

Метод Гаусса основан на следующих утверждениях:

решение системы не меняется, если в матрице (2)

1) поменять строчки местами;

2) вычеркнуть в матрице нулевую строчку;

3) умножить строчку на число ;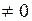

4) к элементам какой-либо строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

Правило.

Прямой ход: обнулить элементы матрицы, расположенные ниже прямой, соединяющей элементы 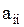(элементы с одинаковыми индексами). Т.е. привести матрицу к виду

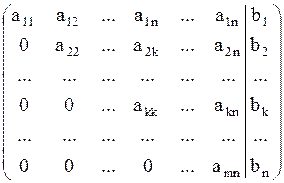
Для этого использовать перечисленные утверждения.

Обнуление элементов первого столбца производить с помощью первой строки, второго столбца – с помощью второй строки и т.д.

Способ обнуления см. в примерах.

Обратный ход: строки матрицы (начиная с нижней) поочередно представлять в виде уравнений, из которых находить неизвестные.

Замечание: в методе Гаусса работаем только со строчками, т.е. обнуление производим в столбцах.

Пример 1. Решить систему методом Гаусса.

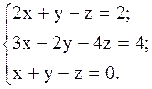
Решение. Запишем расширенную матрицу системы:

Прямой ход:

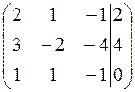
Обнулим элементы первого столбца (3 и 1) с помощью первого элемента первой строки. Обнуление с помощью элемента 2 производить не удобно, т.к. придется умножать на дробное число. Удобнее, чтобы на месте элемента 2 стояла 1 (или (-1)). Поэтому поменяем первую и третью строчки местами.

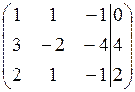
Чтобы обнулить элемент 3 в первом столбце второй строки умножим первую строку на (-3) и прибавим ко второй строке. Для обнуления элемента 2 в первом столбце третьей строки умножим первую строчку на (-2) и прибавим к третьей строке.

Обнулим элементы второго столбца с помощью второго элемента второй строки. Обнуление с помощью элемента (-5) производить не удобно. Поэтому поменяем вторую и третью строчки местами.

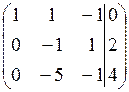
Чтобы обнулить элемент (-5) во втором столбце третьей строки умножим вторую строку на (-5) и прибавим к третьей строке.

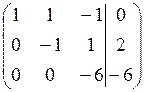
Более кратко все преобразования можно оформить следующим образом:

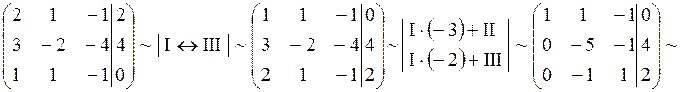
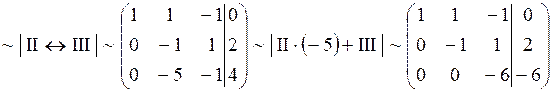
Обратный ход:

Последняя строка матрицы записывается в виде уравнения

,

.

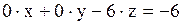
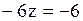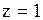Запишем в виде уравнения вторую строку матрицы

.

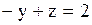Подставим полученное значение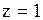

,

,

.

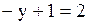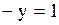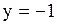Представим первую строку матрицы в виде уравнения

.

Подставив полученные значения 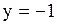и 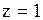, найдем значение неизвестного .

,

.

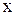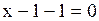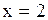Ответ: .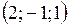

Некоторые частные случаи:

Пример 2. Решить систему методом Гаусса.

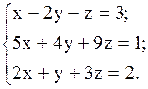
Решение.

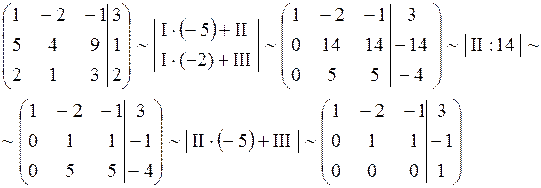
Если последнюю строку представить в виде уравнения, то получим 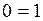, которое не может выполняться ни при каких значениях .

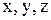Ответ: нет решения.

Пример 3. Решить систему методом Гаусса.

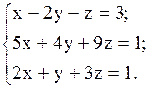
Решение.

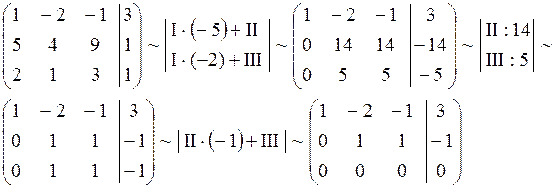
Последняя строка представляет собой уравнение 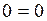. Данное уравнение не дает информацию о неизвестных 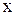, 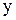и 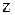, поэтому последнюю строчку можно вычеркнуть.

, ,

, ,

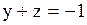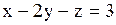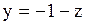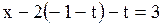пусть , ,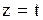

, .

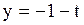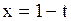Ответ: система имеет бесконечное множество решений , .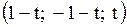

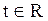Пример 4. Решить систему методом Гаусса.

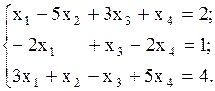
Решение.

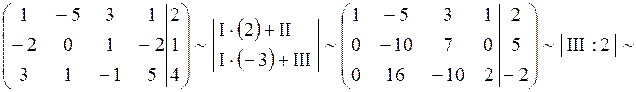
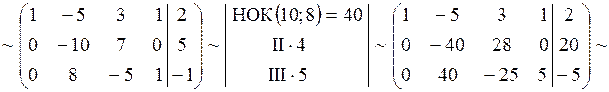
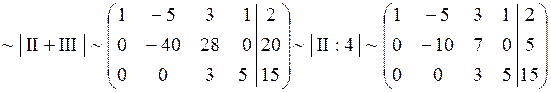
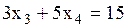, пусть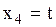

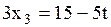
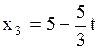
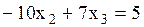
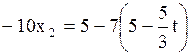
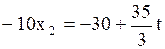
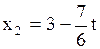
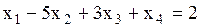
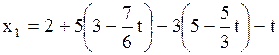
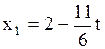
Ответ: система имеет бесконечное множество решений ,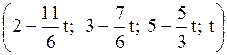

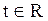
Пример 5. Решить систему методом Гаусса.

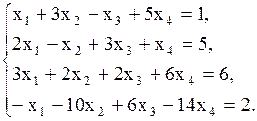
Решение.

,

,

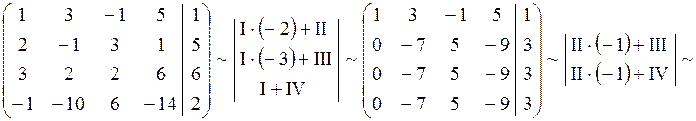
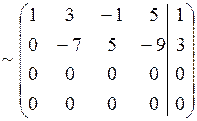
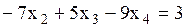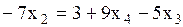пусть , ,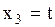

,

,

,

,

,

.

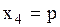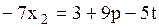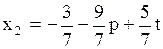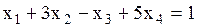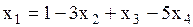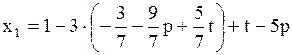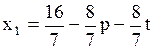Ответ: система имеет бесконечное множество решений , .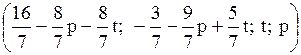

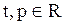Выводы:

1) Если в результате решения методом Гаусса получается строка, в которой слева от вертикальной черты расположены нули, а справа – число, отличное от нуля, то система не имеет решения; (пример 2).

2) Если в результате прямого хода получается матрица, количество строк которой равно количеству столбцов слева от черты, т.е. получается верхнетреугольная матрица, то система имеет единственное решение, т.е. система определена (пример 1).

3) Если в результате прямого хода получается матрица, число строк которой меньше числа столбцов слева от черты, то система имеет бесконечное множество решений, т.е. система неопределена (примеры 3, 4, 5).

Date: 2015-09-18; view: 1761; Нарушение авторских прав