Составление математической модели по уравнениям материального и теплового балансов(аналитическим методом)

Рассмотрим на примере теплообменника с разделенными пространствами для теплоносителя и продукта без фазовых превращений и с идеальным перемешиванием в обоих пространствах (см. рис. 2).

Введем обозначения:

Gt - массовый расход теплоносителя;

Ttn, Ttk - температура теплоносителя на входе и выходе теплообменника;

Gp - массовый расход продукта;

Tpn, Tpk - температура продукта на входе и выходе теплообменника;

ct, cp, cs - теплоемкости теплоносителя, продукта и стенки (считаем постоянными);

Mt, Mp, Ms - массы теплоносителя и продукта в теплообменнике, а также стенки между теплоносителем и продуктом (считаем постоянными);

Ts- среднее значение температуры стенок между

теплоносителем и продуктом;

Stp - площадь стенки между теплоносителем и продуктом;

ats, aps - коэффициенты теплоотдачи от теплоносителя к стенке и от стенки к продукту (считаем постоянными);

t - время.

Уравнения теплового баланса для малого интервала времени Dt

Для теплоносителя:

.

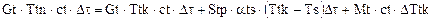Для продукта:

.

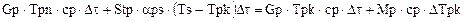Для стенки:

.

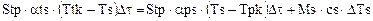Разделив левые и правые части уравнений на 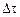и переходя к пределу при 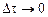получим дифференциальные уравнения, которые перепишем в привычной форме:

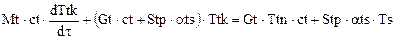, (1.1)

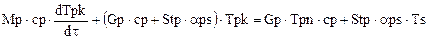, (1.2)

. (1.3)

Приведенные уравнения являются нелинейными, поскольку они содержат произведения переменных величин. Чтобы их линеаризовать можно применить разложение в ряд Тейлора или все переменные величины представить в виде суммы некоторых постоянных номинальных (средних) значений и малых приращений:

, , , , , , .

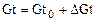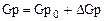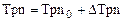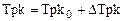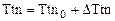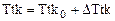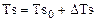Подставляя выражения для переменных величин в уравнения (1.1) – (1.3), раскрывая скобки и опуская произведения приращений, т.к. они имеют второй порядок «малости», получим:

,

,

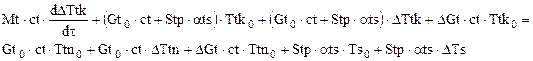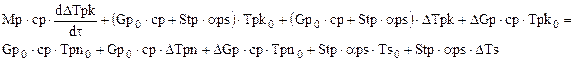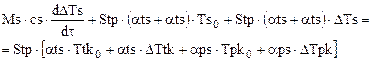
Если приращения равны нулю, то получим уравнения для установившегося состояния или уравнения статики:

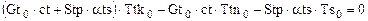, (1.4)

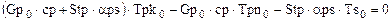, (1.5)

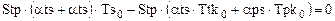. (1.6)

По уравнениям статики следует проверять правильность выбора параметров теплообменника, а также значения температур и расходов в установившемся режиме. Они могут использоваться для расчета температур стенки и теплоносителя на выходе из теплообменника, а также необходимого расхода теплоносителя.

С учетом этих уравнений статики из исходных дифференциальных уравнений в приращениях удалим постоянные слагаемые и получим линеаризованные уравнения динамики в приращениях (для упрощения записи опустим символ ∆):

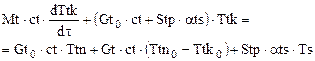, (1.7)

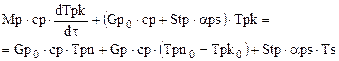, (1.8)

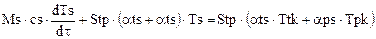. (1.9)

А. Уравнения в системе (1.7) – (1.9) путем деления их левых и правых частей на множитель при переменной величине в левой части уравнения и подстановки численных значений параметров приводятся к виду:

,

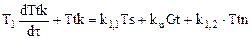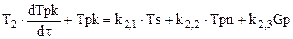, (1.10)

,

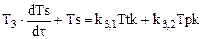где 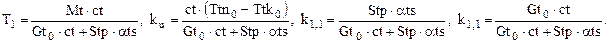Аналогично определяются коэффициенты для второго и третьего уравнений системы (1.10).

Представление математического описания в виде (1.10) позволяет достаточно просто решать систему численным методом.

Б.Переменные величины или функции 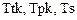являются переменными состояния объекта и полученная система уравнений соответствует математическому описанию в переменных состояния объекта. Чтобы привести уравнения (1.7) – (1.9) к стандартному виду

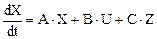, (1.11)

где X, U, Z – векторы переменных состояния, управления и возмущения; А, В и С – матрицы коэффициентов, - необходимо слева от знака равенства оставить только производные, а справа - слагаемые, содержащие переменные состояния, затем слагаемые с управляющими воздействиями и последние слагаемые – с возмущающими воздействиями. В качестве управления чаще всего выступает расход теплоносителя, а начальные температуры и расход продукта обычно являются возмущениями.

, (1.12)

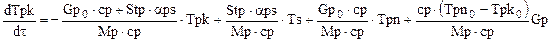, (1.13)

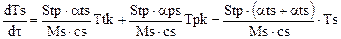. (1.14)

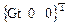В этих уравнениях вектор переменных состояния имеет вид ; вектор управления - ; вектор возмущений - ,

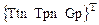матрица А = , (1.15)

матрица В = 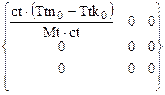, (1.16)

матрица С = 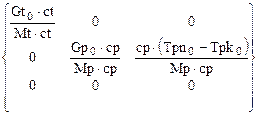. (1.17)

Математическое описание в переменных состояния применяется при синтезе оптимальных систем с различными критериями оптимальности.

В. Чтобы получить математическое описание в виде зависимости выхода объекта Tpk от управления Gt и возмущений Ttn, Tpn, Gp или в виде соответствующих передаточных функций можно исключить из уравнений (1.7) – (1.9) промежуточные переменные Ttk и Ts и получить одно уравнение третьего порядка для Tpk. Это проще всего выполнить переходя к преобразованиям Лапласа в уравнении (1.11). Так как уравнение записано для приращений, все начальные значения переменных равны нулю, что удовлетворяет требованиям для передаточной функций.

Уравнение (1.11) в преобразованиях Лапласа

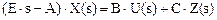, (1.18)

где Е – единичная матрица, s – комплексная переменная Лапласа.

Из (1.18) достаточно просто найти вектор X(s) используя операции с матрицами системы Mathcad 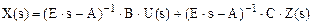. (1.19)

Для этого необходимо задать численные значения всем параметрам, используемым в матрицах А, В и С, записать выражения (1.15) - (1.17), используя символ присвоения «: =», описать векторы и выражение для определения вектора Х:

,

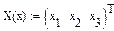
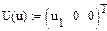
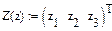
а затем вывести Х: .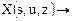

У вектора Х вторая строка вида

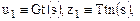
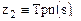
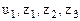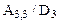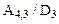соответствует выражению для изображения по Лапласу выхода объекта Tpk, а . Выражения перед являются передаточными функциями от соответствующего входа к выходу объекта. Чтобы привести передаточные функции к привычному виду необходимо их числители и знаменатели разделить на D₃, помимо этого из числителей третьей и четвертой функций в качестве коэффициентов передачи следует вынести и , соответственно.

Поскольку теплообменник является устойчивым объектом, то все коэффициенты в знаменателях передаточных функций должны быть положительными.

Математическое описание в виде передаточных функций используется при синтезе систем по частотным характеристикам, синтезе систем при случайных воздействиях и т.п.

Date: 2015-09-18; view: 693; Нарушение авторских прав