Энергии Гельмгольца и Гиббса

5.1. Постановка проблемы.

Наша система может совершать различные виды работы, как в отдельности, так и суммарно

а) известную уже работу расширения

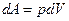
б) механическую против силы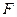

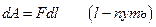
или кинетическую

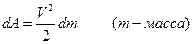
в) работу изменения поверхности системы

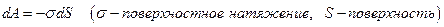
г) работу переноса электрического заряда 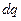в точку с потенциалом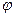

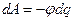
д) работу перемещения тела массой 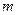на высоту над поверхностью Земли: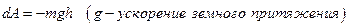

е) работу химической реакции при изменении числа молей некоторого веществ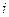а на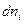

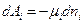
Назовем величины, которые стоят перед знаком дифференциала в правых частях равенств обобщенными силами, а величины под знаком дифференциала обобщенными координатами, тогда мы можем записать, что общая работа, которую может совершать система:

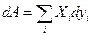
где 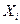-обобщенная сила, -обобщенная координата. Заметим, что 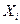-интенсивное свойство, а -экстенсивное свойство. Кроме того, один вид работы системы может быть источником другой работы: расширение газа поднимает груз на высоту. Именно этим работа отличается от теплоты: «теплота она и в Африке теплота». Мы уже знаем, что если система может совершать только работу изменения объема, то

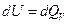или

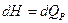
Если система адиабатическая, то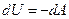

а для изотермической системы нужно знать хотя бы уравнение состояния, если система может совершать только работу изменения объема. Иными словами, необходимо найти функцию состояния, изменение которой бы соответствовало работе изотермического процесса системы при любых условиях.

5.2. Решение проблемы. Энергия Гельмгольца.

Объединим аналитические выражения для первого 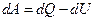и второго 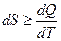законов термодинамики:

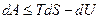
т.е. для равновесного процесса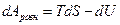

а для неравновесного процесса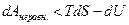

Следовательно: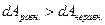

и система может совершать максимальную работу, если протекает равновесный процесс. Для того чтобы найти функцию состояния, изменение которой равно максимальной работе изотермического процесса, необходимо выражение для объединенного I и II законов преобразовать так, чтобы температура стала независимой переменной, т.е. попала бы под знак дифференциала. Похожую операцию мы уже делали, когда вводили энтальпию. Итак:

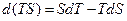
и подстановка 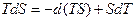дает:

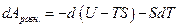
Выражение, стоящее в круглых скобках, имеет свойства функции состояния и носит название энергия Гельмгольца

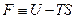
Легко видеть, что если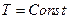

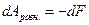
т.е. максимальная положительная работа изотермического процесса равна убыли энергии Гельмгольца системы.

Поскольку 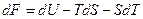то подстановка в объединенное уравнение I и II закона дает

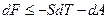
Очевидно, что если неизолированная изотермическая система не совершает работу (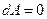), то

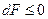
т.е. в этом случае самопроизвольный неравновесный процесс может идти только в сторону уменьшения энергии Гельмгольца системы, а равновесие наступает когда энергия Гельмгольца принимает минимальное значение (dF = 0)

Если система совершает только работу расширения 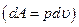, то

а коэффициент объемного термического расширения

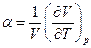
и изотермическая сжимаемость

Полезно также помнить, что

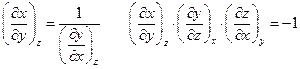
Частные производные химической термодинамики чрезвычайно полезны при решении самых разнообразных задач.

Например, изменится ли изобарная теплоемкость вещества, если увеличить давление:

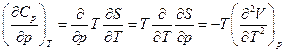
т.е. если коэффициент термического расширения зависит от температуры

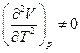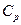, то изменится, иными словами, необходимо иметь очень точное уравнение состояния данного вещества.

Другая задача: жидкая вода, взятая при температуре 0 ⁰С адиабатически сжимается до давления 1000 атм. Как изменится ее температура? Адиабатический процесс является изэнтропическим процессом, поэтому для ответа на вопрос необходимо оценить производную .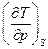

Имеем

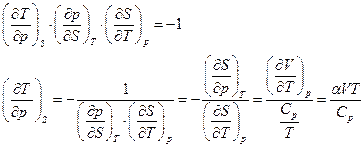
Для воды и

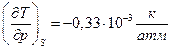. Следовательно температура жидкой воды понизится при адиабатическом сжатии до 1000 атм. примерно до –0,3 ⁰С. Замерзнет ли при этом жидкая вода?

5.5. Уравнение Гиббса-Гельмгольца.

По определению

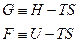
Отсюда: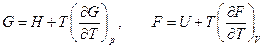

Эти уравнения позволяют найти связь между максимальной работой процесса, протекающего равновесно, и тепловым эффектом этого же процесса.

Для обратимого изотермического процесса перехода системы из состояния 1 в состояние 2 при 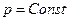имеем:

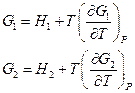
Отсюда

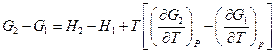, т.е.

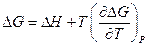
Аналогично

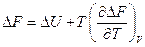
Последние два уравнения носят название уравнений Гиббса-Гельмгольца и

связывают максимальные работы равновесных процессов с тепловыми эффектами неравновесных процессов, протекающих между теми же начальным и конечным состояниями, но без совершения работы или с совершением только работы расширения.

Уравнениям Гиббса-Гельмгольца можно придать другую форму

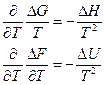
В дальнейшем этими уравнениями мы будем часто пользоваться.

а коэффициент объемного термического расширения

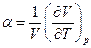
и изотермическая сжимаемость

Полезно также помнить, что

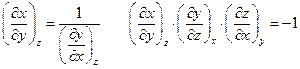
Частные производные химической термодинамики чрезвычайно полезны при решении самых разнообразных задач.

Например, изменится ли изобарная теплоемкость вещества, если увеличить давление:

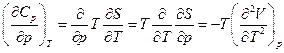
т.е. если коэффициент термического расширения зависит от температуры

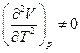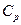, то изменится, иными словами, необходимо иметь очень точное уравнение состояния данного вещества.

Другая задача: жидкая вода, взятая при температуре 0 ⁰С адиабатически сжимается до давления 1000 атм. Как изменится ее температура? Адиабатический процесс является изэнтропическим процессом, поэтому для ответа на вопрос необходимо оценить производную .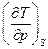

Имеем

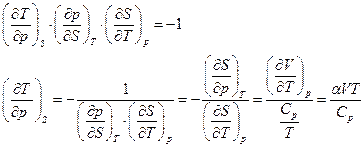
Для воды 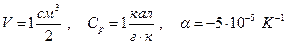и

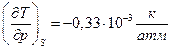. Следовательно температура жидкой воды понизится при адиабатическом сжатии до 1000 атм. примерно до –0,3 ⁰С. Замерзнет ли при этом жидкая вода?

5.5. Уравнение Гиббса-Гельмгольца.

По определению

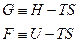
Отсюда: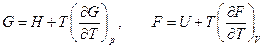

Эти уравнения позволяют найти связь между максимальной работой процесса, протекающего равновесно, и тепловым эффектом этого же процесса.

Для обратимого изотермического процесса перехода системы из состояния 1 в состояние 2 при 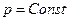имеем:

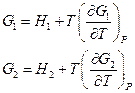
Отсюда

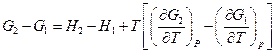, т.е.

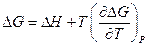
Аналогично

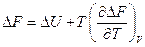
Последние два уравнения носят название уравнений Гиббса-Гельмгольца и

связывают максимальные работы равновесных процессов с тепловыми эффектами неравновесных процессов, протекающих между теми же начальным и конечным состояниями, но без совершения работы или с совершением только работы расширения.

Уравнениям Гиббса-Гельмгольца можно придать другую форму

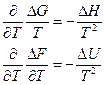
В дальнейшем этими уравнениями мы будем часто пользоваться.

Date: 2015-09-18; view: 548; Нарушение авторских прав