Лемма 3

1. Если 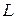– подпространство в .

2. Если подпространство 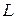не совпадает со всем векторным пространством размерности , то .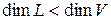

Доказательство. Методом от противного.

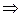
1. Если 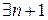независимых векторов в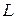 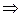они линейно независимы в , т.е. противоречие.

2. Пусть 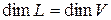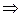по теореме 4 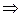любые векторов образуют базис в 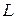. Но так как любые векторов образуют базис в они совпадают .

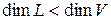Замечание. Если 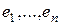– базис в , то любое подмножество 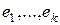является базисом некоторого подпространства 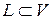базис не может быть получен простым выбором подмножества из множества 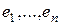. Например, 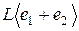. Вместе с тем, справедлива теорема.

Теорема 1. Если элементы 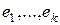составляют базис k -мерного подпространства 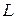пространства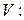 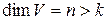, то этот базис может быть дополнен элементами 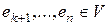так, что совокупность 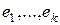, – базис .

Доказательство. Пусть 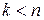. Тогда существует вектор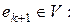 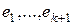– линейно независимы, так как в противном случае 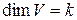. Продолжая далее указанную процедуру, получим , .

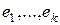Теорема 2 (о размерности линейной оболочки векторов). Размерность линейной оболочки 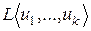равна максимальному числу линейно независимых векторов в множестве 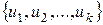. В частности, если 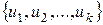– линейно независимы, то 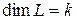и эти элементы образуют базис в .

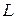Доказательство. Пусть среди элементов 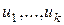есть 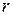линейно независимых элементов 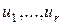и любые 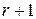элементов линейно зависимы. Добавим к 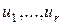произвольный элемент 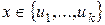. Тогда 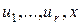– линейно зависимы, т.е.

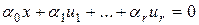и

среди 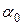, , 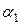…, 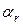хотя бы один не нуль. Очевидно, что 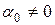(так как иначе 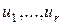– линейно зависимы)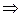 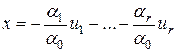, т.е. любой другой элемент 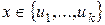может быть представлен как линейная комбинация 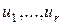. Но все элементы 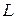имеют вид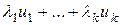 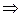подставляя здесь вместо 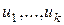их представление как линейной комбинации 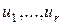. Это означает, что 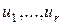– базис и что .

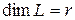2^о. Ранг матрицы как максимальное число линейно независимых строк (столбцов).

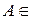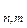Напомним, что если R , то 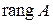– это число 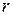, такое, что существует минор порядка 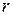, отличный от нуля и все миноры порядка 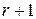равны 0.

Теорема 3. Ранг произвольной матрицы 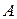равен максимальному числу линейно независимых строк (столбцов) этой матрицы.

Доказательство. Докажем для строк. Пусть

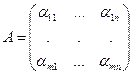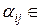, где R.

Каждую строку в 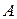можно рассматривать как элемент пространства R 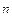(т.е. упорядоченную совокупность действительных чисел). Тогда линейная оболочка 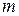строк порождает подпространство 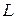. Пусть в матрице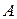 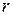базисных строк. Тогда по теореме о базисном миноре (см. §4) имеем, что любая строка матрицы 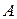является линейной комбинацией этих 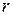строк, т.е. элементом подпространства 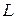, а из теоремы 2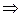 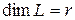. Таким образом, 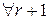строк матрицы 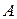линейно зависимы, т.е. 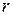– максимальное число линейно независимых строк.

Следствие. Число линейно независимых строк равно числу линейно независимых столбцов матрицы .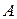

3^о. Элементарные преобразования матрицы.

Вычислять ранг матрицы перебором всех миноров – большая работа. Несколько облегчает положение метод окаймляющих миноров, согласно которому миноры 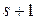порядка ищутся как окаймляющие ненулевой минор 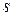–ого порядка.

Проще всего находить ранг матрицы и ее базисный минор при помощи элементарных преобразований.

Определение 3. Элементарными преобразованиями матрицы называются следующие преобразования:

1. Умножение строки на элемент 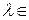R, отличный от нуля.

2. Прибавление к одной строке другой строки.

3. Перестановка строк.

4. Такие же преобразования над столбцами.

Теорема 4. Элементарные преобразования не меняют ранга матрицы.

Доказательство. Пусть 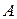– исходная матрица, 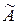– преобразованная, 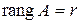, т.е. 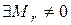и все , ,…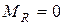

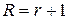1. Если 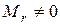, то если умноженная строка входит в 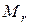, то 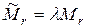, если нет, то 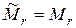. Для имеем .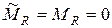

2. Пусть 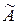получается из 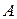прибавлением к –ой строке 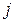–ой. Покажем, что при этом ранг не увеличивается, т.е. если .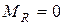

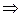
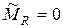а) Если 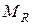содержит и -ую и 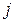-ую строки – очевидно, что .

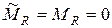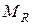б) Если –ая строка не входит в , то .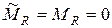

в) Если –ая входит в 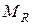, а 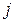–ая – не входит, то 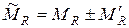, где 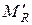– другой минор матрицы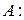 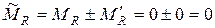. Знак “-” может возникнуть из-за того, что 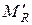могут быть переставлены строки. Например,

.

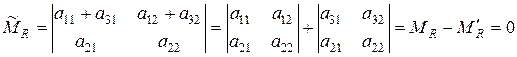Т.о. 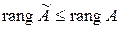, т.е. прибавление строк – обратимая операция, то 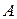получается из 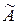такой же операцией, т.е. .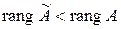

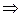
3. Очевидно, что при перестановке двух строк не меняется максимальное число линейно независимых строк.

4. Неизменность ранга при элементарных преобразованиях столбцов доказывается аналогично.

Определение 4. Матрицы 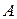и 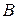, получаемые друг из друга элементарными преобразованиями, называются эквивалентными.

Т.о., эквивалентные матрицы имеют одинаковый ранг.

Определение 5. Матрица, у которой в каждой следующей строке, начиная со второй, первый отличный от нуля элемент стоит правее первого отличного от нуля элемента предыдущей строки, а все нулевые строки (т.е. строки, содержащих хотя бы один ненулевой элемент), называется ступенчатой.

Пример:

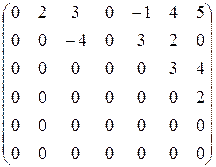– ступенчатая матрица.

Теорема 5 (о ступенчатой матрице).

1. Каждая матрица элементарными преобразованиями строк приводится к ступенчатой.

2. Ранг ступенчатой матрицы равен числу ненулевых строк.

Доказательство. 1) Если некоторый элемент 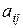данной матрицы отличен от нуля, то с помощью элементарных преобразований строк можно получить новую матрицу, в которой все элементы, стоящие над 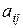и под ним равны нулю. Например, чтобы получить нуль на месте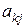 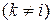, достаточно умножить –ую строку на 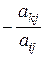и прибавить к 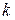-ой строке. На месте 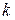-ого элемента будет стоять .

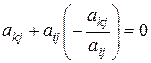Возьмем первый слева ненулевой столбец и переставим строки так, чтобы в первой строке оказался этот ненулевой элемент (если первый элемент этого столбца был ненулевым, то переставлять строки не надо). Элементарными преобразованиями все элементы столбца можно сделать нулями. Первая строка ступенчатой матрицы готова: все ненулевые элементы второй и нижних строк стоят правее первого ненулевого элемента первой строки.

Применим ту же процедуру к матрице, начиная со второй строки: возьмем первый слева столбец, содержащий ненулевые элементы, переставим так, чтобы во второй строке был ненулевой элемент и т.д. После этого будет готова и вторая строка.

Так как строк конечное число, то процесс конечен.

2) Пусть в ступенчатой матрице 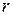ненулевых строк. Тогда любой минор 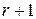и выше порядков равен 0, т.е. содержит нулевые строки. Ненулевой минор 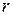-ого порядка строится так: берутся столбцы, содержащие первые ненулевые элементы 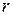ненулевых строк. Его определитель равен произведению этих ненулевых элементов (верхнетреугольная матрица). Т.о., . ■

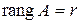Пример. В выше рассмотренном примере 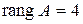. Т.о., ранг любой матрицы вычисляется приведением ее к ступенчатому виду.

Т.е., ранг 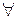матрицы вычисляется приведением её к ступенчатому виду.

Date: 2015-09-03; view: 407; Нарушение авторских прав