
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Ряды динамики
|
|
Б.3 Б.4 СТАТИСТИКА
Статистические методы анализа динамики социально-экономических явлений и процессов
Методические указания
Направление подготовки бакалавра
Экономика
Уфа 2012
УДК 311
ББК 60.6
А 14
Рекомендовано к изданию методической комиссией экономического факультета (протокол № 5 от «19» февраля 2012 г.)
Составитель: к.э.н., доцент А.М. Аблеева
Рецензент: к.э.н., доцент кафедры бухгалтерского учета и аудита
Насырова А.Д.
Ответственный за выпуск: заведующий кафедрой статистики и информационных систем в экономике к.э.н., доцент А.М. Аблеева
ВВЕДЕНИЕ
Ряд динамики, хронологический ряд, динамический ряд, временной ряд – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития социально-экономического явления. При изучении явления во времени исследователь часто сталкивается с необходимостью описать интенсивность изменения явления и выявить основную тенденцию его развития.
Цель работы: выявить основную тенденцию развития динамики исследуемого явления с использованием пакетов прикладных программ «EXCEL», «STRAZ» и выполнить прогноз на перспективу.
Задачи:
- рассчитать показатели изменения уровней ряда динамики;
- выполнить выравнивание ряда динамики исследуемого явления с помощью методов механического выравнивания и плавного уровня;
- провести аналитическое выравнивание ряда динамикис использованием пакетов прикладных программ «EXCEL», «STRAZ»; отобрать функцию в качестве тренда;
- на основе отобранной функции в качестве тренда, рассчитать показатели колеблемости и сделать прогноз с расчетом точечных прогнозов и доверительных интервалов прогнозной оценки.
РЯДЫ ДИНАМИКИ
Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Для отображения динамики строят ряды динамики.
Ряд динамики – ряд числовых значений определенного статистического показателя в последовательные моменты или периоды времени.
Составными элементами ряда динамики являются показатели уровней ряда (У) и периоды времени (годы, месяцы, сутки) или моменты (даты) времени (t).
Ряды динамики можно классифицировать по следующим признакам.
1. В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.
2. В зависимости от того, как выражают уровни ряда состояние явления на определенные моменты времени (на начало месяца, года и т.п.) или его величину за определенные интервалы времени (за сутки, месяц, год и т. п.), различают соответственно моментные и интервальные ряды динамики.
3. В зависимости от расстояния между уровнями ряды динамики подразделяются на ряды динамики с равноотстоящими уровнями и неравноотстоящими уровнями во времени.
Анализ скорости и интенсивности развития явления во времени осуществляется с помощью статистических показателей, которые получаются в результате сравнения уровней между собой. К таким показателям относятся: абсолютный прирост, темп роста, темп прироста и абсолютное значение одного процента прироста (таблица 1.1). При этом принято сравниваемый уровень называть отчетным, а уровень с которым производят сравнение, - базисным.
Таблица 1.1 Способы расчета показателей ряда динамики
| Показатели | Способы расчета | |
| базисный | цепной | |
| Абсолютный прирост, ц | 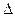 б = Уi – У1 б = Уi – У1
| 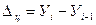
|
| Средний абсолютный прирост, ц | 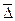 б= б= 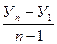
| 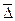 ц = ц = 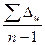
|
| Темп роста, % | 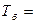 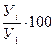
| 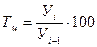
|
| Средний темп роста, % | 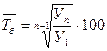
| 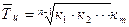
|
| Темп прироста, % | 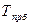 = = 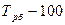
| 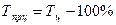
|
| Средний темп прироста, % | 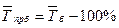
| 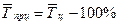
|
| Абсолютное содержание 1% прироста, ц | - | 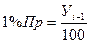
|
где У1 – начальный уровень ряда;
Уn – конечный уровень ряда;
Уi – i-ый уровень ряда;
n – число лет, или число уровней ряда;
кi – цепные темпы роста;
m – количество цепных темпов роста.
Тенденция развития или тренд – изменения динамического ряда, определяющие некое общее направление развития, которая пробивает себе дорогу через другие систематические и случайные колебания.
Тренд – это долговременная компонента ряда динамики, характеризующая основную тенденцию его развития.
При изучении в рядах динамики основной тенденции развития явления во времени применяются различные приемы и методы. Методы выравнивания (сглаживания) разделяются на две основные группы:
1) механическое выравнивание отдельных членов ряда динамики с использованием фактических значений соседних уровней;
2) аналитическое выравнивание с применением кривой, проведенной между конкретными уровнями таким образом, чтобы она отображала тенденцию, присущую ряду, и одновременно освободила его от незначительных колебаний.
Механическое выравнивание проводится методом укрупнения интервалов и методом скользящей средней.
Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда, так как в силу влияния различных факторов, в рядах динамики наблюдаются снижение и повышение уровней, которые мешают видеть основную тенденцию развития изучаемого явления.
Метод скользящей средней состоит в укрупнении периодов, образованных последовательным исключением начального уровня ряда и замены его очередным. Например, если выравнивание проводится по трем членам ряда, то новый будет:
Х1 = Х1+Х2+Х3 / 3 Х2 = Х2+Х3+Х4 / 3 и т.д.
Метод плавного уровня заключается в выравнивании ряда динамики двумя способами:
1. По среднему абсолютному приросту:
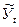 = У0 +
= У0 + 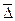 t,
t,
где 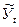 - выравненное (расчетное) значение анализируемого фактора;
- выравненное (расчетное) значение анализируемого фактора;
У0 – начальный уровень ряда динамики;
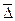 - средний абсолютный прирост;
- средний абсолютный прирост;
t - порядковый номер года.
2. По среднему коэффициенту роста:
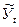 = У0 * к t
= У0 * к t
где к – средний коэффициент роста.
Аналитическое выравнивание основано на том, что уровни ряда динамики выражаются в виде функции времени. Функцию выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.
При выравнивании обычно используются следующие зависимости: линейная, параболическая, гиперболическая, экспоненциальная.
Оценка параметров уравнения осуществляется в большинстве случаев с использованием метода наименьших квадратов, который обеспечивает наименьшую сумму квадратов отклонений фактических уровней от выравненных: (У – Уt) ----> min
Для проявления тенденции динамики можно использовать уравнение прямой:
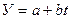 ,
,
где - 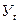 - выравненное значение анализируемого фактора,
- выравненное значение анализируемого фактора,
a, b – неизвестные параметры;
a – значение выравненной урожайности для центрального в динамическом ряду года, содержательной интерпретации не имеет;
b – ежегодный прирост (снижение) урожайности;
t – значения дат.
Для определения неизвестных параметров a и b в соответствии с требованием способа наименьших квадратов необходимо решить систему нормальных уравнений:
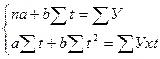
Система упрощается, если воспользоваться способом отсчета времени от условного начала.
Поскольку 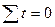 , то система уравнений принимает вид:
, то система уравнений принимает вид:
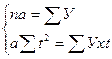 , тогда
, тогда  ,
, 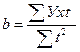 .
.
При правильном выборе уравнения сумма фактических значений урожайности 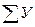 должна максимально приближаться к сумме расчетных значений урожайности
должна максимально приближаться к сумме расчетных значений урожайности 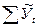 .
.
Для отбора функции в качестве тренда можно использовать способ сравнения остаточных дисперсий по различным функциям по критерию F Фишера. При сравнении фактического и табличного значения критерия Фишера с учетом степеней свободы делается вывод о предпочтении какому-либо способу выравнивания.
Также отобрать функцию в качестве тренда можно с помощью минимального значения остаточного среднеквадратического отклонения или коэффициента колеблемости.
Для выполнения прогноза следует по выбранной функции получить прогнозные оценки: точечные прогнозы и доверительные интервалы прогноза.
Границы тренда имеют вид: 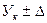 ,
,
где Ук – точечный прогноз на к- период;
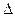 - доверительные интервалы прогноза.
- доверительные интервалы прогноза.
Величина доверительного интервала определяется:
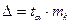 ,
,
где 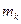 - ошибка прогноза.
- ошибка прогноза.
Для прямолинейного тренда ошибка прогноза находится по формуле:
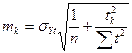 ;
;
для параболы: 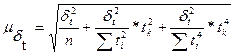 ,
,
где ta - табличное значение t - критерия Стьюдента при уровне значимости a (находится по таблице с учетом степеней свободы v = п- р);
tk – номер прогнозируемого периода;
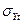 - среднее квадратическое отклонение от тренда;
- среднее квадратическое отклонение от тренда;
п - число уровней ряда;
р - число параметров уравнения тренда.
Date: 2015-09-03; view: 514; Нарушение авторских прав