
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифференциальные уравнения движения материальной точки
|
|
Динамика. Основные понятия и определения.
Динамикой называется раздел механики, в котором изучаются законы движения материальных тел под действием сил. В разделе динамики решается более сложная и важная задача. Определяется движение тела под действием сил приложенных к нему, с учетом внешних и внутренних условий, влияющих на это движение, включая самих материальных тел.
Инертность и представляет собой свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Если, например, при действии одинаковых сил изменение скорости первого тела происходит медленнее, чем второго, то говорят, что первое тело является более инертным, и наоборот.
Количественной мерой инертности данного тела является физическая величина, называемая массой тела. В механике масса m рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.
В общем случае движение тела зависит не только от его суммарной массы и приложенных сил; характер движения может еще зависеть от формы тела, точнее от взаимного расположения образующих его частиц (т. е. от распределения масс).
Чтобы при первоначальном изучении динамики иметь возможность отвлечься от учета влияния формы тел (распределения масс), вводится понятие о материальной точке.
Материальной точкой называют материальное тело (тело, имеющее массу), размерами которого при изучении его движения можно пренебречь.
Точка называется изолированной, если на точку не оказывается никакого влияния, никакого действия со стороны других тел и среды, в которой точка движется.
2. Аксиомы динамики (законы Галилея – Ньютона).
В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений над движением тел. Систематически эти законы были впервые изложены И. Ньютоном.
Первый закон (закон инерции), открытый Галилеем, гласит: изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние. Движение, совершаемое точкой при отсутствии сил, называется движением по инерции.
Закон инерции отражает одно из основных свойств материи - пребывать неизменно в движении и устанавливает для материальных тел эквивалентность состояний покоя и движения по инерции. Из него следует, что если F=0, то точка покоится или движется с постоянной по модулю и направлению скоростью ( 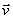 =const); ускорение точки при этом равно нулю:
=const); ускорение точки при этом равно нулю:  = 0); если же движение точки не является равномерным и прямолинейным, то на точку действует сила.
= 0); если же движение точки не является равномерным и прямолинейным, то на точку действует сила.
Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной системой отсчета (иногда ее условно называют неподвижной). (По данным опыта для нашей Солнечной системы инерциальной является система отсчета, начало которой находится в центре Солнца, а оси направлены на так называемые неподвижные звезды. При решении большинства технических задач инерциальной, с достаточной для практики точностью, можно считать систему отсчета, жестко связанную с Землей).
Второй закон (основной закон динамики) гласит: произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы.
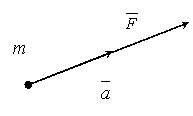
Математически этот закон выражается векторным равенством 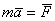 .
.
При этом между модулями ускорения и силы имеет место зависимость ma = F.
Второй закон динамики, как и первый, имеет место только по отношению к инерциальной системе отсчета. Из этого закона непосредственно видно, что мерой инертности материальной точки является ее масса, так как две разные точки при действии одной и той же силы получают одинаковые ускорения только тогда, когда будут равны их массы; если же массы будут разные, то точка, масса которой больше (т. е. более инертная), получит меньшее ускорение, и наоборот.
Если на точку действует одновременно несколько сил, то они, как известно, будут эквивалентны одной силе, т.е. равнодействующей 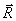 , равной геометрической сумме этих сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид
, равной геометрической сумме этих сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид
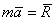 или
или 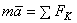 .
.
Третий закон (закон равенства действия и противодействия) устанавливает характер механического взаимодействия между материальными телами. Для двух материальных точек он гласит: две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.
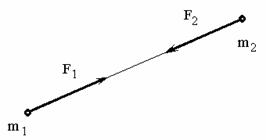
Сила, с которой материальная точка сопротивляется изменению своего движения, будем называть силой инерции этой точки - 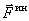 . По третьему закону она равна и противоположна действующей на точку силе
. По третьему закону она равна и противоположна действующей на точку силе  ,
, 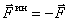 . Но на основании второй аксиомы
. Но на основании второй аксиомы 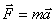 . Поэтому
. Поэтому 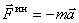 .
.
Итак, сила инерции материальной точки по величине равна произведению её массы на ускорение
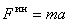 .
.
И направлена эта сила инерции в сторону противоположную вектору ускорения.
Например, при движении точки по кривой линии ускорение  . Поэтому сила инерции
. Поэтому сила инерции
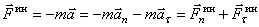 .
.
То есть её можно находить как сумму двух сил: нормальной силы инерции и касательной силы инерции.
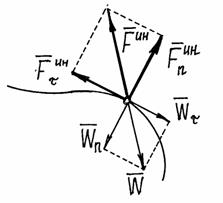
Рис.1
Третий закон динамики, как устанавливающий характер взаимодействия материальных частиц, играет большую роль в динамике системы.
Четвертый закон (закон независимого действия сил): при одновременном действии на материальную точку нескольких сил ускорение точки относительно инерционной системы отсчета от действия каждой отдельной силы не зависит от наличия других, приложенных к точке, сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил.
 ;
; 
Дифференциальные уравнения движения материальной точки.
С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки.
1) Определение движения точки координатным способом.
Рассмотрим свободную материальную точку, движущуюся под действием сил 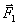 ,
, 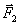 ,..,
,.., 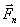 . Проведем неподвижные координатные оси Oxyz (рис.4). Проектируя обе части равенства
. Проведем неподвижные координатные оси Oxyz (рис.4). Проектируя обе части равенства  на эти оси и учитывая,что
на эти оси и учитывая,что 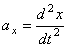 и т.д., получим дифференциальные уравнения криволинейного движения точки в проекциях на оси прямоугольной декартовой системы координат:
и т.д., получим дифференциальные уравнения криволинейного движения точки в проекциях на оси прямоугольной декартовой системы координат:
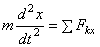 ,
, 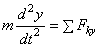 ,
, 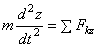 .
.
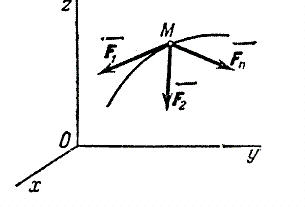
Рис.4
Так как действующие на точку силы могут зависеть от времени, от положения точки и от ее скорости, то правые части уравнений могут содержать время t, координаты точки х, у, z и проекции ее скорости  . При этом в правую часть каждого из уравнений могут входить все эти переменные.
. При этом в правую часть каждого из уравнений могут входить все эти переменные.
Чтобы с помощью этих уравнений решить основную задачу динамики, надо, кроме действующих сил, знать еще начальные условия, т.е. положение и скорость точки в начальный момент. В координатных осях Oxyz начальные условия задаются в виде: при 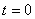
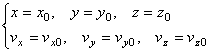 .
.
Зная действующие силы, после интегрирования уравнений найдем координаты х, y, z движущейся точки, как функции времени t, т.е. найдем закон движения точки.
2) Определение движения точки естественным способом.
Координатным способом обычно определяют движение точки, не ограниченные какими-либо условиями, связями. Если на движение точки наложены ограничения, на скорость или координаты, то определить такое движение координатным способом совсем не просто. Удобнее использовать естественный способ задания движения.
Определим, например, движение точки по заданной неподвижной линии, по заданной траектории (рис. 7).
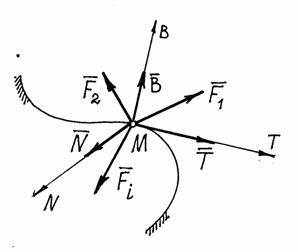
Рис.7
На точку М кроме заданных активных сил 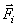 , действует реакция линии. Показываем составляющие реакции
, действует реакция линии. Показываем составляющие реакции 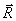 по естественным осям
по естественным осям 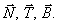
Составим основное уравнение динамики 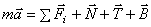 и спроектируем его на естественные оси
и спроектируем его на естественные оси

Так как 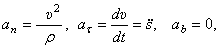 то получим дифференциальные уравнения движения, такие
то получим дифференциальные уравнения движения, такие
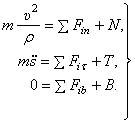 (5)
(5)
Здесь сила  - сила трения. Если линия, по которой движется точка, гладкая, то Т = 0 и тогда второе уравнение будет содержать только одну неизвестную – координату s:
- сила трения. Если линия, по которой движется точка, гладкая, то Т = 0 и тогда второе уравнение будет содержать только одну неизвестную – координату s:
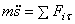 .
.
Решив это уравнение, получим закон движения точки  , а значит, при необходимости, и скорость и ускорение. Первое и третье уравнения (5) позволят найти реакции
, а значит, при необходимости, и скорость и ускорение. Первое и третье уравнения (5) позволят найти реакции 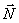 и
и  .
.
Date: 2015-09-03; view: 1972; Нарушение авторских прав