
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Некоторые частные случаи движения точки
|
|
1) Прямолинейное движение. Если траекторией точки является прямая линия, то 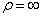 . Тогда
. Тогда 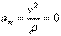 и все ускорение точки равно одному только касательному ускорению:
и все ускорение точки равно одному только касательному ускорению:
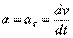 .
.
Так как в данном случае скорость изменяется только численно, то отсюда заключаем, что касательное ускорение характеризует изменение скорости по численной величине.
2) Равномерное криволинейное движение. Равномерным называется такое криволинейное движение точки, в котором численная величина скорости все время остается постоянной: 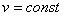 .
.
Тогда 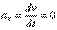 и все ускорение точки равно одному только нормальному:
и все ускорение точки равно одному только нормальному: 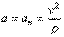 .
.
Вектор ускорения 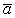 направлен при этом все время по нормали к траектории точки.
направлен при этом все время по нормали к траектории точки.
Так как в данном случае ускорение появляется только за счет изменения направления скорости, то отсюда заключаем, что нормальное ускорение характеризует изменение скорости по направлению. Найдем закон равномерного криволинейного движения.
Из формулы  имеем
имеем 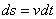 .
.
Пусть в начальный момент (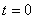 ) точка находится от начала отсчета на расстоянии
) точка находится от начала отсчета на расстоянии 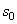 . Тогда, беря от левой и правой части равенства определенные интегралы в соответствующих пределах, получим
. Тогда, беря от левой и правой части равенства определенные интегралы в соответствующих пределах, получим
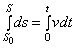 или
или 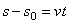 ,
,
так как 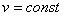 . Окончательно находим закон равномерного криволинейного движения в виде
. Окончательно находим закон равномерного криволинейного движения в виде
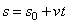 .
.
Если  , то s даст путь, пройденный точкой за время t. Следовательно, при равномерном движении путь, пройденный точкой, расчет пропорционального времени, а скорость движения равна отношению пути ко времени
, то s даст путь, пройденный точкой за время t. Следовательно, при равномерном движении путь, пройденный точкой, расчет пропорционального времени, а скорость движения равна отношению пути ко времени
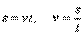 .
.
3) Равномерное прямолинейное движение. В этом случае  , а значит и
, а значит и 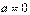 . Заметим, что единственным движением, в котором ускорение точки все время равно нулю, является равномерное прямолинейное движение.
. Заметим, что единственным движением, в котором ускорение точки все время равно нулю, является равномерное прямолинейное движение.
4) Равнопеременное криволинейное движение. Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиною постоянной: 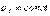 . Найдем закон этого движения, считая, что при
. Найдем закон этого движения, считая, что при  :
:  , а
, а 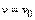 , где
, где 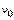 - начальная скорость точки. Согласно формуле
- начальная скорость точки. Согласно формуле 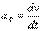 имеем
имеем 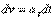 .
.
Так как  , то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим:
, то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим:
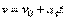 .
.
Формулу представим в виде 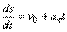 или
или 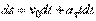 .
.
Вторично интегрируя, найдем закон равнопеременного криволинейного движения точки в виде 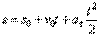 .
.
Если при криволинейном движении точки модуль скорости возрастает, то движение называется ускоренным, а если убывает - замедленным.
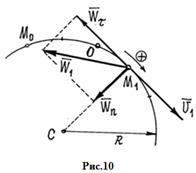 Пример 4. Точка движется по окружности радиуса
Пример 4. Точка движется по окружности радиуса  по закону
по закону 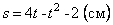 . При
. При 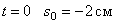 . Значит, движение началось из M 0 (рис.10).
. Значит, движение началось из M 0 (рис.10).

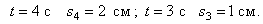
Судя по этим результатам, точка сначала двигалась в положительном направлении, а затем пошла обратно. В крайнем положении скорость точки станет равной нулю.
|
Так как 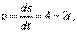 то положив
то положив  , найдём время
, найдём время 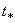 когда точка окажется в этом крайнем положении:
когда точка окажется в этом крайнем положении: 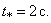 Значит
Значит 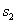 определяет это положение точки.
определяет это положение точки.
Найдём скорость и ускорение точки при 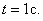 Скорость
Скорость 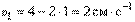 . Направлен вектор скорости в положительном направлении (
. Направлен вектор скорости в положительном направлении (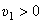 ).
).
Касательное ускорение  . Вектор
. Вектор 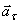 направлен в отрицательном направлении. Нормальное ускорение
направлен в отрицательном направлении. Нормальное ускорение 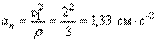 (радиус кривизны дуги окружности равен её радиусу
(радиус кривизны дуги окружности равен её радиусу  ). Полное ускорение
). Полное ускорение 
Так как вектор скорости 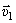 и вектор касательного ускорения
и вектор касательного ускорения 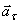 направлены в противоположные стороны, точка в этот момент движется замедленно.
направлены в противоположные стороны, точка в этот момент движется замедленно.
1. Вращение твердого тела (по заданному закону φ= φ(t), уметь определять угловую скорость, угловое ускорение, линейную скорость и ускорение точки тела).
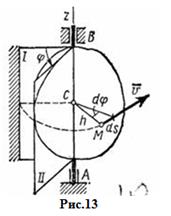 Вращательным движением твердого тела вокруг неподвижнойоси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными (рис.13).
Вращательным движением твердого тела вокруг неподвижнойоси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными (рис.13).
Проходящая через неподвижные точки А и В прямая АВ называется осью вращения.
Так как расстояния между точками твердого тела должны оставаться неизменными, то очевидно, что при вращательном движении все точки, принадлежащие оси вращения, будут неподвижны, а все остальные точки тела будут описывать окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси.
Для определения положения вращающегося тела проведем через ось вращения, вдоль которой направим ось  , полуплоскость - неподвижную и полуплоскость, врезанную в само тело и вращающуюся вместе с ним (рис. 13).
, полуплоскость - неподвижную и полуплоскость, врезанную в само тело и вращающуюся вместе с ним (рис. 13).
Тогда положение тела в любой момент времени однозначно определится взятым с соответствующим знаком углом  между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол
между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол  положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси
положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси  ), и отрицательным, если по ходу часовой стрелки. Измерять угол
), и отрицательным, если по ходу часовой стрелки. Измерять угол  будем всегда в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла
будем всегда в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла  от времени t, т.е.
от времени t, т.е.  .
.
Уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси.
Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость  и угловое ускорение
и угловое ускорение 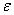 .
.
Если за промежуток времени  тело совершает поворот на угол
тело совершает поворот на угол  , то численно средней угловой скоростью тела за этот промежуток времени будет
, то численно средней угловой скоростью тела за этот промежуток времени будет  . В пределе при
. В пределе при 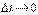 найдем, что
найдем, что 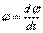 или
или 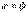 .
.
Таким образом, числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени. Знак  определяет направление вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки,
определяет направление вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки,  >0, а когда по ходу часовой стрелки, то
>0, а когда по ходу часовой стрелки, то  <0.
<0.
Размерность угловой скорости 1/Т (т.е. 1/время); в качестве единицы измерения обычно применяют рад/с или, что тоже, 1/с (с-1), так как радиан - величина безразмерная.
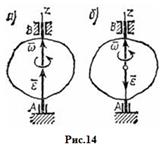
Угловую скорость тела можно изобразить в виде вектора  , модуль которого равен |
, модуль которого равен |  | и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.14). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
| и который направлен вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.14). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси.
Угловое ускорение характеризует изменение с течением времени угловой скорости тела. Если за промежуток времени 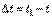 угловая скорость тела изменяется на величину
угловая скорость тела изменяется на величину  , то числовое значение среднего углового ускорения тела за этот промежуток времени будет
, то числовое значение среднего углового ускорения тела за этот промежуток времени будет 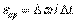 . В пределе при
. В пределе при  найдем,
найдем, 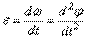 или
или 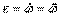 .
.
Таким образом, числовое значение углового ускорения, тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела по времени.
Размерность углового ускорения 1/T2 (1/время2); в качестве единицы измерения обычно применяется рад/с2 или, что то же, 1/с2 (с-2).
Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает, - замедленным. Легко видеть, что вращение будет ускоренным, когда величины  и
и 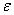 имеют одинаковые знаки, и замедленным, - когда разные.
имеют одинаковые знаки, и замедленным, - когда разные.
Угловое ускорение тела (по аналогии с угловой скоростью) можно также изобразить в виде вектора 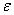 , направленного вдоль оси вращения. При этом
, направленного вдоль оси вращения. При этом 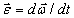 .
.
Направление 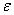 совпадает с направлением
совпадает с направлением  , когда тело вращается ускоренно и (рис.14,а), противоположно
, когда тело вращается ускоренно и (рис.14,а), противоположно  при замедленном вращении (рис.14,б).
при замедленном вращении (рис.14,б).
 1. Скорости точек тела. Рассмотрим какую-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения (см. рис.13). При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время
1. Скорости точек тела. Рассмотрим какую-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения (см. рис.13). При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время 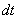 происходит элементарный поворот тела на угол
происходит элементарный поворот тела на угол 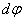 , то точка М при этом совершает вдоль своей траектории элементарное перемещение
, то точка М при этом совершает вдоль своей траектории элементарное перемещение 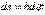 . Тогда числовое значение скорости точки будет равно отношению
. Тогда числовое значение скорости точки будет равно отношению 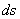 к
к 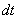 , т.е
, т.е 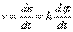 или
или  .
.
Скорость 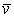 в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.
в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.
Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения.
Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М.
 Так как для всех точек тела
Так как для всех точек тела  имеет в данный момент времени одно и то же значение, то скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.
имеет в данный момент времени одно и то же значение, то скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.
2. Ускорения точек тела. Для нахождения ускорения точки М воспользуемся формулами  ,
, 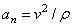 .
.
 В нашем случае
В нашем случае 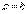 . Подставляя значение
. Подставляя значение 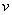 в выражения
в выражения 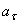 и
и 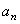 , получим:
, получим: 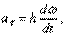
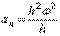 или окончательно:
или окончательно:  ,
, 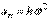 .
.
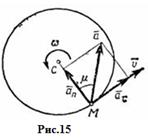
Касательная составляющая ускорения 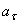 направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при, замедленном); нормальная составляющая
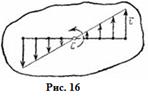
направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при, замедленном); нормальная составляющая 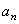 всегда направлена по радиусу МС к оси вращения (рис.16). Полное ускорение точки М будет
всегда направлена по радиусу МС к оси вращения (рис.16). Полное ускорение точки М будет 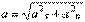 или
или  .
.
 Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом
Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом 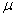 , который вычисляется по формуле
, который вычисляется по формуле 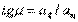 . Подставляя сюда значения
. Подставляя сюда значения 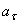 и
и 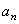 , получаем
, получаем  .
.
Так как  и
и 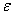 имеют в данный момент времени для всех точек тела одно и то же значение, то ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол
имеют в данный момент времени для всех точек тела одно и то же значение, то ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол 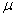 с радиусами описываемых ими окружностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рис.18.
с радиусами описываемых ими окружностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рис.18.
3. Векторы скорости и ускорения точек тела. Чтобы найти выражения непосредственно для векторов 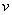 и
и 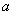 , проведем из произвольной точки О оси АВ радиус-вектор
, проведем из произвольной точки О оси АВ радиус-вектор 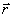 точки М (рис. 17). Тогда
точки М (рис. 17). Тогда 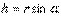 и по формуле
и по формуле
 или
или 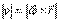 .
.
Таким образом, модуль векторного произведения 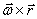 равен модулю скорости точки М. Направления векторов
равен модулю скорости точки М. Направления векторов 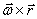 и
и 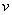 тоже совпадают (оба они перпендикулярны плоскости ОМВ) и размерности их одинаковы. Следовательно,
тоже совпадают (оба они перпендикулярны плоскости ОМВ) и размерности их одинаковы. Следовательно,  - формула Эйлера, т.е. вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки.
- формула Эйлера, т.е. вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки.
Пример 5. Маятник 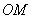 качается в вертикальной плоскости так, что
качается в вертикальной плоскости так, что 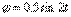 . Длина
. Длина 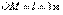 (рис. 19)
(рис. 19)
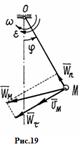 Маятник вращается вокруг горизонтальной оси
Маятник вращается вокруг горизонтальной оси 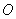 , перпендикулярной вертикальной плоскости. Угловая скорость
, перпендикулярной вертикальной плоскости. Угловая скорость 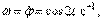 угловое ускорение
угловое ускорение 
Например, при 
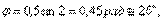
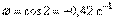 (вращение по часовой стрелке);
(вращение по часовой стрелке);  (угловое ускорение направлено также по часовой стрелке). Вращение в этом положении ускоренное.
(угловое ускорение направлено также по часовой стрелке). Вращение в этом положении ускоренное.
Скорость точки  :
: 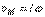
 (определяется модуль скорости). Направлен вектор скорости соответственно направлению угловой скорости – в сторону вращения.
(определяется модуль скорости). Направлен вектор скорости соответственно направлению угловой скорости – в сторону вращения.
Нормальное ускорение 
 касательное ускорение
касательное ускорение 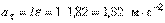 . (Определён опять модуль вектора ускорения. Направлен вектор
. (Определён опять модуль вектора ускорения. Направлен вектор 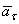 вниз, как указывает угловое ускорение).
вниз, как указывает угловое ускорение).
Величина полного ускорения точки 
2. ППД (что такое? Как представить (в виде двух движений), что такое мгновенный центр скоростей и уметь определять скорости точек и угловые скорости звеньев механизма).
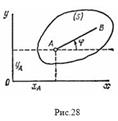 Плоскопараллельным (или плоским) называется такое движение твердого тела, при, котором все его точки перемещаются параллельно некоторой фиксированной плоскости П (рис. 28). Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в кривошипно-ползунном механизме и др. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси.
Плоскопараллельным (или плоским) называется такое движение твердого тела, при, котором все его точки перемещаются параллельно некоторой фиксированной плоскости П (рис. 28). Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в кривошипно-ползунном механизме и др. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси.
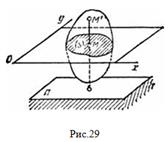
Рассмотрим сечение S тела какой-нибудь плоскости Оxy, параллельной плоскости П (рис.29). При плоскопараллельном движении все точки тела, лежащие на прямой ММ’, перпендикулярной течению S, т. е. плоскости П, движутся тождественно.
Отсюда заключаем, что для изучения движения всего тела достаточно изучить, как движется в плоскости Оху сечение S этого тела или некоторая плоская фигура S. Поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в ее плоскости, т.е. в плоскости Оху.
Положение фигуры S в плоскости Оху определяется положением какого-нибудь проведенного на этой фигуре отрезка АВ (рис. 28). В свою очередь положение отрезка АВ можно определить, зная координаты 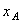 и
и  точки А и угол
точки А и угол  , который отрезок АВ образует с осью х. Точку А, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.
, который отрезок АВ образует с осью х. Точку А, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.
При движении фигуры величины 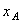 и
и  и
и  будут изменяться. Чтобы знать закон движения, т. е. положение фигуры в плоскости Оху в любой момент времени, надо знать зависимости
будут изменяться. Чтобы знать закон движения, т. е. положение фигуры в плоскости Оху в любой момент времени, надо знать зависимости 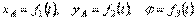 .
.
Уравнения, определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела.
Первые два из уравнений движения определяют то движение, которое фигура совершала бы при  =const; это, очевидно, будет поступательное движение, при котором все точки фигуры движутся так же, как полюс А. Третье уравнение определяет движение, которое фигура совершала бы при
=const; это, очевидно, будет поступательное движение, при котором все точки фигуры движутся так же, как полюс А. Третье уравнение определяет движение, которое фигура совершала бы при  и
и 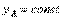 , т.е. когда полюс А неподвижен; это будет вращение фигуры вокруг полюса А. Отсюда можно заключить, что в общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса.
, т.е. когда полюс А неподвижен; это будет вращение фигуры вокруг полюса А. Отсюда можно заключить, что в общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса.
Основными кинематическими характеристиками рассматриваемого движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса 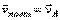 ,
, 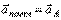 , а также угловая скорость
, а также угловая скорость  и угловое ускорение
и угловое ускорение 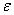 вращательного движения вокруг полюса.
вращательного движения вокруг полюса.
Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю.
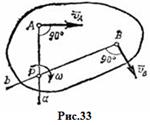 Легко убедиться, что если фигура движется непоступательно, то такая точка в каждый момент времени t существует и притом единственная. Пусть в момент времени t точки А и В плоской фигуры имеют скорости
Легко убедиться, что если фигура движется непоступательно, то такая точка в каждый момент времени t существует и притом единственная. Пусть в момент времени t точки А и В плоской фигуры имеют скорости 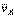 и
и 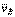 , не параллельные друг другу (рис.33). Тогда точка Р, лежащая на пересечении перпендикуляров Аа к вектору
, не параллельные друг другу (рис.33). Тогда точка Р, лежащая на пересечении перпендикуляров Аа к вектору  и Вb к вектору
и Вb к вектору 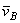 , и будет мгновенным центром скоростей так как
, и будет мгновенным центром скоростей так как  . В самом деле, если допустить, что
. В самом деле, если допустить, что  , то по теореме о проекциях скоростей вектор
, то по теореме о проекциях скоростей вектор 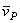 должен быть одновременно перпендикулярен и АР (так как
должен быть одновременно перпендикулярен и АР (так как 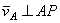 ) и ВР (так как
) и ВР (так как 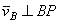 ), что невозможно. Из той же теоремы видно, что никакая другая точка фигуры в этот момент времени не может иметь скорость, равную нулю.
), что невозможно. Из той же теоремы видно, что никакая другая точка фигуры в этот момент времени не может иметь скорость, равную нулю.
Если теперь в момент времени 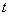 взять точку Р за полюс, то скорость точки А будет
взять точку Р за полюс, то скорость точки А будет  ,
,
так как  . Аналогичный результат получается для любой другой точки фигуры. Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом
. Аналогичный результат получается для любой другой точки фигуры. Следовательно, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей. При этом
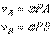
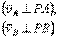 и т.д.
и т.д.
Из равенств, следует еще, что
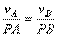
т.е. что скорости точек плоской фигуры пропорциональны их расстояниям от МЦС.
Полученные результаты приводят к следующим выводам.
1. Для определения мгновенного центра скоростей надо знать только направления скоростей 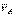 и
и 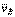 каких-нибудь двух точек А и В плоской фигуры (или траектории этих точек); мгновенный центр скоростей находится в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек (или к касательным к траекториям).
каких-нибудь двух точек А и В плоской фигуры (или траектории этих точек); мгновенный центр скоростей находится в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек (или к касательным к траекториям).
2. Для определения скорости любой точки плоской фигуры, надо знать модуль и направление скорости какой-нибудь одной точки А фигуры и направление скорости другой ее точки В. Тогда, восставив из точек А и В перпендикуляры к  и
и 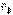 , построим мгновенный центр скоростей Р и по направлению
, построим мгновенный центр скоростей Р и по направлению 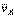 определим направление поворота фигуры. После этого, зная
определим направление поворота фигуры. После этого, зная  , найдем скорость
, найдем скорость 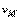 любой точки М плоской фигуры. Направлен вектор
любой точки М плоской фигуры. Направлен вектор 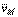 перпендикулярно РМ в сторону поворота фигуры.
перпендикулярно РМ в сторону поворота фигуры.
3. Угловая скорость  плоской фигуры равна в каждый данный момент времени отношению скорости какой-нибудь точки фигуры к ее расстоянию от мгновенного центра скоростей Р:
плоской фигуры равна в каждый данный момент времени отношению скорости какой-нибудь точки фигуры к ее расстоянию от мгновенного центра скоростей Р: 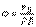 .
.
 Рассмотрим некоторые частные случаи определения мгновенного центра скоростей.
Рассмотрим некоторые частные случаи определения мгновенного центра скоростей.
а) Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого неподвижного, то точка Р катящегося тела, касающаяся неподвижной поверхности (рис.34), имеет в данный момент времени вследствие отсутствия скольжения скорость, равную нулю ( ), и, следовательно, является мгновенным центром скоростей. Примером служит качение колеса по рельсу.
), и, следовательно, является мгновенным центром скоростей. Примером служит качение колеса по рельсу.
 б) Если скорости точек А и В плоской фигуры параллельны друг другу, причем линия АВ не перпендикулярна
б) Если скорости точек А и В плоской фигуры параллельны друг другу, причем линия АВ не перпендикулярна  (рис.35,а), то мгновенный центр скоростей лежит в бесконечности и скорости всех точек параллельны
(рис.35,а), то мгновенный центр скоростей лежит в бесконечности и скорости всех точек параллельны  . При этом из теоремы о проекциях скоростей следует, что
. При этом из теоремы о проекциях скоростей следует, что  т. е.
т. е.  ; аналогичный результат получается для всех других точек. Следовательно, в рассматриваемом случае скорости всех точек фигуры в данный момент времени равны друг другу и по модулю, и по направлению, т.е. фигура имеет мгновенное поступательное распределение скоростей (такое состояние движения тела называют еще мгновенно поступательным). Угловая скорость
; аналогичный результат получается для всех других точек. Следовательно, в рассматриваемом случае скорости всех точек фигуры в данный момент времени равны друг другу и по модулю, и по направлению, т.е. фигура имеет мгновенное поступательное распределение скоростей (такое состояние движения тела называют еще мгновенно поступательным). Угловая скорость  тела в этот момент времени, как видно равна нулю.
тела в этот момент времени, как видно равна нулю.
в) Если скорости точек А и В плоской фигуры параллельны друг другу и при этом линия АВ перпендикулярна  , то мгновенный центр скоростей Р определяется построением, показанным на рис. 35,б. Справедливость построений следует из пропорции. В этом случае, в отличие от предыдущих, для нахождения центра Р надо кроме направлений знать еще и модули скоростей
, то мгновенный центр скоростей Р определяется построением, показанным на рис. 35,б. Справедливость построений следует из пропорции. В этом случае, в отличие от предыдущих, для нахождения центра Р надо кроме направлений знать еще и модули скоростей  и
и  .
.
г) Если известны вектор скорости 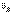 какой-нибудь точки В фигуры и ее угловая скорость
какой-нибудь точки В фигуры и ее угловая скорость  , то положение мгновенного центра скоростей Р, лежащего на перпендикуляре к
, то положение мгновенного центра скоростей Р, лежащего на перпендикуляре к  (рис.35,б), можно найти как
(рис.35,б), можно найти как  .
.
Решение задач на определение скорости.
Для определения искомых кинематических характеристик (угловой скорости тела или скоростей его точек) надо знать модуль и направление скорости какой-нибудь одной точки и направление скорости другой точки сечения этого тела. С определения этих характеристик по данным задачи и следует начинать решение.
Механизм, движение которого исследуется, надо изображать на чертеже в том положении, для которого требуется определить соответствующие характеристики. При расчете следует помнить, что понятие о мгновенном центре скоростей имеет место для данного твердого тела. В механизме, состоящем из нескольких тел, каждое непоступательное движущееся тело имеет в данный момент времени свой мгновенный центр скоростей Р и свою угловую скорость.
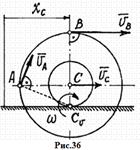 Пример 8. Тело, имеющее форму катушки, катится своим средним цилиндром по неподвижной плоскости так, что
Пример 8. Тело, имеющее форму катушки, катится своим средним цилиндром по неподвижной плоскости так, что 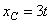 (см). Радиусы цилиндров: R = 4 см и r = 2 см (рис.36)..
(см). Радиусы цилиндров: R = 4 см и r = 2 см (рис.36)..
Определим скорости точек А,В и С.
Мгновенный центр скоростей находится в точке касания катушки с плоскостью.
Скорость полюса С  .
.
|
Угловая скорость катушки 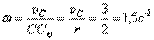 .
.
Скорости точек А и В направлены перпендикулярно отрезкам прямых, соединяющих эти точки с мгновенным центром скоростей. Величина скоростей:
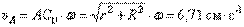 ,
, 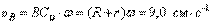
Пример 9. Стержень АВ скользит концами по взаимно перпендикулярным прямым так, что при угле 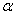 скорость
скорость 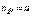 . Длина стержня
. Длина стержня 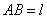 . Определим скорость конца А и угловую скорость стержня.
. Определим скорость конца А и угловую скорость стержня.
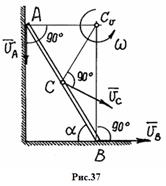
Нетрудно определить направление вектора скорости точки А, скользящей по вертикальной прямой. Тогда 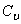 находится на пересечении перпендикуляров к
находится на пересечении перпендикуляров к 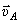 и
и  (рис. 37).
(рис. 37).
Угловая скорость 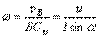 .
.
Скорость точки А:  .
.
|
А скорость центра стержня С, например, направлена перпендикулярно 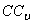 и равна:
и равна: 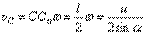 .
.
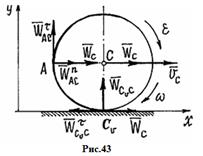 Пример 11. Диск катится без скольжения по прямой. Центр его С имеет скорость
Пример 11. Диск катится без скольжения по прямой. Центр его С имеет скорость 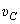 и ускорение
и ускорение 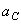 (рис. 43). Найдем ускорение точки А.
(рис. 43). Найдем ускорение точки А.
Угловую скорость находим с помощью мгновенного центра скоростей:
|
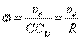 .
.
Угловое ускорение при таком движении можно найти как производную от угловой скорости. Имея в виду, что 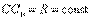 , а точка С движется по прямой, получим
, а точка С движется по прямой, получим
 .
.
Если С – полюс, то 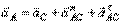 , где
, где 
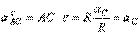 .
.
Величину ускорения найдём с помощью проекций на оси х и у: 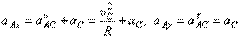
|
Тогда  .
.
Ускорение мгновенного центра скоростей 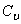 :
:  , где
, где 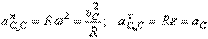 .
.
И, так как  , ускорение
, ускорение  и
и 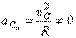 .
.
Таким образом, ускорение мгновенного центра скоростей не равно нулю.
3. Сложное движение точки (где такое движение? Уметь определять величину и направление скорости).
Date: 2015-09-03; view: 677; Нарушение авторских прав