Определение скоростей точек тела

Воспользуемся векторным способом задания движения для нахождения скорости произвольной точки M. Из (рис. 2.23) имеем

.

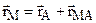Для определения скорости точки M вычислим векторную производную от вектора :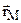

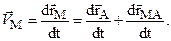
Очевидно , а определяет скорость точки M от вращения сечения (S) вокруг полюса. Тогда

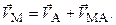
(2.30)

Уравнение (2.30) выражает следующую теорему: скорость любой точки тела при плоском его движении равна геометрической сумме скорости полюса от поступательного движения тела и скорости точки от вращения тела вокруг полюса.

Скорость 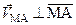, а ее модуль .

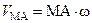Пример 2.10. Определить скорость точки B тела, совершающего плоское движение, если известны скорость полюса 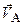, угловая скорость 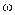и расстояние AB.

В соответствии с(2.30) имеем 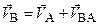; вычислив 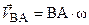и принимая во внимание, что построением параллелограмма находим 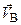(рис. 2.24).

Теорема: Если тело совершает плоское движение, то проекции скоростей двух любых точек тела на прямую их соединяющую, равны по величине и имеют одинаковое направление.

Найдем скорость точки B по известным данным 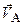, , 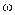AB (рис. 2.25):

.

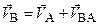Спроектируем данное равенство на прямую AB:

или 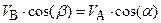, что и требовалось доказать.

Date: 2015-09-03; view: 340; Нарушение авторских прав