Координатное представление скалярного произведения

Полезным инструментом исследования свойств набора элементов 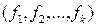в евклидовом пространстве является матрица Грамма.

Определение 15.5 В евклидовом пространстве E матрицей Грамма системы элементов 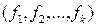называется симметрическая матрица вида

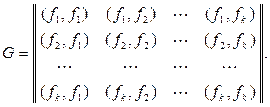
Пусть в E дан базис 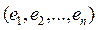. Скалярное произведение элементов 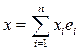и представляется в виде

,

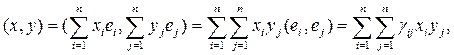где – компоненты матрицы , называемой базисной матрицей Грамма.

Замечание. Э та матрица симметрическая, в силу коммутативности скалярного произведения и является матрицей симметричного билинейного функционала, задающего скалярное произведение. Тогда координатное представление скалярного произведения можно записать так:

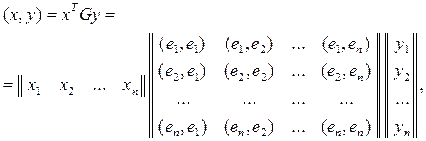
где 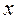и 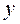– координатные представления (столбцы) элементов x и y в базисе .

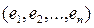Замечание. В ортонормированном базисе 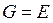, и, следовательно, формула для скалярного произведения принимает вид

.

Теорема 15.3 Для базисной матрицы Грамма 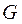в любом базисе .

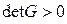Доказательство.

Из определения 15.1 следует, что скалярное произведение есть билинейный, симметричный функционал, поэтому при переходе от базиса 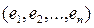к базису 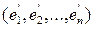(с матрицей перехода 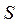) по теореме 14.4 (лекция 14) для матрицы Грамма имеют место равенства

где ,

откуда следует, что значение 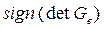инвариантно, то есть не изменяется при замене базиса. Принимая во внимание, что в ортонормированном базисе 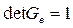, приходим к заключению, что в любом базисе

Теорема доказана.

Следствие. Система элементов в 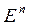линейно независима тогда и только тогда, когда определитель матрицы Грамма этой системы положителен.

Доказательство.

Если элементы 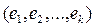линейно зависимы, то определитель их матрицы Грамма равен нулю. Действительно, пусть существуют не равные нулю одновременно числа , такие, что

.

Умножив это равенство скалярно слева на , получим

.

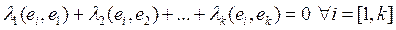Эти соотношения можно рассматривать как систему линейных уравнений относительно коэффициентов 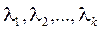. Эта система имеет нетривиальное решение только в случае, когда равен нулю главный определитель системы а, следовательно, будет равен нулю определитель матрицы Грамма.

С другой стороны, если элементы 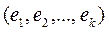линейно независимы, то они образуют базис в своей линейной оболочке и к ним применим результат теоремы 15.3.

Следствие доказано.

Теорема 15.4 (критерий Сильвестра) Для положительной определенности квадратичного функционала в необходимо и достаточно, чтобы все главные миноры его матрицы, имеющие вид

,

были положительными.

Date: 2015-09-03; view: 555; Нарушение авторских прав