
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Если при и неравенство (1) выполняется как строгое, то функция называется строго выпуклой
|
|
Выпуклые функции
Определение 1. Функция, определенная на, называется выпуклой, если для любых и любого выполняется неравенство
 . (1)
. (1)
Если при и неравенство (1) выполняется как строгое, то функция называется строго выпуклой.
Определение 2. Функция 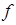 , определенная на
, определенная на 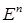 , называется вогнутой (строго вогнутой), если функция
, называется вогнутой (строго вогнутой), если функция  является выпуклой (строго выпуклой).
является выпуклой (строго выпуклой).
Очевидно, что любая строго выпуклая (строго вогнутая) функция является выпуклой (вогнутой) функцией, но не наоборот.
Приведем некоторые операции допустимые в классе выпуклых функций.
Теорема 1. Пусть все функции  ,
,  ,
,
выпуклы на 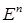 , числа
, числа 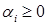 . Тогда функция
. Тогда функция  также выпукла.
также выпукла.
Доказательство. Пусть заданы векторы  и число
и число 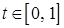 . Так как функции
. Так как функции 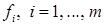 , выпуклы, то для всех
, выпуклы, то для всех 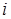 выполняются неравенства
выполняются неравенства
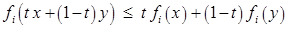 . Умножая эти неравенства на неотрицательные величины
. Умножая эти неравенства на неотрицательные величины 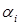 и суммируя их по
и суммируя их по 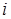 , получим неравенство
, получим неравенство
 .
.
Следовательно, 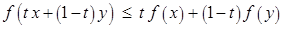 . Что и требовалось.
. Что и требовалось.
Теорема 2. Пусть на 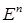 определены функции
определены функции
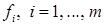 ,
,  . Если все
. Если все  – выпуклые, то функция
– выпуклые, то функция 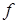 также выпуклая.
также выпуклая.
Доказательство. Пусть заданы векторы 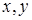 и число
и число 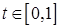 . Так как функции
. Так как функции  выпуклы, то для всех
выпуклы, то для всех 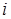 выполняются неравенства
выполняются неравенства
 . Следовательно,
. Следовательно,

для всех 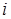 . Из полученных неравенств имеем
. Из полученных неравенств имеем
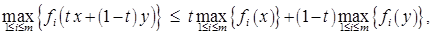
то есть  . Что и требовалось.
. Что и требовалось.
Приведем теоремы о суперпозициях выпуклых функций.
Теорема 3. Пусть функция 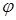 определена на отрезке
определена на отрезке 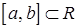 и является на нем выпуклой и неубывающей; функция
и является на нем выпуклой и неубывающей; функция 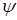 выпукла на выпуклом множестве
выпукла на выпуклом множестве 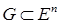 ,
,  ,
,  для всех
для всех  . Тогда функция
. Тогда функция 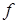 выпукла на
выпукла на  .
.
Доказательство. Пусть 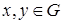 ,
,  . Тогда
. Тогда  в силу выпуклости функции
в силу выпуклости функции 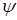 на
на  . Очевидно, что
. Очевидно, что 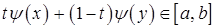 . Поэтому, а также в силу монотонности и выпуклости
. Поэтому, а также в силу монотонности и выпуклости 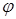 на
на  , имеем
, имеем

Следовательно, 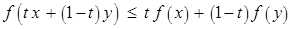 . Что и требовалось.
. Что и требовалось.
Теорема 4. Пусть 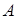 – матрица размерности
– матрица размерности  ,
, 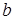 – вектор размерности
– вектор размерности  ,
, 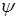 – функция, определенная и выпуклая на многообразии
– функция, определенная и выпуклая на многообразии
 ,
, 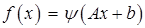 . Тогда функция
. Тогда функция 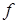 выпукла на
выпукла на 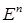 .
.
Доказательство. Пусть заданы векторы  и число
и число 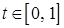 . Тогда имеем
. Тогда имеем
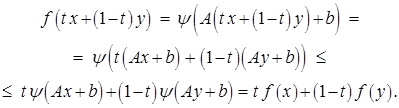
Что и требовалось.
Далее покажем, что выпуклость функции многих переменных можно установить, исследуя на выпуклость ее сужения на всевозможные прямые в 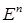 . Выпуклость функции одной переменной установить зачастую значительно проще, чем выпуклость функции многих переменных.
. Выпуклость функции одной переменной установить зачастую значительно проще, чем выпуклость функции многих переменных.
Пусть заданы функция 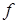 и векторы
и векторы 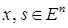 . Сужение
. Сужение 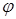 функции
функции 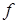 на прямую
на прямую  определим следующим образом:
определим следующим образом:
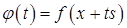 . (2)
. (2)
Теорема 5. Функция 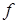 является выпуклой тогда и только тогда, когда выпуклой является и функция
является выпуклой тогда и только тогда, когда выпуклой является и функция 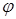 , определенная по формуле (2) при любых
, определенная по формуле (2) при любых 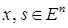 .
.
Доказательство. Необходимость. Пусть 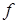 –
–
выпуклая функция, 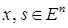 . Покажем, что функция
. Покажем, что функция 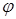 также является выпуклой. Пусть
также является выпуклой. Пусть  . Тогда
. Тогда 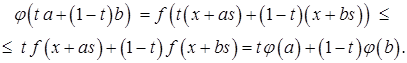
Достаточность. Предположим, что для произвольных 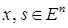 функция
функция 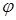 – выпуклая. Пусть
– выпуклая. Пусть  и
и 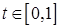 . Тогда
. Тогда

Что и требовалось.
Далее установим связь между выпуклыми множествами и выпуклыми функциями.
Пусть  – некоторая константа. Множество
– некоторая константа. Множество 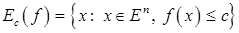 называется лебеговым множеством функции
называется лебеговым множеством функции 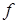 .
.
Теорема 6. Пусть функция 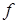 выпукла на
выпукла на 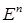 . Тогда любое ее лебегово множество выпукло.
. Тогда любое ее лебегово множество выпукло.
Доказательство. Пусть 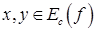 ,
, 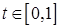 . Тогда из
. Тогда из 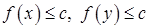 и в силу выпуклости
и в силу выпуклости 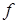
 . Таким
. Таким
образом,  , что и означает выпуклость множества
, что и означает выпуклость множества  .
.
Эта теорема устанавливает одностороннюю связь между выпуклыми множествами и выпуклыми
функциями. Утверждение, обратное теореме 6, не имеет места.
| <== предыдущая | | | следующая ==> |
| По вопросам предоставления коммунальных услуг | | | Вычерчивание масштабных условных знаков |
Date: 2015-09-02; view: 542; Нарушение авторских прав