
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

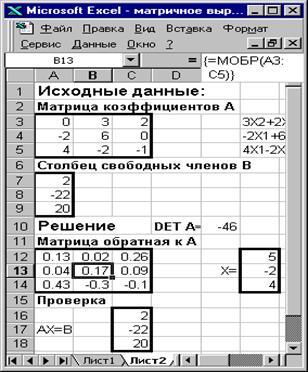
Пример №2. Решить систему линейных уравнений в матричном виде, сделать проверку решения
|
|
 Решение:
Решение:
1. Поместим исходные данные – матрицу коэффициентов А и столбец свободных членов уравнений В - в ячейки A3:C5 и A7:A9 соответственно.
2. С помощью функции МОПРЕД проверим определитель матрицы А. Если он не равен 0, то существует матрица, обратная к А.
3. Найдем матрицу, обратную к А, для этого:
· Выделим интервал ячеек, например А12:C14
· С помощью команды меню 4Вставка 4Функции открываем диалоговое окно мастера функций, выбираем в окне Категория –Математические, в окне Функция – МОБР, нажимаем на кнопку ОК
· В окне для аргумента функции набираем А3:С5
· После нажатия на кнопку ОК помещаем курсор в строку формул и одновременно нажимаем клавиши Crtl +Shift+Enter.
4. Найдем решение уравнения в виде вектора Х, для этого с помощью функции МУМНОЖ перемножим матрицу, обратную к А и вектор-столбец В.
5. Выполним проверку и убедимся, что найденный вектор Х удовлетворяет исходной системе уравнений АХ=В.
.
Варианты заданий
| Номер варианта | Матричное выражение | Система линейных уравнений |
| ((QT34+D43)H32)T=? | X1-2X2+6X3=-28 3X1 +3X3=-6 -2X1+X2-4X3=15 | |
| (BT23+H32)(E22+D22)=? | 2X1 +X3=6 4X1-3X2-2X3=-1 2X2+7X3=12 | |
| (QT34D34+E44)T=? | -3x1+2x3=5 2x1+4x2+4x3=-2 x1-2x2+5x3=31 | |
| (E33+H33+DT33)Q34=? | 3x2+2x3=2 -2x1+6x2=-22 4x1-2x2-x3=20 | |
| ((E44+DT44)(Q43-B43))T=? | 5x1+2x2+x3=21 -2x1-4x2+2x3=-2 7x2+8x3=-14 | |
| ((H34B43)T+E33-D33)T=? | 6x1-2x2=18 4x1+3x2+4x3=-1 6x2+x3=-18 | |
| ((D34+B34)Q43)T+E33=? | 8x2+9x3=38 2x1+4x2-2x3=-14 -3x1+2x2+x3=-7 | |
| (DT34(E33+B33+H33))T=? | 2x1+4x2+x3=2 -x1+6x2+8x3=17 3x2-12x3=-54 | |
| D43(E33+H33)T+QT34=? | -x2-4x3=-18 -8x1+2x2+2x3=12 4x1+4x2=8 | |
| (D33+E33)T+H34Q43=? | 7x1+6x2+8x3=64 2x1+3x2-5x3=-19 4x1+5x2+2x3=29 | |
| (Q34BT34+E33-D33)T=? | 9x1+7x2-x3=39 -3x2+4x3=-9 3x1+x2+9x3=9 | |
| (E33+D33)T(Q34B43)=? | 5x1+x3=25 6x1+7x2+10x3=81 -2x1+4x2+x3=1 | |
| (D43+HT34)(E33+Q33)T=? | -x1+8x2-3x3=1 8x1+2x2=-38 -5x2=7x3=-34 | |
| (((E44+Q44)D42)H23)T=? | -6x1+7x2-4=-44 3x1+6x2+6x3=57 5x1+4x2+7x3=71 | |
| ((E33+H33)T+B33)D32=? | -x1-7x2+6x3=-14 2x1+5x2+2x3=19 9x1+6x2+6x3=69 |
Date: 2015-09-02; view: 552; Нарушение авторских прав