Уравнения равновесия покоящейся жидкости

Для вывода уравнений равновесия выделим в покоящейся жидкости бесконечно малый прямоугольный параллелепипед с ребрами dx, dy, dz (рис. 2.3).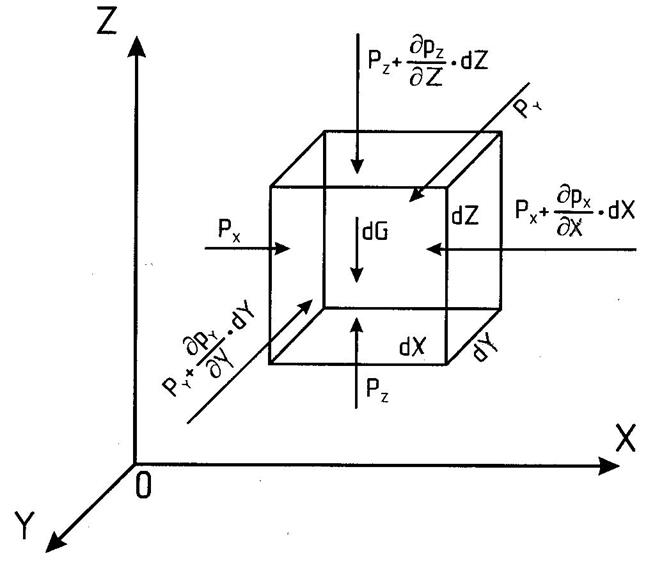

Рис. 2.3

На параллелепипед действуют силы гидростатического давления и массовые силы.

На грани площадью dydz будут действовать средние гидростатические давления px и px+ 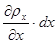, где 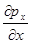– частная производная pxпо x, характеризующая изменение давления в направлении оси x, т.е. его приращение. На другие грани средние гидростатические давления действуют по аналогии с показанным.

Равнодействующую массовых сил обозначим G, а ее проекции на координатные оси,

отнесенные к единице массы, обозначим X, Y, Z (X = Gx/m; Y = Gy/m; Z = Gz/m). dW = dxdydz; m = 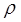dW.

Сумма проекций всех сил на соответствующие оси координат имеет вид: на ось x

;

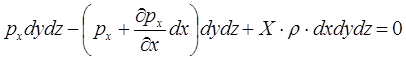на ось y ;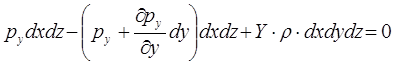

на ось z .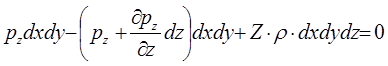

Выполним преобразования в этих уравнениях (раскроем скобки, сократим общие члены, а оставшиеся разделим на величину ).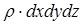

;

;

.

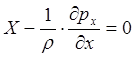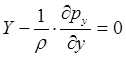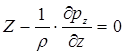Получили уравнения равновесия жидкости (уравнения Эйлера, выведены в 1755 году), которые в дифференциальной форме выражают зависимость между силами, действующими на жидкость, и координатами любой ее точки.

Date: 2015-09-02; view: 667; Нарушение авторских прав