
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Умножение матриц
|
|
Определение 14.4 Произведением матрицы  размеров
размеров  на матрицу
на матрицу 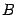 размеров
размеров  называется матрица
называется матрица 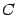 размеров
размеров 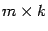 , элементы которой вычисляются по формуле
, элементы которой вычисляются по формуле
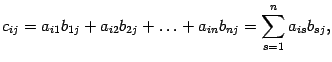
| (14.5) |
где 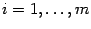 ,
,  .
.
Во-первых, в этом определении нужно обратить внимание на то, что важен порядок сомножителей, нужно знать, какой сомножитель первый, а какой -- второй.
Во-вторых, нужно отметить, что произведение определено только в том случае, если число столбцов первого сомножителя равно числу строк второго. Если это условие не выполняется, то произведение не определено.
В-третьих, размеры результата умножения определяются следующим образом: число строк результата равно числу строк первого сомножителя, а число столбцов результата равно числу столбцов второго сомножителя.
Правило вычисления элементов произведения можно сформулировать следующим образом.
Для того, чтобы вычислить элемент произведения, стоящий в 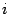 -ой строке и
-ой строке и  -ом столбце, нужно взять
-ом столбце, нужно взять 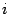 -ую строку первого сомножителя и
-ую строку первого сомножителя и  -ый столбец второго сомножителя, попарно перемножить их элементы, стоящие на одинаковых местах, и результаты сложить. (Точно так же мы поступаем, когда находим скалярное произведение двух векторов по их координатам, см. формулу (14.2).)
-ый столбец второго сомножителя, попарно перемножить их элементы, стоящие на одинаковых местах, и результаты сложить. (Точно так же мы поступаем, когда находим скалярное произведение двух векторов по их координатам, см. формулу (14.2).)
Пример 14.3 Даны матрицы 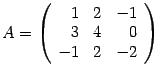 ,
, 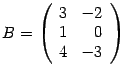 . Найдите произведения
. Найдите произведения 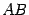 и
и 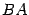 .
.
Решение. Рассмотрим произведение 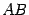 . Число столбцов в первом сомножителе
. Число столбцов в первом сомножителе 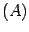 равно 3, число строк во втором сомножителе
равно 3, число строк во втором сомножителе 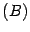 тоже равно 3. Числа совпали, следовательно, произведение определено.
тоже равно 3. Числа совпали, следовательно, произведение определено.
Результатом умножения будет матрица 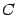 ,
,  , у которой строк столько, сколько их в первом сомножителе, то есть 3, а столбцов столько, сколько их во втором сомножителе, то есть 2. Итак, матрица
, у которой строк столько, сколько их в первом сомножителе, то есть 3, а столбцов столько, сколько их во втором сомножителе, то есть 2. Итак, матрица 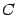 имеет размеры
имеет размеры 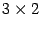 .
.
Находим элемент  . В его вычислении участвует первая строка
. В его вычислении участвует первая строка 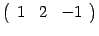 первого сомножителя
первого сомножителя 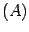 и первый столбец
и первый столбец 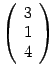 второго сомножителя
второго сомножителя 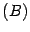 :
:
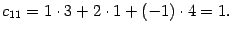
Находим элемент 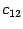 . В его вычислении участвует первая строка
. В его вычислении участвует первая строка 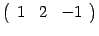 первого сомножителя
первого сомножителя 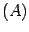 и второй столбец
и второй столбец  второго сомножителя
второго сомножителя 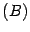 :
:
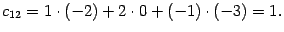
Все элементы первой строки матрицы 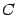 вычислены. Находим элемент
вычислены. Находим элемент 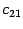 . В его вычислении участвует вторая строка
. В его вычислении участвует вторая строка 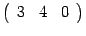 первого сомножителя
первого сомножителя 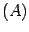 и первый столбец
и первый столбец 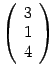 второго сомножителя
второго сомножителя 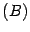 :
:
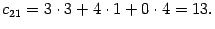
Находим элемент 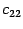 . В его вычислении участвует вторая строка
. В его вычислении участвует вторая строка 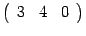 первого сомножителя
первого сомножителя 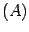 и второй столбец
и второй столбец  второго сомножителя
второго сомножителя 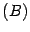 :
:

Вычислены все элементы второй строки матрицы 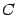 . Аналогично находим элементы третьей строки:
. Аналогично находим элементы третьей строки:


Итак,  .
.
Рассмотрим произведение 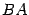 . Число столбцов в первом сомножителе
. Число столбцов в первом сомножителе 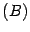 равно 2, число строк во втором сомножителе
равно 2, число строк во втором сомножителе 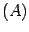 равно 3. Числа не совпали, следовательно, произведение не определено.
равно 3. Числа не совпали, следовательно, произведение не определено.
Ответ:  , произведение
, произведение 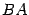 не определено.
не определено.
Замечание 14.3 Легко проверить, что произведение квадратных матриц одного порядка всегда существует (определено).
У читателя может возникнуть законный вопрос: "Зачем так сложно определять произведение матриц? Нельзя ли его определить попроще, например, как произведение элементов матриц-сомножителей, стоящих на одинаковых местах?" Ответ на этот вопрос мы увидим позже, когда будем рассматривать системы линейных уравнений, правило изменения координат векторов при изменении базиса и такие неизвестные пока читателю объекты как линейные преобразования и квадратичные формы. Тогда мы увидим, что введенное определение умножения матриц используется очень эффективно, что оно "похоже" на умножение чисел. Если же произведение матриц определить по-другому, то его не удается разумно использовать ни в математике, ни в прикладных науках.
Рассмотрим, какими свойствами обладает операция умножения матриц.
Прежде всего отметим, что умножение матриц -- некоммутативная операция. Это означает, что существуют такие матрицы  и
и 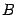 , что
, что
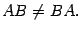
Для прямоугольных матриц мы убедились в этом в примере 14.3. В нем произведение 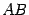 существует, а произведение
существует, а произведение 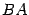 -- нет. Для квадратных матриц это видно из следующего примера. Пусть
-- нет. Для квадратных матриц это видно из следующего примера. Пусть 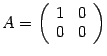 ,
, 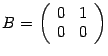 . Тогда
. Тогда
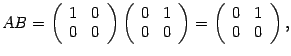

то есть 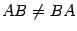 .
.
Предложение 14.4 Умножение матриц обладает следующими свойствами: 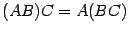 -- ассоциативность умножения;
-- ассоциативность умножения; 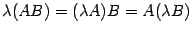 , где
, где  -- число;
-- число; 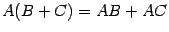 ,
,  -- дистрибутивность умножения;
-- дистрибутивность умножения; 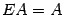 ,
, 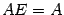 , где
, где  -- единичная матрица соответствующего порядка. Предполагается, что все указанные произведения имеют смысл.
-- единичная матрица соответствующего порядка. Предполагается, что все указанные произведения имеют смысл.
Доказательство. На протяжении всего доказательства предполагается, что  -- матрица размеров
-- матрица размеров  .
.
Докажем свойство ассоциативности. Чтобы произведение 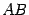 было определено, матрица
было определено, матрица 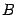 должна иметь размеры
должна иметь размеры  . Произведение
. Произведение 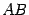 обозначим буквой
обозначим буквой  . Тогда матрица
. Тогда матрица  имеет размеры
имеет размеры 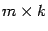 . Чтобы произведение
. Чтобы произведение 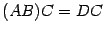 было определено, матрица
было определено, матрица 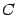 должна иметь размеры
должна иметь размеры  . Матрицу
. Матрицу 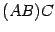 обозначим
обозначим  , матрицу
, матрицу  обозначим
обозначим 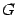 , матрицу
, матрицу 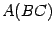 обозначим
обозначим  . Покажем, что элементы, стоящие в
. Покажем, что элементы, стоящие в 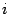 -ой строке и
-ой строке и  -ом столбце матриц
-ом столбце матриц  и
и  , равны друг другу, то есть что
, равны друг другу, то есть что 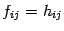 .
.
По определению

Подставив 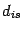 из второго равенства в первое, получим
из второго равенства в первое, получим
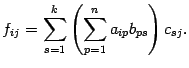
В силу предложения 14.1
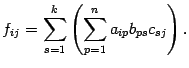
В силу предложения 14.3
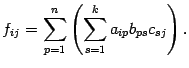
| (14.6) |
С другой стороны
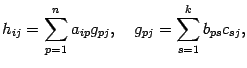
откуда

Применим предложение 14.1
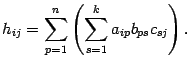
Сравнивая этот результат с (14.6), заключаем, что 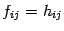 . Ассоциативность умножения доказана.
. Ассоциативность умножения доказана.
Свойство 2 предоставляем читателю доказать самостоятельно.
Докажем дистрибутивность умножения. Чтобы произведение 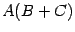 было определено, матрицы
было определено, матрицы 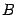 и
и 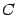 должны иметь размеры
должны иметь размеры  . Положим
. Положим 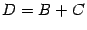 ,
, 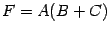 ,
, 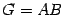 ,
, 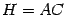 ,
, 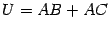 . Для доказательства равенства
. Для доказательства равенства 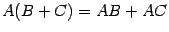 , нужно доказать, что
, нужно доказать, что 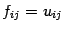 ,
, 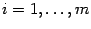 ,
,  .
.
Так как 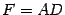 , то
, то
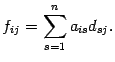
По определению суммы матриц,  . Следовательно,
. Следовательно,
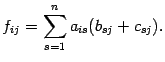
| (14.7) |
С другой стороны,

Тогда

Сравнивая полученный результат с (14.7), получаем 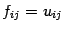 . Первое равенство в свойстве дистрибутивности доказано. Второе равенство доказывается аналогично.
. Первое равенство в свойстве дистрибутивности доказано. Второе равенство доказывается аналогично.
Докажем первое равенство в свойстве 4. Чтобы произведение 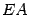 было определено, матрица
было определено, матрица  должна иметь порядок
должна иметь порядок 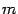 . Пусть
. Пусть 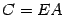 . Тогда
. Тогда
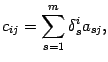
где  -- символ Кронекера. Сумма справа имеет вид
-- символ Кронекера. Сумма справа имеет вид
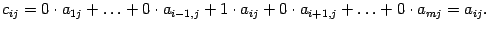
Таким образом 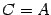 , первое равенство в свойстве 4 доказано. Второе равенство доказывается аналогично.
, первое равенство в свойстве 4 доказано. Второе равенство доказывается аналогично.
Замечание 14.4 Из ассоциативности умножения матриц следует, что если произведение содержит три и более сомножителей, то его можно записывать без использования скобок. Например, 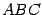 или
или  . Эта кажущаяся очевидной запись произведения верна не для всяких математических объектов. Действительно, в силу предложения 10.23, для векторного произведения векторов запись
. Эта кажущаяся очевидной запись произведения верна не для всяких математических объектов. Действительно, в силу предложения 10.23, для векторного произведения векторов запись  неприемлема, так как результат вычисления этого произведения зависит от расстановки скобок.
неприемлема, так как результат вычисления этого произведения зависит от расстановки скобок.
Замечание 14.5 Свойство дистрибутивности позволяет раскрывать скобки в матричных выражениях. Но нужно обратить внимание, что, раскрывая скобки, нельзя менять порядок сомножителей.
Замечание 14.6 Свойство 4 объясняет происхождение названия "единичная" матрица. В умножении матриц единичная матрица ведет себя так же, как число 1 при умножении чисел.
| <== предыдущая | | | следующая ==> |
| Правила оформления дипломной выпускной квалификационной работы | | | Политика ускорения |
Date: 2015-09-02; view: 398; Нарушение авторских прав