
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоретические сведения
|
|
Выполнение сетей петри
ЦЕЛЬ РАБОТЫ
15.1.1 Ознакомиться с теоретическими сведениями.
15.1.2 Получить практические навыки по выполнению сетей Петри.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
15.2.1 Методические указания по выполнению практической работы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
15.3.1 Изучить методические указания к практической работе.
15.3.2 В соответствии с полученным вариантом выполните сеть Петри.
15.3.3 В соответствии с полученным вариантом описать свойства сети Петри
СОДЕРЖАНИЕ ОТЧЕТА
15.4.1 Цель работы
15.4.2 Методические рекомендации
15.4.3 Порядок выполнения работы
15.4.4 Ответы на контрольные вопросы
15.4.5 Выводы
КОНТРОЛЬНЫЕ ВОПРОСЫ
15.5.1 Что называется сетью Петри?
15.5.2 Назовите статистические свойства сети Петри?
15.5.3 Назовите динамические свойства сети Петри?
15.5.4 Что называется маркировкой сети Петри?
15.5.5 Какой переход маркированной сети Петри называется разрешенным?
ПРИЛОЖЕНИЕ 1
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
В связи со все более широким использованием параллельных и распределенных вычислительных систем особую актуальность приобретают дискретные структуры, представляющие параллельные процессы. Аппаратом описания сложных систем взаимодействующих процессов являются формальные системы типа сетей Петри, моделирующие динамические свойства систем.
Формализм сетей Петри общего вида основан на понятии комплекта, являющемся в некотором роде обобщением понятия множества. Как и множество, комплект – это набор элементов, но всякий элемент и множества, заменяются на функцию числа экземпляров элемента в комплекте, которая обозначается как #(x, B) (читается: «число х в комплекте В»). Множество – частный случай комплекта.
Многие понятия теорий множества распространяются и на комплект. Так, пустой комплект аналогичен пустому множеству. Мощность комплекта есть общее число экземпляров элементов в комплекте. Комплект А включен в комплект В (является под комплектом), если для всякого x#(x, A)£#(x, B). С помощью функции # легко определяются операции над комплектами: для объединения комплектов А и В #(x, AÈB) = max (#(x, A), #(x, B)); для пересечения комплектов А и В #(x, AÇB) = min (#(x, A), #(x, B)); для сумм комплектов А и В #(x, A+B) = #(x, A)+#(x, B); для разности комплектов А и В #(x, A-B) = #(x, A)-#(x, AÇB). Если М – множество, то M¢¢ - множество всех комплектов, построенных из элементов М, что #(x, B)£n, BÎMn; M¥ - множество всех комплектов, построенных из элементов М без ограничения на число экземпляров элемента в комплекте.
Сети Петри – это четверка C=(P, T, I, O), где З – конечное множество позиций, Т – конечное множество переходов, I: Т®Р¥ - входная функция, отображающая переходы в комплекты позиций, О: Т®Р¥ - выходная функция, отображающая переходы в комплекты позиций. Графически сеть Петри изображаются в виде мультиграфа с вершинами двух видов: кружки соответствуют позициям, планки – переходам. Функции I и О представляются дугами (рис.1).
Позиции, дуги из которых ведут в переход tj, называются выходными для tj; аналогично, позиции, в которые ведут дуги из перехода tj, называются выходными для tj. Множество входных позиций обозначают I(tj), а выходные – O(tj). В сети Петри, изображенной на рис.1, I(t1)={p1, p1, p1}, O(t1)={p3, p4, p4}. Функции I и О удобно обобщить на отображение из позиций в комплекты переходов (Р®Т¥), что позволяет обозначать множества входных и выходных переходов позиции pi, определяемые аналогично множествам входных и выходных позиций перехода, соответственно как I(pi) и O(pi). В сети Петри, изображенной на рис. 1, I(p3)={t1, t2}, O(p3)={t2, t4}.
Введенные понятия относятся к статистической структуре сети Петри. Динамические свойства сети Петри определяются с помощью понятия маркировки. Маркировка m сети Петри C=(P, T, I, O) – это функция, отображающая множество позиций Р в множестве неотрицательных чисел N. Маркировка изображается с помощью помещаемых внутрь позиций фишек (точек). Так, маркировка сети Петри, приведенной на рис. 1, определяется как m(p1)= m(p3)= 1, m(p2)= m(p4)= m(p5)=0.
Удобно представлять маркировку как n-вектор m=(m1, m2, …,mn) (где n=|P|), каждый элемент которого mi есть m(pi), а также как комплект m, в который входят позиции сети piÎP и #(pi, m) = m(pi). Сеть Петри С с определенной в ней маркировкой m называется маркированной сетью Петри.
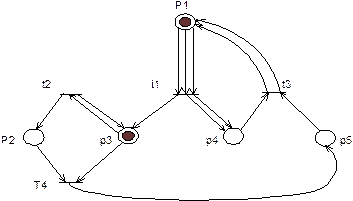 |
Маркировка сети может изменяться в результате запуска переходов. Переход tj маркированной сети Петри С с маркировкой m называется разрешенным, если I(tj)Ím, т.е. в каждой входной позиции tj находиться не меньше фишек, чем из этой позиции исходит дуг в tj. Всякий разрешенный переход может запуститься. В результате запуска перехода tj маркировка сети m изменится на новую: m¢= m- I(tj) + O(tj), т.е. из всякой выходной позиции pi в tj, а в каждую выходную позицию pk помещается столько фишек, сколько дуг ведет из tj в pk. Последовательность запусков переходов называется выполнение сети Петри.
Рассмотрим выполнение сети Петри, изображенной на рис. 1. В начальной маркировке разрешен только переход t2. При его запуске фишка удалится из р3, а затем в позиции р2 и р3 добавится по фишке, т.е. в результате запуска в новой маркировке m¢ появится фишка еще в р2. Теперь становится разрешенным переходы t2, t4. Поскольку запуститься может любой разрешенный переход, предположим, что запускается переход t4. После его запуска из позиции р2 и р3 фишки удаляются, а в позиции р5 появится одна фишка. В получившейся маркировке m² не разрешен ни один переход. На этом выполнение сети Петри заканчивается.
| <== предыдущая | | | следующая ==> |
| Ход работы. Расчет параметров установившихся режимов и потерь электроэнергии в трансформаторах и автотрансформаторах | | | Метран-150 |
Date: 2015-09-02; view: 354; Нарушение авторских прав