Искривление пространства

Среди вереницы странных образов, рожденных новой физикой, наибольший интерес вызывают те, которые относятся к квантовой теории и теории относительности. В своей наиболее разработанной форме, называемой квантовой механикой, квантовая теория по существу занимается изучением всех процессов, происходящих в микромире. На квантовой механике основано наше понимание всех явлений молекулярной, атомной, ядерной и субъядерной физики. Теория относительности изучает свойства пространства, времени и движения. Ее выводы становятся существенными, когда рассматриваемая система движется со скоростью, близкой к скорости света, или в сильном гравитационном поле.

Квантовая физика и теория относительности подрывают здравый смысл во многих аспектах. Не последняя среди их “жертв” – наше интуитивное представление о геометрии. В повседневной жизни метр всегда остается метром. Коль скоро ему дано определение, любую другую единицу длины можно считать заданной раз и навсегда. Мало кому могло бы прийти в голову, что 1 м сегодня мог бы оказаться завтра равным 2 м или что ваш метр равен половине моего метра. Однако теория относительности не только утверждает, что расстояния не абсолютны, т.е. не фиксированы раз и навсегда, но и указывает эксперименты, в которых могли бы выявиться подобные расхождения. Если один наблюдатель движется относительно другого, то при измерении длины одного и того же объекта они получают разные значения. И это несмотря на то что в состоянии покоя оба наблюдателя при измерении длины данного объекта получат в точности один и тот же результат.

Уменьшение расстояния с увеличением скорости называется эффектом сокращения длин Лоренца – Фитцджеральда, в честь сформулировавших его ученых Джорджа Фитцджеральда и Хендрика Антона Лоренца. Это один из основополагающих результатов теории относительности. Сокращение длины становится заметным только при скоростях, близких к скорости света, но существование эффекта не вызывает сомнений. Линейный ускоритель частиц в Стэнфорде (шт. Калифорния, США) представляет собой прямолинейную трубу длиной около 3 км (в нашей системе отсчета). Однако движущиеся в ней электроны обладают скоростями, столь близкими к скорости света, что в их “системе отсчета” длина ускорителя едва достигает 0,3 м! На практике, при проектировании такого ускорителя и работе на нем, следует учитывать эффект сокращения длины.

Если теория относительности лишает смысла понятие расстояния, то квантовая механика еще решительнее подрывает устои”, ставя под сомнение основанное на здравом смысле понятие местоположения. Считается непреложной истиной, что все материальные тела должны где‑то находиться. Каждая субатомная частица, например, входящая в состав нашего тела, непременно должна иметь определенное местоположение. Может ли вообще существовать частица, не находясь где‑то?

Когда физики принялись исследовать понятие местоположения в свете квантовой физики, они с изумлением обнаружили, что оно, вообще говоря, лишено смысла. Источник всех “неприятностей” связан с одним фундаментальным правилом квантовой механики, называемым принципом неопределенности Гейзенберга – в честь немецкого физика Вернера Гейзенберга, который в 20‑х годах нашего столетия явился одним из создателей квантовой механики. Согласно этому принципу, невозможно одновременно точно определить положение и скорость частицы. Можно говорить о скорости (точнее, об импульсе), например, электрона и поставить эксперимент с целью измерения этой величины. Эксперимент даст определенный результат. Аналогичным образом можно при желании определить положение электрона. При этом каждый раз мы будем обнаруживать его в определенном месте. Но чего нам никак не удастся сделать–и что в принципе невозможно, – так это одновременно определить обе характеристики электрона: положение и скорость. Независимо от способа измерения сам акт наблюдения местоположения электрона непредсказуемым образом нарушает его движение. Точно так же измерение импульса электрона “смазывает” данные о его местоположении. Эти два типа измерении просто несовместимы.

Невозможность одновременного определения положения и импульса частицы не следует относить за счет грубого характера эксперимента или недостаточной разрешающей способности прибора, ибо в данном случае мы имеем дело с особенностью, внутренне присущей природе. Само понятие электрона, находящегося в таком‑то месте, становится абсолютно бессмысленным, если мы хотим узнать его импульс.

Все это говорит о том, насколько нелепа попытка представить себе мир атома как пространство, “населенное” вращающимися шариками. Если частица не может одновременно обладать определенными положением и импульсом, то мы не в состоянии разумным образом приписать ей траекторию в пространстве. Нам может быть известно, что в какой‑то момент времени электрон находится в точке А, а в более поздний момент – в точке В, но мы не можем знать, как он попал из А в В. Представление о траектории (или орбите), непрерывно соединяющей исходной и конечный пункты, утрачивается. И в самом деле, мы уже упоминали, что в некоторых технических устройствах электроны проявляют способность “туннелировать” через барьер, исчезая с одной его стороны и внезапно вновь возникая по другую сторону. Это – типично квантовый эффект.

Единственный способ придать смысл столь странному поведению электрона заключается в предположении, что частица попадает из А в В одновременно по всем возможным путям! Это необычное свойство можно легко продемонстрировать, приспособив надлежащим образом эксперимент, впервые поставленный в XIX в. английским физиком Томасом Юнгом. Желая доказать справедливость волновой теории света. Юнг воспользовался явлением интерференции. Интерференция происходит при наложении двух волн. Если гребни одной волны совпадают в гребнями другой волны, то происходит усиление, и волновое движение становится более интенсивным. Если же гребни одной волны приходятся на впадины другой, то волны гасят друг друга, и волновое движение ослабевает.

В эксперименте Юнга (рис. 3) свет от небольшого источника падает на две близко расположенные щели в непрозрачном экране. Изображения щелей проецируются на второй экран. Достигая второго экрана, световые волны от каждой щели интерферируют. Результат интерференции зависит от того, как приходят к экрану волны – “в ногу” или “не в ногу”. Это в свою очередь зависит от того, под каким углом волны падают на экран, и поэтому результат меняется от точки к точке. В итоге мы наблюдаем серию светлых и темных полос, образующихся вследствие того, что световые волны поочередно то усиливают, то гасят друг друга.

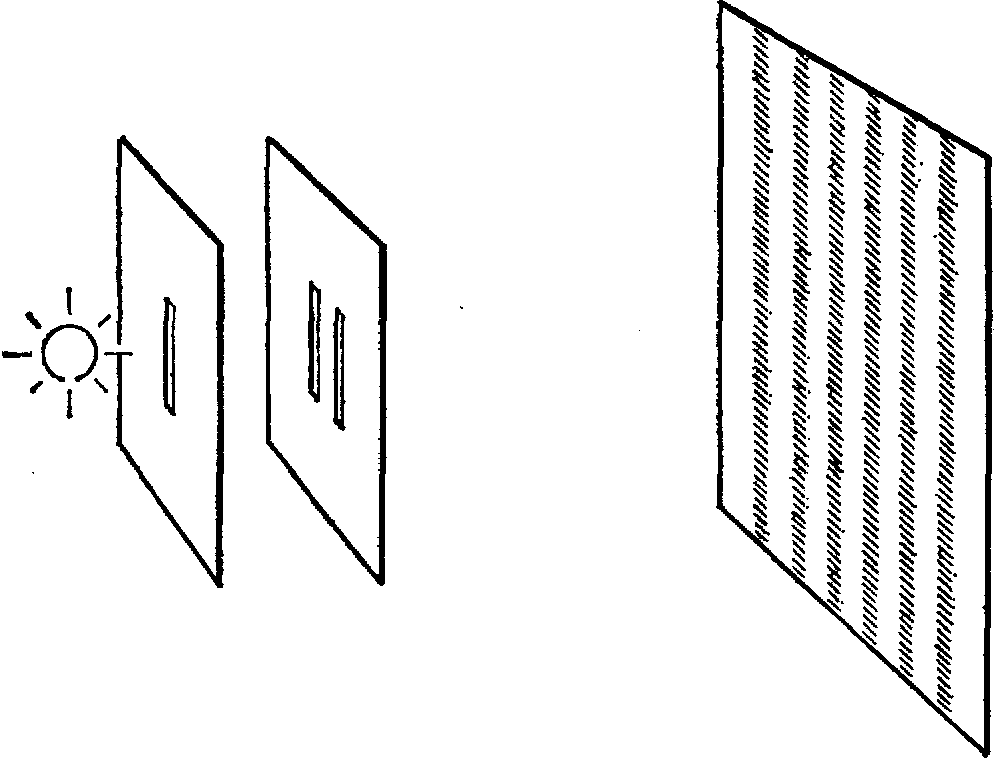
Рис.3. Опыт Юнга по интерференции света. Источник света освещает две параллельные щели в непрозрачном экране. Изображение на экране состоит не из двух светлых полос, а из серии светлых и темных (интерференционных) полос. Этот опыт наглядно демонстрирует волновую породу света, но если взглянуть на него с корпускулярной (фотонной) точки зрения, то многое в опыте покажется странным.

Если принять во внимание квантовую природу света, то обнаруживаются удивительные детали. Квант света – фотон – ведет себя, как частица, в том смысле, что попадает на экран в определенном месте. (Если, желая зафиксировать интерференционную картину, заменить экран фотопластинкой, то каждый фотон вызовет химические изменения в единственном зерне фотоэмульсии в четко определенном месте.) С другой стороны, интерференционная картина явно зависит от наличия двух щелей, порождающих две волны, которые налагаются друг на друга. Если одну щель закрыть, то интерференционная картина исчезает. Наблюдаемое явление нельзя объяснить ссылкой на то, что часть фотонов проходит через одну щель, а часть – через другую, так как интерференционная картина возникает в виде отдельных пятнышек, даже если на экран падают раздельно фотон за фотоном. Единственное возможное объяснение заключается в том, что каждый фотон каким‑то образом проходит через обе щели и достигает экрана, неся на себе отпечаток их существования. Этим “отпечатком” является наибольшая вероятность попадания фотонов в область светлых полос, т.е. в сторону от области темных полос. В этом проявляется сосуществование двух аспектов природы света – волнового и корпускулярного. Хотя первоначально эксперимент был поставлен со светом, аналогичные соображения остаются в силе, если использовать электроны или любые другие квантовые “волны‑частицы”.

Невозможно представить частицу, которая находится “одновременно повсюду”. Можно, по‑видимому, вообразить бесчисленные частицы‑“призраки”, движущиеся по всем возможным путям к точке наблюдения, где они сливаются в “реальную” частицу, но даже подобный образ оказывается неадекватным. Только математика в состоянии свести воедино все эти тонкости.

Вследствие нашей неспособности “прикрепить” частицу к определенному месту в случае нескольких частиц возникают необычные эффекты. Если имеется набор тождественных частиц и мы не можем сказать в каждом отдельном случае, где находится частица, здесь или там, то как можно узнать, где из них какая? Действительно, этого нельзя сделать. Индивидуальность частицы полностью стирается.

Это обстоятельство приводит к важным физическим следствиям. Когда два атома образуют молекулу, на движение электронов вокруг одного из атомов оказывает воздействие другой атом, в результате чего между атомами возникает сила притяжения. Отчасти она обусловлена тем, что данный электрон одного атома не отличим от электронов другого, а из‑за размытости их положения ничто не препятствует этим электронам время от времени меняться местами. Иначе говоря, два электрона из разных атомов могут взаимно заменять друг друга. Подобные обменные взаимодействия (силы), хорошо известные в химии, порождают эффекты, доступные измерениям.

Все это делает понятие расстояния весьма расплывчатым. Но это еще не все. При более тщательном рассмотрении выясняется, что не только размыто положение частицы в пространстве, но и самому пространству присуща размытость. Плохо, когда неизвестно, где находится частица, но если– нельзя сказать, где расположены точки пространства, то все представления геометрии рушатся.

Причина этого дальнейшего осложнения кроется в особых свойствах гравитации. В 1915г. Эйнштейн обобщил теорию относительности, которая предсказывала возможное сжатие и растяжение пространства в зависимости от движения наблюдателя, включив в нее гравитационные явления. Согласно общей теории относительности гравитация представляет собой просто геометрию пустого пространства и времени, однако она совершенно не похожа на ту, которую мы изучаем в школе. Гравитация–это искривленное пространство‑время. Пространство может не только растягиваться и сжиматься, но и изгибаться и скручиваться. Именно такими деформациями пространства объясняется, согласно теории Эйнштейна, гравитация.

Эйнштейн указал ряд примеров, когда искривление пространства и времени можно наблюдать.

Рис.4. Проходя вблизи Солнца, свет от звезды заметно отклоняется из‑за вызванною Солнцем искривления пространства. В результате наблюдаемое нами положение звезды на небе несколько смещено относительно реального.

Один из них – воздействие гравитационного поля Солнца на пространство в его ближайшей окрестности. Во время полного солнечного затмения, когда сияющий диск Солнца заслонен Луной, можно наблюдать небольшие отклонения в положениях звезд, расположенных на небе вблизи Солнца, по сравнению с их координатами, зафиксированными в астрономических атласах (рис. 4). Световые лучи, идущие от звезд, заметно отличаются от прямолинейных, что обусловлено искривлением пространства Солнцем.

Эта и другие проверки теории относительности, основанные на гораздо более сильных гравитационных полях нейтронных звезд, убедили физиков в том, что гравитация действительно искривляет пространство. Одно из следствий этого состоит в том, что пространство (строго говоря, пространство‑время) следует считать как бы упругим, способным изменять свою геометрическую форму. Иначе говоря, мы можем наблюдать динамику пространства. Например, когда звезда коллапсирует, образуя черную дыру, первоначально слабая деформация пространства в ее окрестности стремительно нарастает, создавая чудовищно деформированное пространство – ловушку, из которой ничто не может выйти наружу. Другим примером может служить расширяющаяся Вселенная (см. гл. I): в ней пространство между галактиками непрерывно растягивается.

Способность пространства изменяться и двигаться имеет глубокий смысл для квантовой физики. Принцип неопределенности Гейзенберга размывает не только характер движения частицы, но и динамику пространства. Методом математического моделирования установлено, что в масштабах, по крайней мере в 1020 раз меньших размеров атомного ядра, структура пространства напоминает пену и характеризуется резкими и спонтанными изменениями (увеличением и уменьшением) кривизны. Подобно тому как частица “использует” все доступные ей траектории движения, пространство в ультрамикроскопических масштабах реализует все возможные способы движения. В случае частицы речь шла о мириадах призрачных частиц, движущихся каждая по своей траектории. Аналогично мы можем говорить о бесконечном количестве призрачных пространств, каждое из которых имеет конкретную геометрию.

Такая призрачная динамика пространства предполагает, что в очень малых масштабах само понятие “местоположение” утрачивает смысл. Упорядоченное расположение точек, гладкая непрерывность пространства классической геометрии исчезает в пенообразном пространстве‑времени. Вместо него мы имеем беспорядочное нагромождение полуреальных пространств‑призраков. И в таком беспорядочно изменяющемся океане здравый смысл полностью теряет свою силу.

Спин

Поскольку в квантовом мире положение в пространстве не может быть точно определено, неудивительно, что подобная участь постигает и углы. В повседневной жизни нам кажется само собой разумеющимся, что объекты имеют определенную ориентацию: ваза на столе стоит вертикально, стрелка компаса указывает на север, луч прожектора обшаривает небо. Понятие направления занимает центральное место в выработанной нами мысленной модели мира. Без него представление о внешнем мире утратило бы смысл.

Но в квантовом мире, в масштабе атомов и их составных частей, недопустимо наивное толкование понятий направления и ориентации. Нельзя утверждать, что электрон, обращающийся вокруг атомного ядра, в такой‑то момент времени находится в данном направлении от ядра, так как положение электрона размыто. Пучок фотонов или других частиц нельзя использовать для указания направления, так как частицы не следуют четко определенным траекториям: блуждая, они ведут себя непредсказуемо.

Тем не менее на первый взгляд кажется, что одна многообещающая возможность однозначного определения направления все же существует. Мы уже упоминали, что нейтрино обладают своеобразным собственным вращением, или “спином”. Более того, это свойство присуще почти всем субатомным частицам; особенно отчетливо оно выражено у электронов и кварков. Привлекательно изобразить частицу со спином, например электрон, в виде крохотного шарика, вращающегося вокруг собственной оси, подобно Земле, совершающей суточное вращение. Чтобы такая “картинка” имела смысл, спин должен быть ориентирован в некотором направлении. Если это направление можно установить путем соответствующего измерения, то это означает, что у нас есть способ однозначного определения направления даже на квантовом уровне. Такие измерения действительно можно провести, но при этом возникает совершенно необычная ситуация.

Предположим, что экспериментатор включает прибор и сначала выбирает направление, чтобы измерить относительно него ориентацию спина частицы. На практике в качестве такого направления обычно принимают направление магнитного или электрического поля. Экспериментатор хочет определить угол между спином частицы и направлением поля. Проведя измерение, он с удивлением обнаруживает, что спин ориентирован строго по направлению поля. Эксперимент повторяется многократно, но результат всегда один и тот же: спин всегда ориентирован вдоль выбранного направления. Подозревая неладное, экспериментатор принимается менять направление внешнего поля, но спин частицы неизменно следует за его направлением. И как ни пытается экспериментатор обнаружить спин, направленный под углом к исходному направлению, у него ничего не получается. Экспериментатор в замешательстве: частица как бы читает его мысли, поскольку всегда указывает направление, которое он произвольно выбирает для отсчета.

Отчаявшись, экспериментатор прибегает к дьявольской хитрости задает два различных исходных направления, А и В, и измеряет угол между направлением спина и каждым из них. Поскольку спин частицы, по мнению экспериментатора, не может быть одновременно ориентированным в двух различных направлениях, по крайней мере в одном случае спин образует с одним из них некоторый угол. Исходя из этого, экспериментатор производит первое измерение. То, что спин ориентирован вдоль направления А, не вызывает у него удивления. Второе измерение он проводит сразу же вслед за первым, чтобы спин не успел переориентироваться. Направление В было выбрано так, что составляло угол 250 с направлением А, и экспериментатор, только что с удовлетворением установивший, что спин ориентирован вдоль оси А, естественно, ожидает, что спин будет направлен под углом 250° к оси В. Однако он с изумлением обнаруживает, что природа перехитрила его: частица каким‑то образом упредила его, и ее спин, словно по волшебству, оказался ориентированным вдоль оси В! В ярости экспериментатор принимается вновь измерять угол между направлением спица и осью А и видит, что спин, как и прежде, ориентирован вдоль оси А.

Поразительные эффекты, подобные описанному, стали неотъемлемой частью современной физики, и экспериментаторы давно привыкли к тому, что спин частицы всегда направлен вдоль оси, выбранной за исходную. Это свойство сводит на нет любую попытку придать смысл понятию направления в квантовом мире. Оно также привносит в физический мир элемент странной субъективности. Если спину частицы предопределено следовать за случайно выбранным направлением отсчета, то создается впечатление, что экспериментатор как бы вторгается в микромир. Рабская покорность, с которой все частицы со спином следуют заданному экспериментатором направлению, казалось бы, наводит на мысль, что материальным миром управляет какой‑то высший разум. В гл. 3 мы увидим, что подобные субъективные элементы квантовой физики требуют полного пересмотра традиционных представлений о физической реальности и роли сознания в физическом мире.

Физика частиц со спином таит немало других сюрпризов. Один из них связан с простым, на первый взгляд даже тривиальным, понятием вращения. В повседневной жизни нам всем приходилось сталкиваться о процессом вращения. Представьте себе, что вы стоите в комнате, скажем, лицом к двери. Поворачиваясь вокруг своей вертикальной оси, вы увидите перед собой все новые и новые участки стен и, повернувшись на 180°, окажетесь спиной к двери. Повернувшись еще на 180°, вы окажетесь в исходной позиции–лицом к двери,–совершив полный оборот. Мир будет выглядеть в точности таким, каким был до начала вращения. Казалось бы, что может быть проще и очевиднее?

Но в мире субатомных частиц элементарный акт вращения приводит к удивительному результату. При прохождении электрона через магнитное поле определенной конфигурации его спин может поворачиваться на все больший угол, совершив в конце концов полный оборот на 360°. Основываясь на здравом смысле, естественно ожидать, что электрон вернется в исходное состояние. Однако это не так. Свойства электрона, совершившего поворот спина 360°, заметно отличаются от свойств электрона, не подвергшегося воздействию. Чтобы вернуть в исходное состояние электрон, спин которого совершил поворот, его спин необходимо повернуть дополнительно на 360°, т.е. заставить описать два полных оборота.

Только после этого не обнаружится сколько‑нибудь заметного различия между “повернувшимся” и “неповернувшимся” электронами.

Что это означает? Очевидно, что в простейшем случае необходим поворот на 720°, чтобы совершить полный оборот, т.е. вернуть мир в исходное состояние. Элементарная частица, например электрон, “ощущает” полный оборот в 720°. B мире людей и в случае крупных объектов это свойство утрачено – мы не отличаем один оборот на 360° от следующего. Следовательно, мы в некотором смысле лишь наполовину воспринимаем мир, доступный электрону.

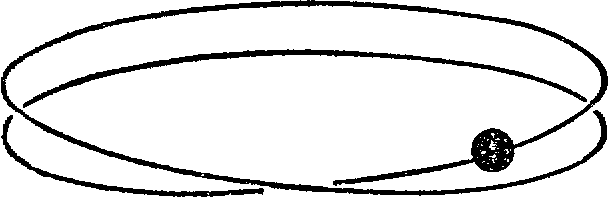
Рис.5. Двойная проволочная петля дает весьма приблизительное представление о свойствах собственного спина. При перемещении на 360° бусина не возвращается в исходное положение – для этого необходим еще один оборот по проволоке, т.е. перемещение еще на 360°. Но на расстоянии столь тонкая особенность не заметна.

Рис. 5 дает простую иллюстрацию сказанного, на нем изображена двойная проволочная петля с нанизанной на нее бусинкой. Издали мы не можем различить два витка, и нам кажется, что проволока просто согнута в окружность. Если бусинка, скользя по проволоке, опишет угол 360°, то мы ожидаем, что она вернется в исходную точку, но приглядевшись внимательнее, обнаруживаем, что это не так. Бусинка должна совершить еще один оборот на 360°, чтобы, обойдя всю петлю, вернуться к началу своего пути.

Это странное “двойственное” представление о мире, присущее электронам и другим микрочастицам, принято считать фундаментальным свойством природы. Оно приводит к многим неожиданным, доступным наблюдению следствиям. Например, создаваемое спином электрона магнитное поле вдвое превышает магнитное поле, которое создавал бы вращающийся заряженный шарик. В дальнейшем мы увидим, что необычная геометрическая природа спина может оказаться ключом к единой теории.

Date: 2015-08-24; view: 393; Нарушение авторских прав