
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задания. Образец экзаменационного задания
|
|
Образец экзаменационного задания
по дисциплине «Математика»
Специальности 210400.62, 210200.62, 201000.62, 150100.62
Курс, группы БРТ-11, БРС-11, ББС-11, БМТ-11
Время экзамена 70 минут
Критерии оценки < 32 % - «неудовлетворительно»
33 % - 60 % - «удовлетворительно»
61 % - 79 % - «хорошо»
80 % - 100 % - «отлично»
Задания
№1. Множество всех первообразных функции имеет вид
Варианты:
А) 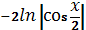 , Б)
, Б) 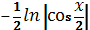 , В)
, В) 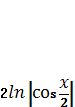 , Г)
, Г) 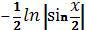 .
.
№2. В неопределенном интеграле 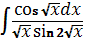 введена новая переменная
введена новая переменная  . Тогда интеграл примет вид:
. Тогда интеграл примет вид:
Варианты:
А) 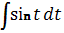 , Б)
, Б)  , В)
, В) 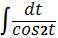 , Г)
, Г) 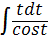 .
.
№3. Если в неопределенном интеграле  , применяя формулу интегрирования по частям:
, применяя формулу интегрирования по частям:  , положить, что
, положить, что 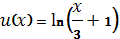 , то функция
, то функция 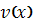 будет равна
будет равна
Варианты:
А)  , Б)
, Б)  , В)
, В) 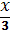 +1, Г)
+1, Г)  .
.
№4. В неопределенном интеграле 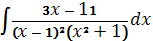 подынтегральная функция разлагается на элементарные дроби
подынтегральная функция разлагается на элементарные дроби
Варианты:
А)  , Б)
, Б) 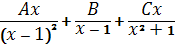 ,
,
В) 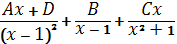 , Г)
, Г)  .
.
№5. Укажите соответствие между неопределенным интегралом и его значением
Варианты:
А) 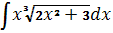 , Б)
, Б)  , В)
, В)  , Г)
, Г)  , Д)
, Д)
1)  , 2), 3), 4)
, 2), 3), 4)  , 5)
, 5) 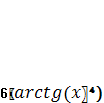
№6. Если при вычислении интеграла 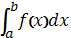 от непрерывной функции сделана подстановка
от непрерывной функции сделана подстановка  , то он равен
, то он равен
Варианты:
А)  , Б)
, Б)  ,
,
В)  , Г)
, Г) 
№7. В определенном интеграле 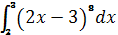 введена новая переменная
введена новая переменная 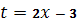 . Тогда интеграл примет вид:
. Тогда интеграл примет вид:
Варианты:
А) 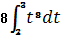 , Б)
, Б)  , В)
, В)  , Г)
, Г) 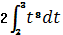 .
.
№8. Площадь криволинейной трапеции, изображенной на рисунке,

равна…
№9. Для функции  справедливы соотношения
справедливы соотношения
Варианты:
А)  , Б)
, Б) 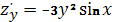 , В)
, В)  ,Г)
,Г) 
№10. Для функции  справедливы соотношения
справедливы соотношения
Варианты:
А)  , Б)
, Б)  , В)
, В)  , Г)
, Г)  ,.
,.
Д) 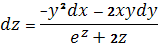 .
.
№11. Для стационарных точек функции  справедливы утверждения
справедливы утверждения
Варианты:
А) их число равно 2, Б) их число равно 3, В) сумма их абсцисс равна 1,
Г) сумма их абсцисс равна 2, Д) сумма их ординат равна 0.
№12. Градиент функции 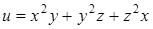 в точке
в точке 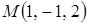 равен…
равен…
Варианты:
А) 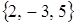 , Б)
, Б)  , В)
, В) 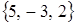 , Г)
, Г)  .
.
№13. Производной функции 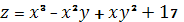 в точке
в точке  в направлении, идущем от этой точки к точке
в направлении, идущем от этой точки к точке 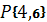 , является
, является
Варианты:
А) вектор {1,17}, Б) вектор {1,-1}, Г) число 5, Д) число 4,2.
№14. Если в двойном интеграле 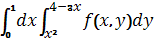 изменить порядок интегрирования, то интеграл примет вид
изменить порядок интегрирования, то интеграл примет вид
Варианты:
А) 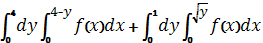 ,
,
Б)  ,
,
В) 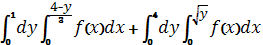 .
.
№15. Интеграл  ,где V:
,где V:  , равен
, равен
№16. Интеграл 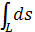 , где
, где 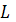 дуга линии
дуга линии  ,
, 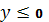 , равен
, равен
№17. Криволинейный интеграл по координатам равен нулю по любому замкнутому контуру
Варианты:
А)  , Б)
, Б)  , В)
, В) 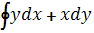 , Г)
, Г) 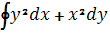 .
.
№18. Используя признак Даламбера, установите соответствие между рядами и следующими утверждениями
Варианты:
А)  , Б)
, Б) 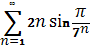 , В)
, В) 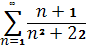
1) расходится 2) сходится
3) с помощью признака Даламбера установить нельзя.
№19. С помощью радикального признака Коши укажите какие из рядов сходятся
Варианты:
А) 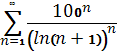 , Б)
, Б) 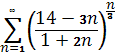 , В)
, В)  , Г)
, Г) 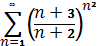 .
.
№20. Область сходимости степенного ряда 
Варианты:
А)  Б)
Б)  В)
В)  Г)
Г) 
№21. Дана функция 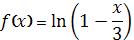 , тогда первые четыре, отличные от нуля, члены разложения этой функции в ряд Маклорена имеют вид
, тогда первые четыре, отличные от нуля, члены разложения этой функции в ряд Маклорена имеют вид
Варианты:
А)  Б)
Б) 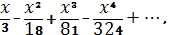
В)  Г)
Г)  .
.
Таблица правильных ответов
| Номер задания | Ответ | Номер задания | Ответ |
| А | А | ||
| Б | Д | ||
| А | Б | ||
| А | |||
| А-1, Б-2, В-3, Г-4 | |||
| Г | В | ||
| В | А-1, Б-2, В-3 | ||
| 3,75 | А,В | ||
| В,Г | Г | ||
| А,В,Д | В | ||
| Б,Г,Д |
Date: 2015-08-24; view: 485; Нарушение авторских прав