
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Повторные независимые испытания
|
|
Практическое занятие № 7 - 8
Формула Бернулли. Если в каждом из п независимых испытаний вероятность появления события А постоянна и равна р, то вероятность того, что в п независимых испытаниях событие А наступит ровно т раз, определяется по формуле Бернулли
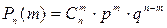 , где
, где 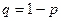 .
.
На практике формулой Бернулли удобно пользоваться, если п не очень велико (п < 10).
Пример 1. Вероятность изготовления на станке детали высшего качества равна 0,8. Найти вероятность того, что из 6 взятых наудачу деталей: а) 4 высшего качества; б) хотя бы одна деталь высшего качества.
Решение. Из условия задачи имеем, что п = 6, т = 4, р = 0,8, q = 1- 0,8 = 0,2. Тогда, применяя формулу Бернулли, получаем
а) 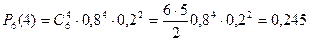 .
.
б) 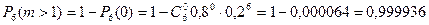 .
.
Наивероятнейшее число появления события А в п независимых испытаниях определяется по формуле
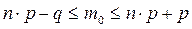 ,
,
где п - число независимых испытаний,
р - вероятность наступления события А в одном испытании,
q - вероятность не наступления события А в одном испытании,
т0 - наивероятнейшее число наступлений событий А.
Пример 2. Монета подбрасывается 3 раза. Найти наиболее вероятное число успехов (выпадений герба).
Решение. Возможными значениями для числа успехов в 3-х рассматриваемых испытаниях являются m = 0, 1, 2 или 3. Пусть Am - событие, состоящее в том, что при 3-х подбрасываниях монеты герб появляется m раз. По формуле Бернулли легко найти вероятности событий Am (см. таблицу):
| m | ||||
| Pn(m) | 1/8 | 3/8 | 3/8 | 1/8 |
Из этой таблицы видно, что наиболее вероятными значениями являются числа 1 и 2 (их вероятности равны 3/8). Этот же результат можно получить и из приведенного выше утверждения.
По условию задачи п=3, р= 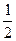 , q=
, q= 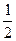 . Тогда, подставляя эти значения в формулу для нахождения наивероятнейшего числа, получаем
. Тогда, подставляя эти значения в формулу для нахождения наивероятнейшего числа, получаем
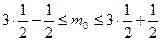 ,
,
 .
.
Приближенная формула Пуассона используется в том случае, когда число испытаний n – велико, а вероятность успеха в отдельном испытании мала (p<0,1). Тогда вероятность того, что в п испытаниях событие А наступит т раз, определяется приближенно формулой
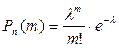 , где
, где 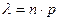 .
.
Пример 3. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что изделие в пути повредится р = 0,0002. Найти вероятность того, что в пути повредится только 3 изделия.
Решение. Применяем формулу 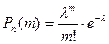 , где
, где 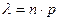
По данным задачи 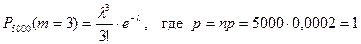 .
.
Тогда 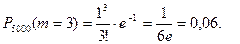
Закон Пуассона еще называют законом редких явлений.
Пример 4. Известно, что процент брака для некоторой детали равен 0,5%. Контролер проверяет 1000 деталей. Какова вероятность обнаружить ровно 3 бракованных детали? Какова вероятность обнаружить не меньше 3-х бракованных деталей?
Решение. Имеем 1000 испытаний Бернулли с вероятностью «успеха» р=0,005. Применяя пуассоновское приближение с 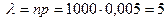 , получаем
, получаем
P1000(3)» 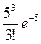 ,
,
P1000(m³3)=1-P1000(m<3)=1-[ 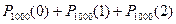 ]»1-
]»1- 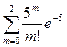 и по таблицам находим Р1000(3)»0,14, Р1000(m³3)»0,875.
и по таблицам находим Р1000(3)»0,14, Р1000(m³3)»0,875.
Дополнение о значении закона Пуассона.
Формула Пуассона используется также для расчета вероятности появления различного числа событий (точек) в какой-либо области (площади, объеме или во времени).
Если указано среднее число 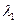 появления точек на единицу области (площади, объема, времени), то число
появления точек на единицу области (площади, объема, времени), то число 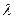 точек, попадающих в область s, внутри которой появляются интересующие нас события (точки), определяется произведением среднего числа
точек, попадающих в область s, внутри которой появляются интересующие нас события (точки), определяется произведением среднего числа 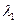 и размера области s, т.е.
и размера области s, т.е. 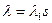 . В этом случае вероятность
. В этом случае вероятность 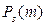 появления m событий (точек) в области s определяется формулой Пуассона
появления m событий (точек) в области s определяется формулой Пуассона
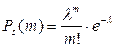 , где
, где 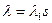 .
.
Пример 5. При определении зараженности зерна установлено, что в 1 кг содержится в среднем 10 вредителей. Определите вероятность того, что в 100 г не встретится ни одного вредителя.
Решение. По условию задачи среднее число точек (вредителей, содержащихся в 1кг зерна) равно 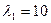 , размер области
, размер области  . Следовательно,
. Следовательно, 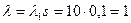 и искомая вероятность равна
и искомая вероятность равна
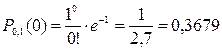
Локальная теорема Муавра-Лапласа. Если производится п независимых испытаний (п - велико), и вероятность наступления события А в каждом испытании постоянна и равна р, то вероятность того, что в п независимых испытаниях событие А наступит m раз, определяется по формуле
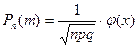 ,
,
где 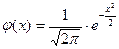 ,
, 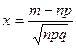 ,
,
причем результат тем точнее, чем ближе значение р к 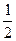 и чем больше п.
и чем больше п.
Функция 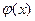 - четная, т.е.
- четная, т.е. 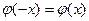 и для положительных значений х составлена таблица ее значений.
и для положительных значений х составлена таблица ее значений.
Замечание. В таблице приведены значения функции 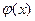 при
при 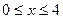 , при
, при 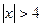 | полагают
| полагают 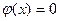 .
.
Пример 6. На опытном поле посеяно 900 семян. Найдите вероятность того, что всходы дадут ровно 800 семян, если вероятность всхода каждого зерна равна 0,9.
Решение. По условию задачи имеем: р = 0,9, q = 1-0,9 = 0,1, п= 900, m =800. Тогда, применяя локальную теорему Лапласа, находим
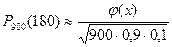 ,
, 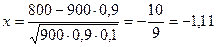
Из таблицы находим значение функции 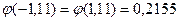 . Тогда
. Тогда 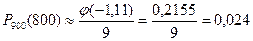
Интегральная теорема Муавра-Лапласа. Если вероятность р наступления события А в каждом из п независимых испытаний постоянна и отлична от нуля и единицы, то вероятность того, что в п независимых испытаниях событие А наступит не менее чем 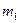 раз и не более чем
раз и не более чем 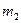 раза, определяется по формуле
раза, определяется по формуле
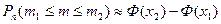 ,
,
где, 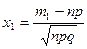 ,
, 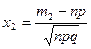 , а
, а 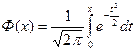 – функция Лапласа.
– функция Лапласа.
Функция Ф(х) – нечетная, т.е. Ф(-х) = -Ф(х). Для функции Ф (х) составлены специальные таблицы при положительных значениях аргумента, причем при х > 5 полагают Ф(х) = 0,5.
Пример 7. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение. По условию задачи: п= 400, т1= 70, т2= 100, р= 0,2, q =0,8. Применяя интегральную теорему Лапласа, получаем 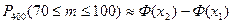
где 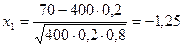 и
и 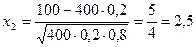
Находим значения функции Ф(х) по таблице
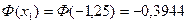 ,
, 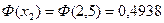
Тогда искомая вероятность равна
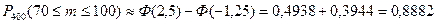
Используя интегральную формулу Муавра-Лапласа можно вычислить вероятность того, что частота появления события А в n независимых испытаниях (т.е. число m/n) отклонится от вероятности p события А не более чем на положительную величину e: 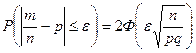 .
.
Пример 8. Вероятность того, что деталь нестандартна, равна 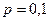 . Найдите, сколько деталей надо отобрать, чтобы с вероятностью 0,9544 можно было утверждать, что относительная частота появления нестандартных деталей (среди отобранных) отклонится от постоянной вероятности р по абсолютной величине не более, чем на 0,03.
. Найдите, сколько деталей надо отобрать, чтобы с вероятностью 0,9544 можно было утверждать, что относительная частота появления нестандартных деталей (среди отобранных) отклонится от постоянной вероятности р по абсолютной величине не более, чем на 0,03.
Решение. По условию 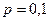 ,
, 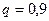 ,
, 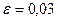 ,
, 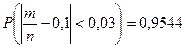 . Требуется найти n.
. Требуется найти n.
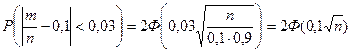 .
.
Получаем 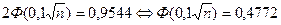
По таблице для функции Лапласа определяем 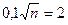 , отсюда
, отсюда 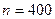 .
.
Date: 2015-07-27; view: 2512; Нарушение авторских прав