
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример кинематического анализа рычажного механизма
|
|
Кривошип О1А вращается с постоянной угловой скоростью 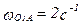 . Определить для заданного положения механизма:
. Определить для заданного положения механизма:
1. Скорости точек А, В, D … механизма и угловые скорости всех его звеньев с помощью плана скоростей.
2. Скорости этих же точек и угловые скорости звеньев с помощью мгновенных центров скоростей.
3. Ускорения точек А и В, средней точки звена АВ и угловое ускорение звена при помощи плана ускорений звена АВ.
4. Ускорения этих же точек при помощи аналитического метода определения ускорений.
Построение плана механизма
На основании данных, представленных в табл.1, строим план механизма.
Таблица 1. Исходные данные
| φ, град | Расстояние, см | Длина звена, см | Угол, град | ||||||||||
| а | b | c | d | O1A | АВ | AD | DE | EO2 | CO2 | CG | α | β | |
1. Выбираем масштаб длин. Пусть длина кривошипа (звена О1А) будет равна на плане 22 мм. Тогда масштабный коэффициент 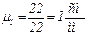 .
.
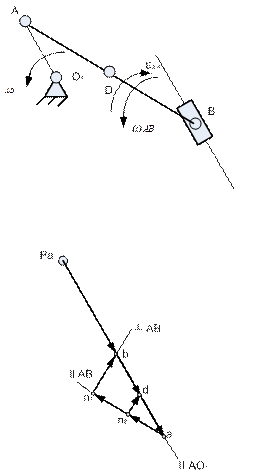
2. Изображаем кривошип под углом 60° к горизонтали. Отмечаем точку А (рис. 21).
3. Проводим дугу окружности с центром в точке А радиусом АВ.
4. Определяем положение горизонтальной направляющей ползуна G, находящейся на расстоянии b от шарнирной опоры О 1.
5. Определяем положение шарнирной опоры О2, находящейся на расстоянии с от горизонтальной направляющей ползуна G и расстоянии а от опоры О1
6. Определяем положение наклонной направляющей ползуна В. Для этого проводим дугу окружности радиусом d и строим прямую, составляющую 30° с вертикалью и проходящую через точку О2 таким образом, чтобы она являлась касательной к этой окружности.
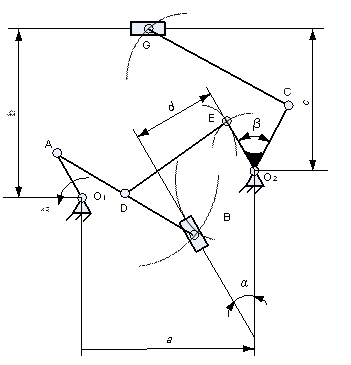
Рис. 21. План плоского многозвенного рычажного механизма
7. Находим положение ползуна на наклонной направляющей в данный момент времени (точка В). Это есть точка пересечения окружности радиуса АВ и направляющей.
8. Точка D делит звено АВ пополам.
9. Определяем положение точки Е. Для этого проводим дугу окружности радиусом DE. Затем из точки О2 проводим дугу окружности радиусом О2Е. Точка пересечения двух окружностей и даст положение точки Е в данный момент времени.
10. Откладываем от отрезка О2Е угол 60° в направлении движения по часовой стрелке. Затем на полученной прямой – отрезок О2С.
11. Положение точки G в данный момент времени определится пересечением окружности радиуса СG и горизонтальной направляющей ползуна G.
Построение плана скоростей
Отметим, что определяемые кинематические величины носят мгновенный характер, т.е. меняются с течением времени в одних случаях по направлению, в других – по величине, в третьих – и по величине и по направлению.
1. Определяем скорость точки А кривошипа О1А. Поскольку кривошип движется вращательно, то модуль 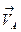 определяется так:
определяется так:
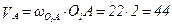 (см/c),
(см/c), 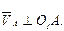
Выбираем полюс плана скоростей РV. Вектор скорости точки А направлен в сторону вращения кривошипа (рис. 22).
Исходя из удобства построения чертежа и его размеров, выбираем масштаб плана скоростей. Пусть длина вектора скорости точки А  будет равна 44 мм. Тогда масштабный коэффициент
будет равна 44 мм. Тогда масштабный коэффициент 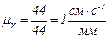 . Из полюса плана скоростей под углом 90° к направлению кривошипа проводим вектор
. Из полюса плана скоростей под углом 90° к направлению кривошипа проводим вектор 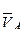 .
.
2. Определяем скорость точки В – 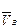 . Для этого необходимо записать систему векторных уравнений для скорости точки В, используя свойства плоскопараллельного движения тела и сложного движения точки:
. Для этого необходимо записать систему векторных уравнений для скорости точки В, используя свойства плоскопараллельного движения тела и сложного движения точки:
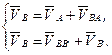
Здесь 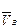
 – абсолютная скорость точки В;
– абсолютная скорость точки В; 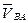 – скорость точки В в относительном вращении вокруг полюса А;
– скорость точки В в относительном вращении вокруг полюса А;  – скорость точки В относительно В/. Точка В/ находится на направляющей ползуна (под ползуном), а точка В – непосредственно на ползуне. Поскольку В/ принадлежит неподвижной направляющей, то ее скорость равна 0. Тогда система уравнений приобретает следующий вид:
– скорость точки В относительно В/. Точка В/ находится на направляющей ползуна (под ползуном), а точка В – непосредственно на ползуне. Поскольку В/ принадлежит неподвижной направляющей, то ее скорость равна 0. Тогда система уравнений приобретает следующий вид:
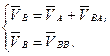
Далее из конца вектора 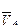 проводим прямую, перпендикулярную звену АВ, на которой будет лежать вектор скорости относительного вращения звена АВ вокруг полюса А –
проводим прямую, перпендикулярную звену АВ, на которой будет лежать вектор скорости относительного вращения звена АВ вокруг полюса А – 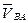 . И из полюса плана скоростей проводим прямую, параллельную направляющей ползуна В, на которой будет лежать вектор скорости точки В –
. И из полюса плана скоростей проводим прямую, параллельную направляющей ползуна В, на которой будет лежать вектор скорости точки В – 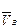 . Абсолютная скорость ползуна равна в данном случае его относительной скорости по отношению к направляющей, что отражено в уравнении. Точка пересечения построенных прямых – точка В. Направление векторов определяем в соответствии с правилами векторного суммирования согласно системе уравнений. Из плана скоростей определяем длины векторов
. Абсолютная скорость ползуна равна в данном случае его относительной скорости по отношению к направляющей, что отражено в уравнении. Точка пересечения построенных прямых – точка В. Направление векторов определяем в соответствии с правилами векторного суммирования согласно системе уравнений. Из плана скоростей определяем длины векторов 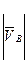 = Pvb =23,5 мм и
= Pvb =23,5 мм и 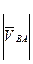 = ab=50мм.
= ab=50мм.
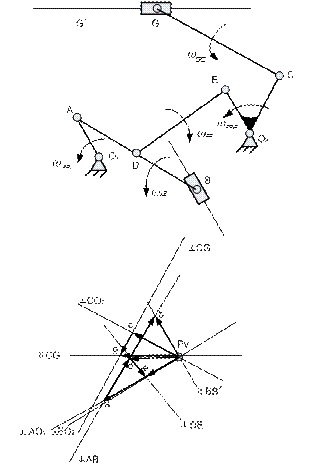
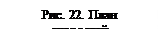
Умножая эти значения на масштабный коэффициент плана скоростей, определяем величины абсолютной и относительной скоростей точки В
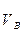 =23,5 см/с и
=23,5 см/с и 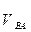 =50 см/с.
=50 см/с.
3.Определяем скорость точки D. Она принадлежит звену АВ, поэтому её скорость определяется из пропорционального отношения отрезков на плане скоростей и отрезков на плане механизма:
ad/АD = ab/AB.
Отсюда ad = 25 мм. Длина полученного отрезка – это длина вектора относительной скорости 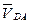 . Конец вектора
. Конец вектора 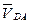 находится в точке d. Соединяя полученную точку с полюсом Pv, получаем вектор абсолютной скорости точки D. Находим длину вектора
находится в точке d. Соединяя полученную точку с полюсом Pv, получаем вектор абсолютной скорости точки D. Находим длину вектора 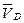 :
: 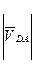 = PVd = 25 мм. Умножая длины полученных отрезков на масштабный коэффициент плана скоростей, находим величины абсолютной и относительной скоростей точки D:
= PVd = 25 мм. Умножая длины полученных отрезков на масштабный коэффициент плана скоростей, находим величины абсолютной и относительной скоростей точки D:
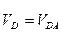 = 25 см/c.
= 25 см/c.
4. Запишем систему векторных уравнений для скорости точки Е:
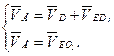
Во втором уравнении системы абсолютная скорость точки Е равна относительной вращательной скорости точки Е вокруг полюса О2. Но точка О2 неподвижна (жёсткое звено ЕО2С совершает вращательное движение относительно оси, проходящей через точку О2), поэтому абсолютная скорость равна относительной.
По аналогии со скоростью точки В из конца вектора 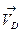 проводим перпендикуляр к направлению звена ED. Затем из полюса плана скоростей PV строим прямую, перпендикулярную отрезку ЕО2, и находим точку пересечения полученных прямых. Это будет точка е. Расставляем векторы в соответствии с правилами векторного суммирования. Из плана определяем длины векторов:
проводим перпендикуляр к направлению звена ED. Затем из полюса плана скоростей PV строим прямую, перпендикулярную отрезку ЕО2, и находим точку пересечения полученных прямых. Это будет точка е. Расставляем векторы в соответствии с правилами векторного суммирования. Из плана определяем длины векторов:
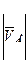 = PVe =20 мм и
= PVe =20 мм и 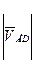 = ed=12,5мм.
= ed=12,5мм.
Умножая эти значения на масштабный коэффициент плана скоростей, определяем величины скоростей:
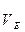 =20 см/с и
=20 см/с и 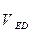 =12,5 см/с.
=12,5 см/с.
5. Поскольку звено ЕО2С жёсткое, то точки Е и С движутся относительно опоры О2 во вращении отрезков ЕО2 и СО2 с одинаковой угловой скоростью 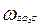 , поэтому модуль скорости точки С найдём из пропорции
, поэтому модуль скорости точки С найдём из пропорции
 .
.
Отсюда 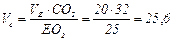 см/c.
см/c.
Направление вектора скорости точки С найдём, отложив на плане скоростей прямую под углом 60° к направлению вектора 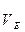 по ходу часовой стрелки (так, чтобы на плане образовалась фигура, подобная жёсткому звену ЕО2С) и разделив значение скорости точки С на масштабный коэффициент плана скоростей. Получив длину отрезка PVс, отложим этот отрезок на данной прямой.
по ходу часовой стрелки (так, чтобы на плане образовалась фигура, подобная жёсткому звену ЕО2С) и разделив значение скорости точки С на масштабный коэффициент плана скоростей. Получив длину отрезка PVс, отложим этот отрезок на данной прямой.
6. Скорость точки G определяем из системы векторных уравнений:
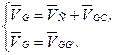
Из точки с на плане скоростей проводим перпендикуляр к направлению звена CG, а из полюса – горизонталь (параллель GG/). Точка пересечения этих двух прямых даст точку G. Отмечаем вектора и находим их длины:
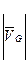 = PVg =29 мм и
= PVg =29 мм и 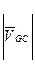 =gc =13 мм.
=gc =13 мм.
Умножая на масштабный коэффициент полученные отрезки, получаем относительную и абсолютную скорости точки G:
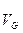 =29 см/с и
=29 см/с и 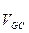 =13 см/с.
=13 см/с.
Определение мгновенных угловых скоростей звеньев механизма с помощью плана скоростей
Модули угловых скоростей звеньев будем определять как отношения скоростей относительного вращательного движения к длинам соответствующих звеньев.
1. Угловая скорость звена АВ:
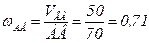 с-1 .
с-1 .
2. Угловая скорость звена ED:
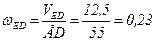 с-1.
с-1.
3. Угловая скорость звена ЕО2С:
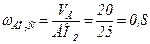 с-1.
с-1.
4. Угловая скорость звена СG:
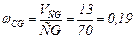 с-1.
с-1.
Направления вращения звеньев в данный момент времени указываем, исходя из направления векторов относительных скоростей на плане скоростей.
Построение плана ускорений для звена АВ механизма
и определение его углового ускорения при помощи плана ускорений
Построение плана ускорений, так же как и плана скоростей, начинаем с определения ускорения той точки, которая принадлежит входному звену механизма. Это точка А. Данная точка участвует во вращательном движении кривошипа О1А относительно опоры О1, причём вращение кривошипа равномерное. Поэтому абсолютное ускорение точки А будет равно одной только нормальной составляющей ускорения и его модуль определится как
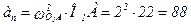 см/c2.
см/c2.
Ускорение точки А направлено по радиусу описываемой точкой А окружности в процессе движения к её центру (рис. 23).
Выбираем масштабный коэффициент плана ускорений 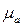 :
: 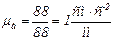 .
.
Выбираем положение полюса плана ускорений Ра . Из полюса параллельно направлению кривошипа О1А от точки А к точке О1 проводим вектор Ра а длиной 44 мм. Отмечаем точку а.
Найдём ускорение точки В. Для этого составляем систему векторных уравнений для ускорения точки В:
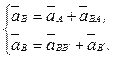
Запишем систему уравнений, выразив полные относительные ускорения через их нормальные и касательные составляющие:
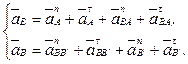
Здесь 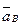 – абсолютное ускорение точки В;
– абсолютное ускорение точки В; 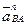 и
и 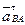 – нормальная и касательная составляющие ускорения точки В в относительном вращательном движении вокруг полюса А;
– нормальная и касательная составляющие ускорения точки В в относительном вращательном движении вокруг полюса А; 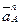 и
и 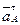 – нормальная и касательная составляющие ускорения точки А.
– нормальная и касательная составляющие ускорения точки А.
Поскольку звено О1А вращается с постоянной угловой скоростью (о чём уже упоминалось), касательная составляющая ускорения 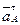 будет равна 0. Ускорения
будет равна 0. Ускорения 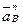 и
и 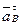 равны 0, поскольку В / принадлежит неподвижной направляющей ВВ/. Нормальная составляющая ускорения точки В ползуна относительно В /
равны 0, поскольку В / принадлежит неподвижной направляющей ВВ/. Нормальная составляющая ускорения точки В ползуна относительно В / 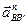 также равна 0, поскольку ползун совершает возвратно-поступательное движение. С учетом этих факторов система уравнений приобретает следующий вид:
также равна 0, поскольку ползун совершает возвратно-поступательное движение. С учетом этих факторов система уравнений приобретает следующий вид:


Величина нормального ускорения в относительном вращательном движении звена АВ вокруг точки А 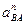 будет равна
будет равна
 см/с2.
см/с2.
Длина вектора 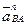 на плане ускорений определится как отношение величины этого нормального ускорения к масштабному коэффициенту плана ускорений:
на плане ускорений определится как отношение величины этого нормального ускорения к масштабному коэффициенту плана ускорений:
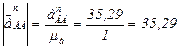 мм.
мм.
Из точки а проводим прямую, параллельную направлению звена АВ и на ней откладываем вектор 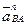 таким образом, чтобы он был направлен от точки В к точке А (центру относительного вращения). Получаем точку n1. Касательное ускорение в относительном вращательном движении звена АВ
таким образом, чтобы он был направлен от точки В к точке А (центру относительного вращения). Получаем точку n1. Касательное ускорение в относительном вращательном движении звена АВ 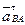 неизвестно ни по величине, ни по направлению, но лежит на перпендикуляре к нормальному ускорению
неизвестно ни по величине, ни по направлению, но лежит на перпендикуляре к нормальному ускорению 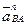 (направлению шатуна АВ). Поэтому из точки n1 проводим перпендикуляр к звену АВ. Из полюса плана ускорений проводим параллель направляющей ползуна В, поскольку абсолютное ускорение точки В равно касательной составляющей относительного возвратно-поступательного движения ползуна вдоль направляющей. Точка пересечения двух перпендикуляров и даст искомую точку b плана ускорений.
(направлению шатуна АВ). Поэтому из точки n1 проводим перпендикуляр к звену АВ. Из полюса плана ускорений проводим параллель направляющей ползуна В, поскольку абсолютное ускорение точки В равно касательной составляющей относительного возвратно-поступательного движения ползуна вдоль направляющей. Точка пересечения двух перпендикуляров и даст искомую точку b плана ускорений.
В данном примере направления кривошипа и направляющей ползуна В совпадают, поэтому вектор ускорения точки А и вектор полного ускорения ползуна лежат на одной прямой. Расставляем векторы в соответствии с правилами векторного суммирования и согласно векторным уравнениям для ускорения точки В.
Определяем длины отрезков Раb и n1 b, соответствующие полному ускорению точки В и его касательной составляющей в относительном вращении:
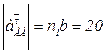 мм;
мм; 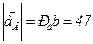 мм.
мм.
Значения соответствующих модулей ускорений:
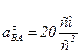 ;
; 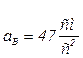 .
.
Модуль полного ускорение точки В в относительном вращательном движении вокруг полюса А:

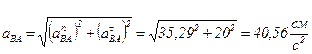 .
.
Находим ускорение точки, делящей звено АВ пополам. В данном случае, это точка D. Точка d будет лежать на плане ускорений между точками а и b и делить отрезок аb пополам (аналогично скоростям). Касательная, нормальная составляющая и полное ускорение точки D в относительном вращении вокруг полюса А будут составлять половину соответствующих ускорений точки В:
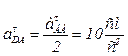 ;
; 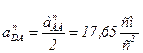 ;
; 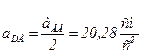 .
.
Модуль полного ускорения точки D определится как произведение длины отрезка Раd на масштабный коэффициент плана ускорений μа:
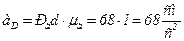 .
.
В данном примере длина векторы ускорения точки D 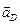 равна скалярной разности длин векторов ускорения точки А
равна скалярной разности длин векторов ускорения точки А 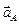 и относительного ускорения
и относительного ускорения 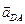 , поскольку все эти векторы лежат на одной прямой.
, поскольку все эти векторы лежат на одной прямой.
Определим модуль мгновенного углового ускорения звена АВ 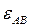 как отношение касательного ускорения
как отношение касательного ускорения 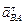 в относительном вращательном движении к длине звена АВ:
в относительном вращательном движении к длине звена АВ:
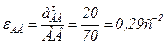 .
.
Направление углового ускорения 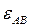 определится вектором относительного касательного ускорения
определится вектором относительного касательного ускорения 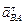 . Из плана ускорений видно, что вращение шатуна АВ в данный момент времени – замедленное.
. Из плана ускорений видно, что вращение шатуна АВ в данный момент времени – замедленное.
| <== предыдущая | | | следующая ==> |
| Письменное умножение и деление многозначных чисел (М-4, ч.1, с.72) | | | Требования к оформлению отчета. Кафедра вычислительной техники и инженерной кибернетики |
Date: 2015-08-15; view: 709; Нарушение авторских прав