
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Колебательное звено
|
|
Звено описывается дифференциальным уравнением второго порядка
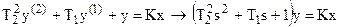
При этом корни характеристического уравнения
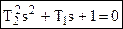
должны быть комплексными
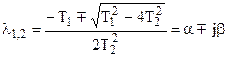 , т.к.
, т.к. 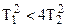 ,
,
где  ,
,  .
.
1) Левая часть уравнения может быть представлена в следующем виде
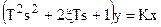 →
→ 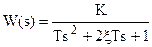 ,
,
где Т = Т2, 2ξТ = Т1 → 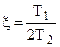 < 1, т.к.
< 1, т.к. 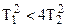 , Т1 < 2Т2.
, Т1 < 2Т2.
Тогда 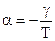 ,
, 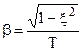
ξ – коэффициент затухания (0 ≤ ξ ≤1).
2) Второй вариант уравнения колебательного звена.
Поделим уравнение на Т2:
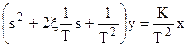 .
.
Обозначим 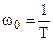 , тогда
, тогда 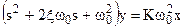 и ПФ будет равна
и ПФ будет равна
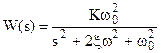 - в радиотехнике и электротехнике,
- в радиотехнике и электротехнике,
где 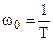 - собственная частота колебаний.
- собственная частота колебаний.
Примеры:
1)
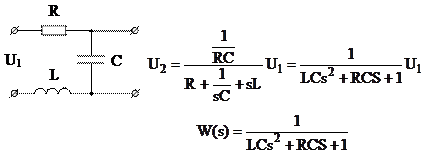 |
Условие колебательности: 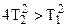 или
или 
4(LC) > (RC2) → 4L > R2C → 
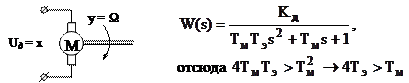 2)
2)
3) Колебательным звеном иногда приближенно представляется замкнутый контур регулирования. Он обычно имеет частотную характеристику следующего вида
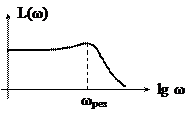 |
Замечание. Колебательное звено может быть выражено через коэффициенты α и β сопряженных корней.
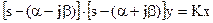
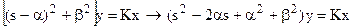
или

Отсюда
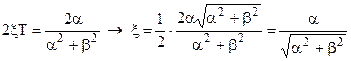 .
.
Временные характеристики:
Переходная характеристика имеет следующий вид:
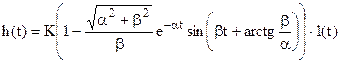
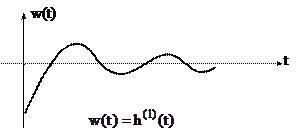 | |||
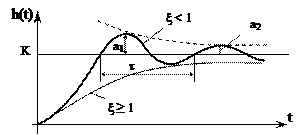 | |||
По экспериментальной характеристике h(t) можно найти параметры колебательного звена:
1) K = hуст.(∞), при x = 1(t), 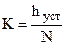 при
при 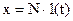 .
.
2) 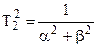 ,
, 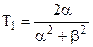 – из уравнения.
– из уравнения.
Согласно решения h(t) величина β является частотой колебаний. Из графика имеем:
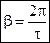 , где τ – период колебаний.
, где τ – период колебаний.
α – характеризует степень затухания.
Его тоже можно найти из графика h(t):
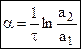 , при а1 = а2 →
, при а1 = а2 →  , т.е. периодические колебания.
, т.е. периодические колебания.
Частотные характеристики:
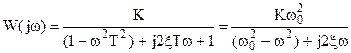
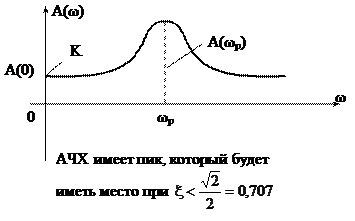

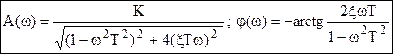
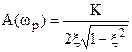 - высота пика зависит от ξ;
- высота пика зависит от ξ;
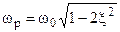 - резонансная частота тоже зависит от ξ и от ω0.
- резонансная частота тоже зависит от ξ и от ω0.
Доказательство: Знаменатель А(ω) 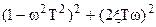 имеет максимум. Поэтому возьмем от него первую производную по ω и приравняем нулю:
имеет максимум. Поэтому возьмем от него первую производную по ω и приравняем нулю:
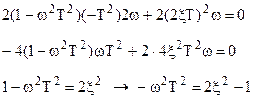
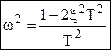 ; →
; → 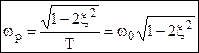
Отсюда видно, что резонанс возникает при 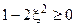 или при
или при 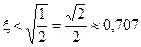 .
.
Теперь
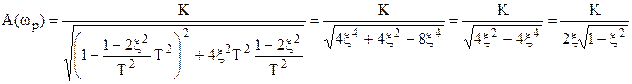 ;
;
очевидно при 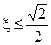 .
.
Т.е. этой формуле всегда нужно брать 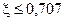 .
.
ЛАЧХ, ФЧХ колебательного звена были построены ранее в виде асимптотической ЛАЧХ.
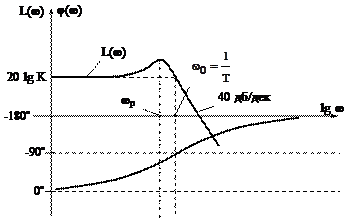 |
Замечание: Здесь ωр не совпадает с ω0; т.к. 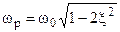 , т.е. ωр < ω0. совпадение произойдет при ξ = 0, но это идеализация, т.к. резонанс = ∞.
, т.е. ωр < ω0. совпадение произойдет при ξ = 0, но это идеализация, т.к. резонанс = ∞.
Асимптотическая ЛАЧХ имеет допустимую погрешность при 0,4 < ξ < 0,7:
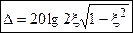 - это выброс на резонансной частоте, а ранее ∆ определялись при
- это выброс на резонансной частоте, а ранее ∆ определялись при 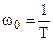 .
.
Отсюда видно, что min достигается при вполне определенном значении ξ.
Пример:
Определим это значение из условия ∆ = 0, отсюда
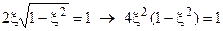
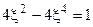 →
→ 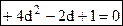
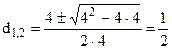 →
→ 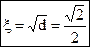 .
.
Вывод: Асимптотическая ЛАЧХ наилучшее приближение имеет при 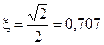 .
.
Примечание: Если ξ ≥ 1, то колебательное звено трансформируется в апериодическое звено 2-го порядка.
 |
|
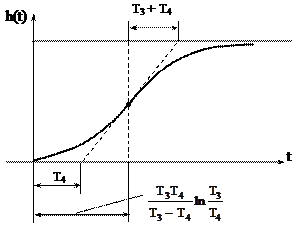
|
 Еще одним частным случаем является ξ = 0 или Т1 = 0. в результате резонанс = ∞. Такое звено называется консервативным. На практике ТАУ их нет.
Еще одним частным случаем является ξ = 0 или Т1 = 0. в результате резонанс = ∞. Такое звено называется консервативным. На практике ТАУ их нет.
ωр = ω0, φ (ω) = - π → (-180˚)
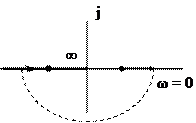 Переходная характеристика h(t) – незатухающие гармонические колебания (синус.)
Переходная характеристика h(t) – незатухающие гармонические колебания (синус.)
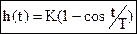
Date: 2015-08-15; view: 985; Нарушение авторских прав
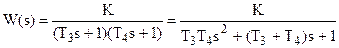 ,
,
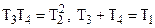 →
→ 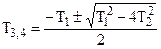 .
Но это уже не типовое звено.
.
Но это уже не типовое звено.
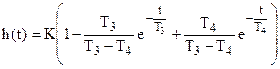 ,
T3 > T4
Т.е. из графика h(t) можно определить T4 и T3. (даже с проверкой, т.к. 3 соотношения)
,
T3 > T4
Т.е. из графика h(t) можно определить T4 и T3. (даже с проверкой, т.к. 3 соотношения)