
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

На практике используют десятичный логарифм из-за удобства расчетов (кратность числу десять)
|
|
Лекция 5: Логарифмические частотные характеристики
Получение логарифмических частотных характеристик.
Прологарифмируем ЧПФ W(jω) = A(ω)ejφ(ω):
ln W(jω) = ln A(ω) + jφ(ω).
Вывод: Логарифмическая форма состоит не из произведения АЧХ и ФЧХ, а из суммы этих составляющих. Это удобно, т.к. позволяет строить и исследовать их раздельно.
На практике используют десятичный логарифм из-за удобства расчетов (кратность числу "десять").
История:
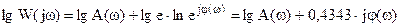 , т.е. тот же результат.
, т.е. тот же результат.
В начале 20 века фирма Белл (телеграфия) вела работы по передаче сигналов по линиям и исследовала их затухание. Сигнал оценивался мощностью, которая, как известно, пропорциональна квадрату амплитуды (напряжения  или тока I2R).
или тока I2R).
В результате для логарифмической амплитудно-частотной характеристики (ЛАЧХ) было получено соотношение
 ,
,
где А(ω) – отношение амплитуд.
Эту ЛАЧХ L(ω) стали измерять в беллах. Т.к. 1 белл равен десятикратному изменению мощности  , то десятикратное изменение амплитуды = 2 беллам. Т.к.
, то десятикратное изменение амплитуды = 2 беллам. Т.к. 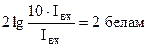 , стократное изменение амплитуды:
, стократное изменение амплитуды:  .
.
Это слишком большая величина для оценки небольших изменений, поэтому для удобства в ТАУ шкалу растянули, введя новую единицу измерения децибел за счет ввода в выражение L(ω) дополнительного коэффициента = 10. В результате получилась формула, которая используется и в связи, теоретическом управлении и телефонии и т.п. следующего вида: L(ω) = 20 lg A(ω) [дБ].

| L = 20 lgA, дБ |
| ||
| 10 000 | ||||
| 10 000 000 | ||||
| 10 млн. | порог для разрушения уха |
Замечание: Величина модуля A(ω) должна быть безразмерной величиной. Это часто выполняется, например, электронные регуляторы, передаточная функция разомкнутой САУ и т.п. Однако, и для размерных величин и A(ω) осуществляется логарифмирование, а исходная размерность приписывается результату, например lgω принимают за  .
.
Логарифмическая шкала и ее координаты
Для построения ЛАЧХ и ЛФЧХ требуется стандартная логарифмическая сетка. По оси абсцисс откладывается lgω, а по оси ординат L(ω). Ось ординат не проходит через ω = 0, т.к. lg 0 = -∞. Оси ординат φ(ω) и L(ω) можно проводить раздельно, но их совмещают.
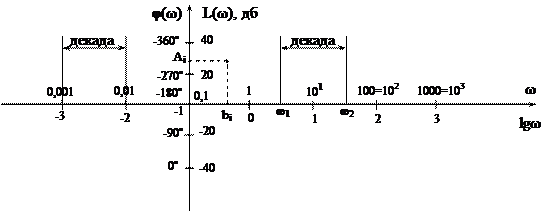 |
Местоположение оси L(ω) определяется частотным диапазоном (полосой пропускания) динамического звена (сист.), чтобы последний хорошо просматривался на рисунке.
Для построения φ(ω) используется эта же шкала при этом ось абсцисс совмещают с φ = -180˚, что удобно при оценке качества системы, ее устойчивости и при синтезе. С практической точки зрения положительная фаза (нарастание, сдвиг) откладывается вниз (как на рисунке) – это не догма, фаза φ(ω) откладывается в равномерном масштабе.
На оси абсцисс откладываются как ω, так и lgω.
Десятикратное изменение частоты называется декадой.
Частотой ω для конкретной точки оси абсцисс определяется через lgω → которая имеет равномерный масштаб, также как и L(ω) в отличие от А(ω) имеет равномерный масштаб. диапазоны А(ω) и ω получаются значительными.
Например.  , и аналогично
, и аналогично 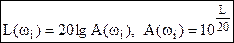 .
.
На оси абсцисс А(ω) = 1, и соответственно L(ω) = 0 дб.
Методика построения ЛАЧХ
Главным достоинством ЛЧХ является возможность построения ЛАЧХ без вычислительной работы в виде кусочно-ломаной прямой, которая называется асимптотической ЛАЧХ. Все отрезки этой ЛАЧХ имеют наклоны, кратные величине ±20 дб/дек.
Для иллюстрации простоты построения ЛАЧХ рассмотрим ряд важных примеров:
1. W(s) = K, А(ω) = K, тогда L(ω) = 20lgK – прямая, параллельная оси ω.
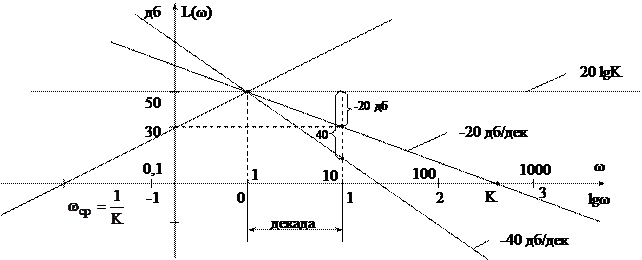 |
2. 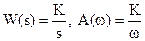 , тогда L(ω) = 20lgK – 20lgω. (20lgK = const, lgω – новая переменная)
, тогда L(ω) = 20lgK – 20lgω. (20lgK = const, lgω – новая переменная)
Из этого уравнения видно, что это прямая с наклоном -20 дб/дек. Координаты (ω = 1, L(ω) = 20lgK) и (L(ω) = 0, ω = K).
Вопрос: Почему наклон -20 дб/дек?
Ответ: при ω = 1, L = 20lgK,
при ω = 10, L = 20lgK – 20,
т.е. частота увеличилась в 10 раз, а спад ЛАЧХ равен 20 дб. Отсюда и терминология – 20 дб/дек.
В принципе такую характеристику проводят через одну опорную точку, а затем находят точку на десятикратно увеличенной частоте. Обычно декада – отрезок в мм (Δlgω = 1).
3. 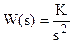 ,
,  , L(ω) = 20 lgK – 40 lgω.
, L(ω) = 20 lgK – 40 lgω.  (из
(из 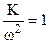 ).
).
Аналогично, это прямая с наклоном – 40 дб/дек.
4. W(s) = Ks, A(ω) = Kω, тогда L(ω) = 20 lgK + 20 lgω.
Аналогично, но наклон + 20 дб/дек.
Частота среза (А(ω) = 1) равна 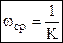 (из А(ω) = Kω = 1).
(из А(ω) = Kω = 1).
Предварительный вывод: Благодаря логарифмической сетке простейшие нелинейные зависимости выпрямляются (растягиваются) в прямую линию.
5.  ,
,  .
.
Отсюда наклон прямой ±20n дб/дек,  .
.
6. 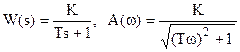 .
. 
при  и L(ω) ≈ 20 lgK;
и L(ω) ≈ 20 lgK;
при 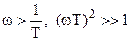 и L(ω) ≈ 20 lgK – 20 lg(Тω)
и L(ω) ≈ 20 lgK – 20 lg(Тω)
Это прямая с наклоном – 20 дб/дек, начиная от точки 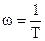 .
.
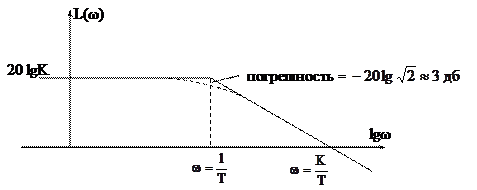

7.  ;
; 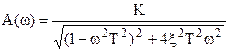 ,
, 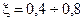 .
.

при 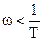 имеем L(ω) = 20 lgK, пренебрегаем
имеем L(ω) = 20 lgK, пренебрегаем  , т.к.
, т.к.
 ;
;
при 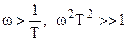 , тогда
, тогда 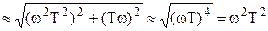 .
.
Поэтому  .
.
Вывод: Начиная с частоты 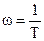 характеристика претерпевает излом на – 40 дб/дек. Если оператор
характеристика претерпевает излом на – 40 дб/дек. Если оператор 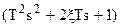 находится в числителе W(s), то наклон будет +40 дб/дек.
находится в числителе W(s), то наклон будет +40 дб/дек.
 |
Погрешность в т. 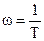 равна:
равна:
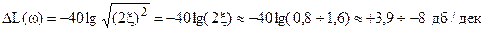 .
.
Оптимальный вариант: при 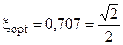 имеем 6 дб/дек.
имеем 6 дб/дек.
| <== предыдущая | | | следующая ==> |
| Вопрос 5. Оценка эффективности инвестиционных проектов | | | Особенности и основные направления внешней политики |
Date: 2015-08-15; view: 321; Нарушение авторских прав
 или
или 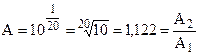 , т.е. небольшая величина.
Вопрос: из акустики – по отношению к чему определяется дБ.
Ответ: порог чувствительности уха – шепот в библиотеке.
, т.е. небольшая величина.
Вопрос: из акустики – по отношению к чему определяется дБ.
Ответ: порог чувствительности уха – шепот в библиотеке.