Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Лекция 12

6.4. Вставка и удаление элементов в АВЛ-дереве   Рассмотрим операцию включения в сбалансированное дерево нового узла. Пусть дан узел 20 с левым и правым поддеревьями L и R. Предположим, что новый узел включается в L, вызывая увеличение его высоты на 1. 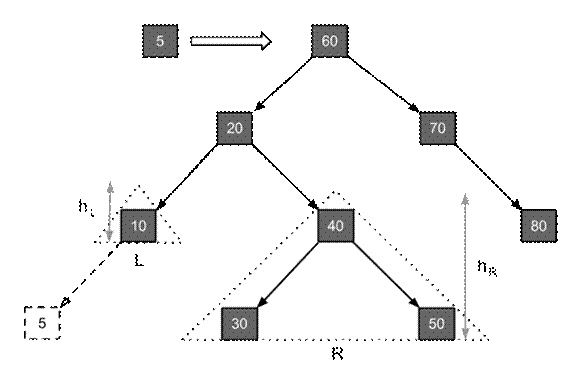Вообще возможны 3 случая после включения:
  1. Если hL = hR до включения, то L и R становятся неравной высоты, но критерий сбалансированности не нарушен.
  2. Если hL < hR до включения, то L и R становятся равной высоты и сбалансированность даже улучшается.
  3. Если hL > hR до включения, то критерий сбалансированности нарушается, и дерево нужно перестраивать.
Повороты узла, разбалансированного вправо, выполняются по симметричной схеме и носят названия однократного L-поворота и двойного RL-поворота. В общих чертах процесс включения узла в сбалансированное дерево состоит из трех этапов:
  1. Поиск места включения узла в каком-либо листе.
  2. Включение нового узла и определение нового показателя сбалансированности в месте включения.
  3. Обратный проход по пути включения и проверка сбалансированности у каждого узла на этом пути.
Математический анализ алгоритма вставки сложен. Эмпирические проверки этого алгоритма показывают, что ожидаемая высота сбалансированного дерева равна h = log2 n + 0,25. То есть АВЛ-деревья ведут себя как идеально сбалансированные полные деревья. Однако, затраты на балансировку АВЛ-дерева значительны. Балансировка необходима приблизительно 1 раз на два включения и однократный и двукратный повороты равновероятны. Из-за сложности операций балансировки АВЛ-деревья рекомендуется использовать в случае, если число операций поиска значительно превышает число операций включения и удаления. При удалении узлов из АВЛ-дерева операция балансировки в основном остается такой же, что и при включении и заключается в однократном или двукратном повороте. При этом булевская переменная h, возвращаемая операцией удаления означает уменьшение высоты поддерева. При восходящем пересчете критерия сбалансированности выполняется балансировка тех узлов, у которых критерий стал равным +2 или -2. Балансировка выполняется с помощью тех же L-, R-, RL- и LR-поворотов.       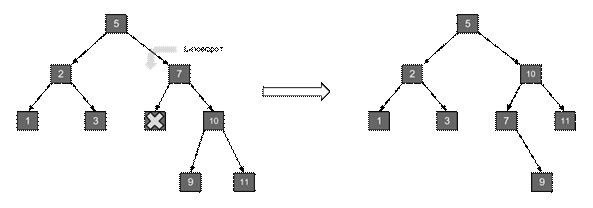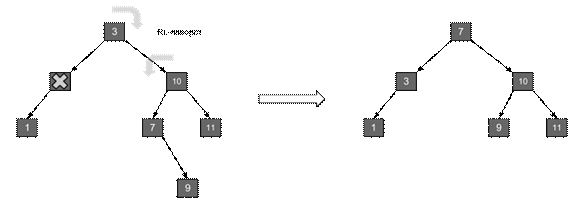Удаление элементов также имеет стоимость О(log2 n). Но если включение может вызвать один поворот, удаление может потребовать повороты в каждом узле пути поиска при обратном ходе рекурсии. Но эмпирические проверки показали, что если при включении выполняется один поворот на каждые два включения, то при удалении один поворот приходится на 5 удалений. 6.5. 2-3-дерево и Б-деревья: вставка и удаление элементов. Применение Б-деревьев для хранения индексов в базах данных   Б-дерево — структура данных, дерево поиска. С точки зрения внешнего логического представления, это сбалансированное, сильно ветвистое дерево во внешней памяти. Использование Б-деревьев впервые было предложено Рудольфом Байером и Эдвардом Маккрейтом в 1970 году. Сбалансированность означает, что длина любых двух путей от корня до листов различается не более, чем на единицу. Ветвистость дерева — это свойство каждого узла дерева ссылаться на некоторое число узлов-потомков.   С точки зрения физической организации Б-дерево представляется как мультисписочная структура страниц внешней памяти, то есть каждому узлу дерева соответствует блок внешней памяти (страница). Внутренние и листовые страницы обычно имеют разную структуру.   Структура Б-дерева применяется для организации индексов во многих современных СУБД. Б-дерево может применяться для структурирования (индексирования) информации на жестком диске (как правило, метаданных). Время доступа к произвольному блоку на жестком диске очень велико (порядка миллисекунд), поскольку оно определяется скоростью вращения диска и перемещения головок. Поэтому важно уменьшить количество узлов, просматриваемых при каждой операции. Использование поиска по списку каждый раз для нахождения случайного блока могло бы привести к чрезмерному количеству обращений к диску, вследствие необходимости осуществления последовательного прохода по всем его элементам, предшествующим заданному; тогда как поиск в Б-дереве, благодаря свойствам сбалансированности и высокой ветвистости, позволяет значительно сократить количество таких операций.   2-3-дерево является идеально сбалансированным деревом поиска. Все пути от корня до любого листа имеют одинаковую длину. Свойства структуры 2-3-дерева следующие:
  • узлы дерева делятся на два вида — внутренние и листья;
  • элементы множества располагаются только в листьях дерева в линейном возрастающем порядке;
  • внутренний узел имеет два или три сына.
В каждый внутренний узел записывается ключ наименьшего элемента, являющегося потомком второго сына и ключ наименьшего элемента – потомка третьего сына, если третий сын есть.   2-3-дерево соответствует полному, идеально сбалансированному BST-дереву, если все его узлы являются 2-узлами. В этом случае его высота равна log2 n. С другой стороны, если все узлы в 2-3-дереве – 3-узлы, то высота 2-3-дерева равна log3 n. Таким образом, длина прохода от корня дерева к листьям с элементами и, следовательно, трудоемкость операций лежит в пределах O(log3 n)-O(log2 n). Поиск элемента в 2-3-дереве:   Элемент можно найти за время O(log2 n), сравнивая ключ искомого элемента с параметрами в узлах. Если ключ меньше, чем минимальный элемент у второго сына, то выбирается первый сын. Иначе, если узел имеет двух сыновей, выбирается второй сын. Если есть третий сын, то выбирается второй сын, если ключ меньше минимального ключа третьего сына, или третий сын в противном случае. Таким образом, поиск приводит к листу с искомым ключом. 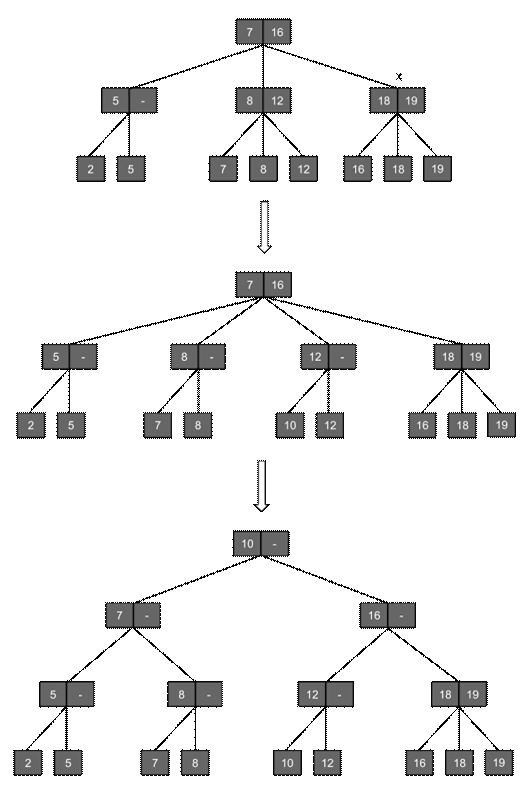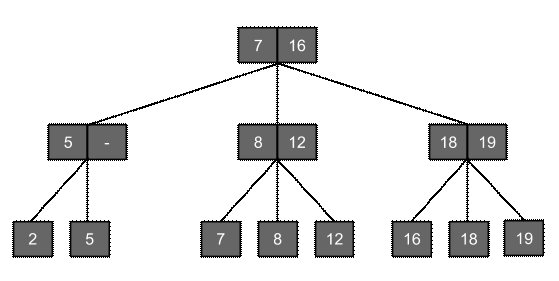Включение элемента в 2-3-дерево:   Включение нового элемента начинается также как и процесс поиска. Пусть мы находимся в некотором внутреннем узле х, чьи сыновья не содержат элемента с заданным ключом k. Если узел содержит двух сыновей, то новый элемент подключается к этому узлу в качестве третьего сына. Новый элемент помещается так, чтобы не нарушить упорядоченность сыновей. После этого корректируются значения минимальных ключей в узле. Например, включаем элемент с ключом 18. При поиске мы приходим к самому правому внутреннему узлу x. Помещаем 18 среди сыновей этого узла в порядке 16, 18, 19. В узле x записываются копии ключей 18 и 19. Если при подключении к узлу, новый элемент является четвертым, то узел х расщепляется на 2 узла x и x'. Два наименьших элемента переносятся в узел х, а два наибольших – в x'. Теперь надо вставить узел x' среди сыновей родителя х. Здесь ситуация повторяется. Если родитель имеет двух сыновей, то узел x' становится третьим сыном. Если родитель имеет трех сыновей, то он в свою очередь расщепляется на два узла. Процесс восходящего расщепления идет в случае необходимости выше и может достигнуть корня дерева. При необходимости расщепления корня создается новый корень, сыновьями которого становятся два узла, получившиеся при разбиении старого корня. Пусть мы вставляем элемент с ключом 10. Выбранный внутренний узел до подключения имеет трех сыновей, поэтому он разбивается на два узла. В свою очередь корень теперь имеет 4 сына и также разбивается на два узла. При этом создается новый корень, объединяющий два узла, получившихся после разбиения старого корня. 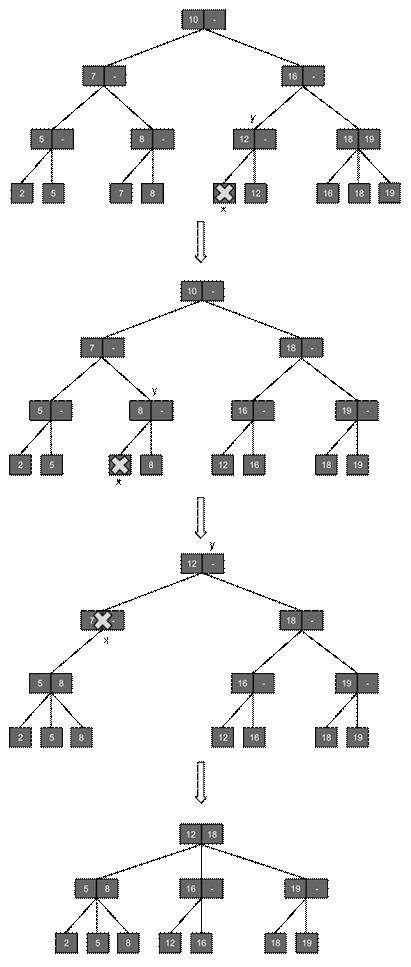Удаление элемента из 2-3-дерева:   Если при удалении узла x у родителя у останется один сын и узел у является корнем, то родитель удаляется из дерева, а корнем становится его единственный сын. Пусть родитель не является корнем. Тогда, если братья узла у имеют трех сыновей, то один из этих сыновей передаются узлу у, и у него становится двое сыновей. Если братья имеют двух сыновей, то единственный сын узла у передается одному из братьев в качестве третьего сына. Узел у после этого удаляется. Если после этого у родителя удаленного узла у останется один сын, то процесс перестройки повторяется для него.

 

<== предыдущая | следующая ==>
Лекция 11: Точность систем автоматического управления | Лекция 12: Показатели качества динамических свойств систем управления

Date: 2015-08-15; view: 381; Нарушение авторских прав; Помощь в написании работы --> СЮДА...


mydocx.ru - 2015-2024 year. (0.006 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию