Принцип освобождаемости от связей

Связь можно отбросить, заменив действие связи силой реакции связи.

.

Здесь к активным силам, равнодействующая которых F, добавляется динамическая реакция связи R. Реакция R является пассивной силой, так как зависит от приложенных к точке активных сил, физических свойств связи и движения точки. Последнее определяет ее отличие от реакции связи в статике, что подчеркивается ее названием.

Реакцию связи R можно всегда разложить по двум направлениям на составляющие, одну из которых N направить по нормали к поверхности связи, определяемой (1), а другую — в плоскости, перпендикулярной к нормали. Если второй составляющей пренебречь, то поверхность можно считать абсолютно гладкой, а связь — идеальной. В этом случае реакцию связи представляют в виде

,

где λ = N/grad(f) — скалярный коэффициент, называемый множителем Лагранжа (связи). Векторное уравнение движения несвободной точки с идеальной связью принимает вид

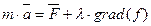(2)

В проекциях на оси декартовой системы координат получаем уравнения

,

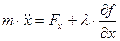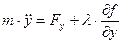, (3)

.

известные как уравнения Лагранжа первого рода.

Три дифференциальных уравнения (3) и уравнение связи (1) содержат четыре неизвестные функции, следовательно, решение возможно. Однако в декартовых координатах при произвольном выборе системы отсчета аналитическое решение задачи удается получить лишь для простейших связей первого порядка.

Date: 2015-08-15; view: 466; Нарушение авторских прав