
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 23 page
|
|
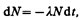 (256.1)
(256.1)
где l — постоянная для данного радиоактивного вещества величина, называемая постоянной радиоактивного распада; знак минус указывает, что общее число радиоактивных ядер в процессе распада уменьшается. Разделив переменные и интегрируя:
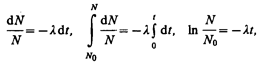
получим
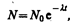 (256.2)
(256.2)
где N 0 — начальное число нераспавшихся ядер (в момент времени t =0), N— число нераспавшихся ядер в момент времени t. Формула (256.2) выражает закон радиоактивного распада, согласно которому число нераспавшихся ядер убывает со временем по экспоненциальному закону.
Интенсивность процесса радиоактивного распада характеризуют две величины: период полураспада Т 1/2 и среднее время жизни t радиоактивного ядра. Период полураспада Т 1/2 — время, за которое исходное число радиоактивных ядер в среднем уменьшается вдвое. Тогда, согласно (256.2),
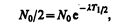
откуда
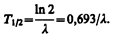
Периоды полураспада для естественно-радиоактивных элементов колеблются от десятимиллионных долей секунды до многих миллиардов лет.
Суммарная продолжительность жизни d N ядер равна t|dN|=lNt d t. Проинтегрировав это выражение по всем возможным t (т. е. от 0 до ¥) и разделив на начальное число ядер N 0, получим среднее время жизни t радиоактивного ядра:
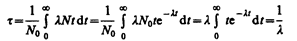
(учтено (256.2)). Таким образом, среднее время жизни t радиоактивного ядра есть величина, обратная постоянной радиоактивного распада l.
Активностью А нуклида (общее название атомных ядер, отличающихся числом протонов Z и нейтронов N) в радиоактивном источнике называется число распадов, происходящих с ядрами образца в 1 с:
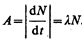 (256.3)
(256.3)
Единица активности в СИ — беккерель (Бк): 1 Бк — активность нуклида, при которой за 1 с происходит один акт распада. До сих пор в ядерной физике применяется и внесистемная единица активности нуклида в радиоактивном источнике — кюри (Ки): 1 Ки= 3,7×1010Бк.
Радиоактивный распад происходит в соответствии с так называемыми правилами смещения, позволяющими установить, какое ядро возникает в результате распада данного материнского ядра. Правила смещения:
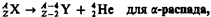 (256.4)
(256.4)
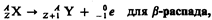 (256.5)
(256.5)
где 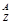 Х — материнское ядро, Y — символ дочернего ядра,
Х — материнское ядро, Y — символ дочернего ядра, 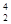 Не — ядро гелия (a -частица),
Не — ядро гелия (a -частица), 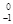 е— символическое обозначение электрона (заряд его равен –1, а массовое число — нулю). Правила смещения являются ничем иным, как следствием двух законов, выполняющихся при радиоактивных распадах, — сохранения электрического заряда и сохранения массового числа: сумма зарядов (массовых чисел) возникающих ядер и частиц равна заряду (массовому числу) исходного ядра.
е— символическое обозначение электрона (заряд его равен –1, а массовое число — нулю). Правила смещения являются ничем иным, как следствием двух законов, выполняющихся при радиоактивных распадах, — сохранения электрического заряда и сохранения массового числа: сумма зарядов (массовых чисел) возникающих ядер и частиц равна заряду (массовому числу) исходного ядра.
Возникающие в результате радиоактивного распада ядра могут быть, в свою очередь, радиоактивными. Это приводит к возникновению цепочки, или ряда, радиоактивных превращений, заканчивающихся стабильным элементом. Совокупность элементов, образующих такую цепочку, называется радиоактивным семейством.

Из правил смещения (256.4) и (256.5) вытекает, что массовое число при a -распаде уменьшается на 4, а при b -распаде не меняется. Поэтому для всех ядер одного и того же радиоактивного семейства остаток от деления массового числа на 4 одинаков. Таким образом, существует четыре различных радиоактивных семейства, для каждого из которых массовые числа задаются одной из следующих формул:
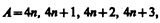
где n — целое положительное число. Семейства называются по наиболее долгоживущему (с наибольшим периодом полураспада) «родоначальнику»: семейства тория (от 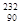 Th), нептуния (от
Th), нептуния (от 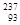 Np), урана (от
Np), урана (от 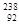 U) и актиния (от
U) и актиния (от  Ас). Конечными нуклидами соответственно являются
Ас). Конечными нуклидами соответственно являются 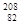 Pb,
Pb, 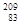 Bi,
Bi, 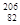 Pb,
Pb, 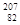 Pb, т.е. единственное семейство нептуния (искусственно-радиоактивные ядра) заканчивается нуклидом Bi, а все остальные (естественно-радиоактивные ядра) — нуклидами Рb.
Pb, т.е. единственное семейство нептуния (искусственно-радиоактивные ядра) заканчивается нуклидом Bi, а все остальные (естественно-радиоактивные ядра) — нуклидами Рb.
§ 257. Закономерности a-распада
В настоящее время известно более двухсот a -активных ядер, главным образом тяжелых (А> 200, Z >82). Только небольшая группа a -активных ядер приходится на область с А = 140 ¸160 (редкие земли). a -Распад подчиняется правилу смещения (256.4). Примером a -распада служит распад изотопа урана 238U с образованием Th:
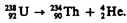
Скорости вылетающих при распаде a --частиц очень велики и колеблются для разных ядер в пределах от 1,4×107 до 2×107 м/с, что соответствует энергиям от 4 до 8,8 МэВ. Согласно современным представлениям, a -частицы образуются в момент радиоактивного распада при встрече движущихся внутри ядра двух протонов и двух нейтронов.
a -Частицы, испускаемые конкретным ядром, обладают, как правило, определенной энергией. Более тонкие измерения, однако, показали, что энергетический спектр a -частиц, испускаемых данным радиоактивным элементом, обнаруживает «тонкую структуру», т. е. испускается несколько групп a -частиц, причем в пределах каждой группы их энергии практически постоянны. Дискретный спектр a -частиц свидетельствует о том, что атомные ядра обладают дискретными энергетическими уровнями.
Для a -распада характерна сильная зависимость между периодом полураспада T 1/2 и энергией Е вылетающих частиц. Эта взаимосвязь определяется эмпирическим законом Гейгера — Нэттола (1912)*, который обычно выражают в виде зависимости между пробегом Ra (расстоянием, проходимым частицей в веществе до ее полной остановки) a -частиц в воздухе и постоянной радиоактивного распада l:
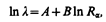 (257.1)
(257.1)
где А и В— эмпирические константы, l = (ln 2)/ T 1/2. Согласно (257.1), чем меньше период полураспада радиоактивного элемента, тем больше пробег, а следовательно, и энергия испускаемых им a -частиц. Пробег a -частиц в воздухе (при нормальных условиях) составляет несколько сантиметров, в более плотных средах он гораздо меньше, составляя сотые доли миллиметра (a -частицы можно задержать обычным листом бумаги).
* Д. Нэттол (1890—1958) — английский физик; X. Гейгер (1882—1945) — немецкий физик.
Опыты Резерфорда по рассеянию a -частиц на ядрах урана показали, что a -частицы вплоть до энергии 8,8 МэВ испытывают на ядрах резерфордовское рассеяние, т. е. силы, действующие на a -частицы со стороны ядер, описываются законом Кулона. Подобный характер рассеяния a -частиц указывает на то, что они еще не вступают в область действия ядерных сил, т. е. можно сделать вывод, что ядро окружено потенциальным барьером, высота которого не меньше 8,8 МэВ. С другой стороны, a -частицы, испускаемые ураном, имеют энергию 4,2 МэВ. Следовательно, a -частицы вылетают из a -радиоактивного ядра с энергией, заметно меньшей высоты потенциального барьера. Классическая механика этот результат объяснить не могла.
Объяснение a -распада дано квантовой механикой, согласно которой вылет a -частицы из ядра возможен благодаря туннельному эффекту (см. § 221) — проникновению a -частицы сквозь потенциальный барьер. Всегда имеется отличная от нуля вероятность того, что частица с энергией, меньшей высоты потенциального барьера, пройдет сквозь вето, т. е., действительно, из a -радиоактивного ядра a -частицы могут вылетать с энергией, меньшей высоты потенциального барьера. Этот эффект целиком обусловлен волновой природой a -частиц.
Вероятность прохождения a -частицы сквозь потенциальный барьер определяется его формой и вычисляется на основе уравнения Шредингера. В простейшем случае потенциального барьера с прямоугольными вертикальными стенками (см. рис. 298, а) коэффициент прозрачности, определяющий вероятность прохождения сквозь него, определяется рассмотренной ранее формулой (221.7):
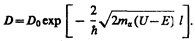
Анализируя это выражение, видим, что коэффициент прозрачности D тем больше (следовательно, тем меньше период полураспада), чем меньший по высоте (U) и ширине (l) барьер находится на пути a -частицы. Кроме того, при одной и той же потенциальной кривой барьер на пути частицы тем меньше, чем больше ее энергия Е. Таким образом качественно подтверждается закон Гейгера — Нэттола (см. (257.1)).
§ 258. b –-Распад. Нейтрино
Явление b –-распада (в дальнейшем будет показано, что существует и b +-распад) подчиняется правилу смещения (256.5)
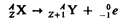
и связано с выбросом электрона. Пришлось преодолеть целый ряд трудностей с трактовкой b –-распада.
Во-первых, необходимо было обосновать происхождение электронов, выбрасываемых в процессе b –-распада. Протонно-нейтронное строение ядра исключает возможность вылета электрона из ядра, поскольку в ядре электронов нет. Предположение же, что электроны вылетают не из ядра, а из электронной оболочки, несостоятельно, поскольку тогда должно было бы наблюдаться оптическое или рентгеновское излучение,что не подтверждают эксперименты.
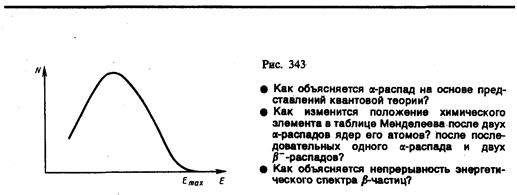
Во-вторых, необходимо было объяснить непрерывность энергетического спектра испускаемых электронов (типичная для всех изотопов кривая распределения b –-частиц по энергиям приведена на рис. 343). Каким же образом b –-активные ядра, обладающие до и после распада вполне определенными энергиями, могут выбрасывать электроны со значениями энергии от нуля до некоторого максимального E mах? Т.е. энергетический спектр испускаемых электронов является непрерывным? Гипотеза о том, что при b –-распаде электроны покидают ядро со строго определенными энергиями, но в результате каких-то вторичных взаимодействий теряют ту или иную долю своей энергии, так что их первоначальный дискретный спектр превращается в непрерывный, была опровергнута прямыми калориметрическими опытами. Так как максимальная энергия E mах определяется разностью масс материнского и дочернего ядер, то распады, при которых энергия электрона Е< E mах,как бы протекают с нарушением закона сохранения энергии. Н. Бор даже пытался обосновать это нарушение, высказывая предположение, что закон сохранения энергии носит статистический характер и выполняется лишь в среднем для большого числа элементарных процессов. Отсюда видно, насколько принципиально важно было разрешить это затруднение.
В-третьих, необходимо было разобраться с несохранением спина при b –-распаде. При b –-распаде число нуклонов в ядре не изменяется (так как не изменяется массовое число А), поэтому не должен изменяться и спин ядра, который равен целому числу 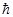 при четном А и полуцелому
при четном А и полуцелому 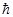 при нечетном А. Однако выброс электрона, имеющего спин
при нечетном А. Однако выброс электрона, имеющего спин 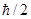 , должен изменить спин ядра на величину
, должен изменить спин ядра на величину 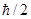 .
.
Последние два затруднения привели В. Паули к гипотезе (1931) о том, что при b –-распаде вместе с электроном испускается еще одна нейтральная частица — нейтрино. Нейтрино имеет нулевой заряд, спин 1/2 (в единицах 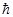 ) и нулевую (а скорее <10–4 тe) массу покоя; обозначается
) и нулевую (а скорее <10–4 тe) массу покоя; обозначается 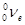 . Впоследствии оказалось, что при b –-распаде испускается не нейтрино, а антинейтрино (античастица по отношению к нейтрино; обозначается
. Впоследствии оказалось, что при b –-распаде испускается не нейтрино, а антинейтрино (античастица по отношению к нейтрино; обозначается 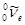 ).
).
Гипотеза о существовании нейтрино позволила Э. Ферми создать теорию b –-распада (1934), которая в основном сохранила свое значение и в настоящее время, хотя экспериментально существование нейтрино было доказано более чем через 20 лет (1956). Столь длительные «поиски» нейтрино сопряжены с большими трудностями, обусловленными отсутствием у нейтрино электрического заряда и массы. Нейтрино — единственная частица, не участвующая ни в сильных, ни в электромагнитных взаимодействиях; единственный вид взаимодействий, в котором может принимать участие нейтрино, — слабое взаимодействие. Поэтому прямое наблюдение нейтрино весьма затруднительно. Ионизирующая способность нейтрино столь мала, что один акт ионизации в воздухе приходится на 500 км пути. Проникающая же способность нейтрино столь огромна (пробег нейтрино с энергией 1 МэВ в свинце составляет примерно 1018 м!), что затрудняет удержание этих частиц в приборах.
Для экспериментального выявления нейтрино (антинейтрино) применялся поэтому косвенный метод, основанный на том, что в реакциях (в том числе и с участием нейтрино) выполняется закон сохранения импульса. Таким образом, нейтрино было обнаружено при изучении отдачи атомных ядер при b –-распаде. Если при b –-распаде ядра вместе с электроном выбрасывается и антинейтрино, то векторная сумма трех импульсов — ядра отдачи, электрона и антинейтрино — должна быть равна нулю. Это действительно подтвердилось на опыте. Непосредственное обнаружение нейтрино стало возможным лишь значительно позднее, после появления мощных реакторов, позволяющих получать интенсивные потоки нейтрино.
Введение нейтрино (антинейтрино) позволило не только объяснить кажущееся несохранение спина, но и разобраться с вопросом непрерывности энергетического спектра выбрасываемых электронов. Сплошной спектр b –-частиц обусловлен распределением энергии между электронами и антинейтрино, причем сумма энергий обеих частиц равна Е max. В одних актах распада большую энергию получает антинейтрино, в других — электрон; в граничной точке кривой на рис. 343, где энергия электрона равна Е max, вся энергия распада уносится электроном, а энергия антинейтрино равна нулю.
Наконец, рассмотрим вопрос о происхождении электронов при b –-распаде. Поскольку электрон не вылетает из ядра и не вырывается из оболочки атома, было сделано предположение, что b - электрон рождается в результате процессов, происходящих внутри ядра. Так как при b –-распаде число нуклонов в ядре не изменяется, a Z увеличивается на единицу (см. (265.5)), то единственной возможностью одновременного осуществления этих условий является превращение одного из нейтронов b –-активного ядра в протон с одновременным образованием электрона и вылетом антинейтрино:
 (258.1)
(258.1)
В этом процессе выполняются законы сохранения электрических зарядов, импульса и массовых чисел. Кроме того, данное превращение энергетически возможно, так как масса покоя нейтрона превышает массу атома водорода, т. е. протона и электрона вместе взятых. Данной разности в массах соответствует энергия, равная 0,782 МэВ. За счет этой энергии может происходить самопроизвольное превращение нейтрона в протон; энергия распределяется между электроном и антинейтрино.
Если превращение нейтрона в протон энергетически выгодно и вообще возможно, то должен наблюдаться радиоактивный распад свободных нейтронов (т. е. нейтронов вне ядра). Обнаружение этого явления было бы подтверждением изложенной теории b –-распада. Действительно, в 1950 г. в потоках нейтронов большой интенсивности, возникающих в ядерных реакторах, был обнаружен радиоактивный распад свободных нейтронов, происходящий по схеме (258.1). Энергетический спектр возникающих при этом электронов соответствовал приведенному на рис. 343, а верхняя граница энергии электронов E max оказалась равной рассчитанной выше (0,782 МэВ).
§ 259. Гамма-излучение и его свойства
Экспериментально установлено, что g -излучение (см. § 255) не является самостоятельным видом радиоактивности, а только сопровождает a - и b -распады и также возникает при ядерных реакциях, при торможении заряженных частиц, их распаде и т. д. g -Спектр является линейчатым. g -Спектр — это распределение числа g -квантов по энергиям (такое же толкование b -спектра дано в §258). Дискретность g -спектра имеет принципиальное значение, так как является доказательством дискретности энергетических состояний атомных ядер.
В настоящее время твердо установлено, что g -излучение испускается дочерним (а не материнским) ядром. Дочернее ядро в момент своего образования, оказываясь возбужденным, за время примерно 10–13—10–14 с, значительно меньшее времени жизни возбужденного атома (примерно 10–8 с), переходит в основное состояние с испусканием g -излучения. Возвращаясь в основное состояние, возбужденное ядро может пройти через ряд промежуточных состояний, поэтому g -излучение одного и того же радиоактивного изотопа может содержать несколько групп g -квантов, отличающихся одна от другой своей энергией.
При g -излучении А и Z ядра не изменяются, поэтому оно не описывается никакими правилами смещения. g -Излучение большинства ядер является столь коротковолновым, что его волновые свойства проявляются весьма слабо. Здесь на первый план выступают корпускулярные свойства, поэтому g -излучение рассматривают как поток частиц — g -квантов. При радиоактивных распадах различных ядер g -кванты имеют энергии от 10 кэВ до 5 МэВ.
Ядро, находящееся в возбужденном состоянии, может перейти в основное состояние не только при испускании g -кванта, но и при непосредственной передаче энергии возбуждения (без предварительного испускания g -кванта) одному из электронов того же атома. При этом испускается так называемый электрон конверсии. Само явление называется внутренней конверсией. Внутренняя конверсия — процесс, конкурирующий с g -излучением.
Электронам конверсии соответствуют дискретные значения энергии, зависящей от работы выхода электрона из оболочки, из которой электрон вырывается, и от энергии Е, отдаваемой ядром при переходе из возбужденного состояния в основное. Если вся энергия Е выделяется в виде g -кванта, то частота излучения n определяется из известного соотношения E=hn. Если же испускаются электроны внутренней конверсии, то их энергии равны Е—АK, E—AL,.... где AK, AL,... — работа выхода электрона из К- и L -оболочек. Моноэнергетичность электронов конверсии позволяет отличить их от b -электронов, спектр которых непрерывен (см. § 258). Возникшее в результате вылета электрона вакантное место на внутренней оболочке атома будет заполняться электронами с вышележащих оболочек. Поэтому внутренняя конверсия всегда сопровождается характеристическим рентгеновским излучением.
g -Кванты, обладая нулевой массой покоя, не могут замедляться в среде, поэтому при прохождении g -излучения сквозь вещество они либо поглощаются, либо рассеиваются им. g -Кванты не несут электрического заряда и тем самым не испытывают влияния кулоновских сил. При прохождении пучка g -квантов сквозь вещество их энергия не меняется, но в результате столкновений ослабляется интенсивность, изменение которой описывается экспоненциальным законом I = I 0e– mx (I 0 и I — интенсивности g -излучения на входе и выходе слоя поглощающего вещества толщиной х, m — коэффициент поглощения). Так как g -излучение — самое проникающее излучение, то m для многих веществ — очень малая величина; m зависит от свойств вещества и от энергии g -квантов.
g -Кванты, проходя сквозь вещество, могут взаимодействовать как с электронной оболочкой атомов вещества, так и с их ядрами. В квантовой электродинамике доказывается, что основными процессами, сопровождающими прохождение g -излучения через вещество, являются фотоэффект, комптон-эффект (комптоновское рассеяние) и образование электронно-позитронных пар.
Фотоэффект, или фотоэлектрическое поглощение g -излучения, — это процесс, при котором атом поглощает g -квант и испускает электрон. Так как электрон выбивается из одной из внутренних оболочек атома, то освободившееся место заполняется электронами из вышележащих оболочек, и фотоэффект сопровождается характеристическим рентгеновским излучением. Фотоэффект является преобладающим механизмом поглощения в области малых энергий g -квантов (Eg £ 100 кэВ). Фотоэффект может идти только на связанных электронах, так как свободный электрон не может поглотить g -квант, при этом одновременно не удовлетворяются законы сохранения энергии и импульса.
По мере увеличения энергии g -квантов (Eg»0,5 МэВ) вероятность фотоэффекта очень мала и основным механизмом взаимодействия g -квантов с веществом является комптоновское рассеяние (см. § 206).
При Eg >l,02 МэВ=2 meс 2 (тe— масса покоя электрона) становится возможным процесс образования электронно-позитронных пар в электрических полях ядер. Вероятность этого процесса пропорциональна Z 2 и увеличивается с ростом Eg. Поэтому при Eg»10 МэВ основным процессом взаимодействия g -излучения в любом веществе является образованно электронно-позитронных пар.
Если энергия g -кванта превышает энергию связи нуклонов в ядре (7—8 МэВ), то в результате поглощения g -кванта может наблюдаться ядерный фотоэффект — выброс из ядра одного из нуклонов, чаще всего нейтрона.
Большая проникающая способность g -излучения используется в гамма-дефектоскопии — методе дефектоскопии, основанном на различном поглощении g -излучения при распространении его на одинаковое расстояние в разных средах. Местоположение и размеры дефектов (раковины, трещины и т. д.) определяются по различию в интенсивностях излучения, прошедшего через разные участки просвечиваемого изделия.
Воздействие g -излучения (а также других видов ионизирующего излучения) на вещество характеризуют дозой ионизирующего излучения. Различаются:
Поглощенная доза излучения — физическая величина, равная отношению энергии излучения к массе облучаемого вещества.
Единица поглощенной дозы излучения — грей (Гр)*: 1 Гр= 1 Дж/кг — доза излучения, при которой облученному веществу массой 1 кг передается энергия любого ионизирующего излучения 1 Дж.
* С. Грей (1666—1736) — английский физик.
Экспозиционная доза излучения — физическая величина, равная отношению суммы электрических зарядоввсех ионов одного знака, созданных электронами, освобожденными в облученном воздухе (при условии полного использования ионизирующей способности электронов), к массе этого воздуха.
Единица экспозиционной дозы излучения — кулон на килограмм (Кл/кг); внесистемной единицей является рентген (Р): 1 Р=2,58×10–4 Кл/кг.
Биологическая доза — величина, определяющая воздействие излучения на организм.
Единица биологической дозы — биологический эквивалент рентгена (бэр): 1 бэр — доза любого вида ионизирующего излучения, производящая такое же биологическое действие,как и доза рентгеновского или g -излучения в 1 Р (1 бэр = 10–2 Дж/кг).
Мощность дозы излучения — величина, равная отношению дозы излучения к времениоблучения. Различают: 1) мощность поглощенной дозы (единица — грей на секунду (Гр/с)); 2) мощность экспозиционной дозы (единица — ампер на килограмм (А/кг)).
§ 260. Резонансное поглощение g -излучения (эффект Мёссбауэра*)
Как уже указывалось, дискретный спектр g -излучения обусловлен дискретностью энергетических уровней ядер атомов. Однако, как следует из соотношения неопределенностей (215.5), энергия возбужденных состояний ядра принимает значения в пределах D E» h/ D t, где D t — время жизни ядра в возбужденном состоянии. Следовательно, чем меньше D t, тем больше неопределенность энергии D E возбужденного состояния. D E =0 только для основного состояния стабильного ядра (для него D t ®¥). Неопределенность энергии квантово-механической системы (например, атома), обладающей дискретными уровнями энергии, определяет естественную ширину энергетического уровня (Г). Например, при времени жизни возбужденного состояния, равного 10–13 с, естественная ширина энергетического уровня примерно 10–2 эВ.
* Р. Мёссбауэр (р. 1929) — немецкий физик.
Неопределенность энергии возбужденного состояния, обусловливаемая конечным временем жизни возбужденных состоянии ядра, приводит к немонохроматичности g -излучения, испускаемого при переходе ядра из возбужденного состояния в основное. Эта немонохроматичность называется естественной шириной линии g -излучения.
При прохождении g -излучения в веществе помимо описанных выше (см. § 259) процессов (фотоэффект, комптоновское рассеяние, образование электронно-позитронных пар) должны в принципе наблюдаться также резонансные эффекты. Если ядро облучить g -квантами с энергией, равной разности одного из возбужденных и основного энергетических состояний ядра, то может иметь место резонансное поглощение g -излучения ядрами: ядро поглощает g -квант той же частоты, что и частота излучаемого ядром g -кванта при переходе ядра из данного возбужденного состояния в основное.
Наблюдение резонансного поглощения g -квантов ядрами считалось долгое время невозможным, так как при переходе ядра из возбужденного состояния с энергией Е в основное (его энергия принята равной нулю) излучаемый g -квант имеет энергию Еg несколько меньшую,чем Е, из-за отдачи ядра в процессе излучения:
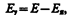
где Е я — кинетическая энергия отдачи ядра. При возбуждении же ядра и переходе его из основного состояния в возбужденное с энергией Е g -квант должен иметь энергию
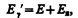
где Е я — энергия отдачи, которую g -квант должен передать поглощающему ядру.
Таким образом, максимумы линий излучения и поглощения сдвинуты друг относительно друга на величину 2 Е я (рис. 344). Используя закон сохранения импульса, согласно которому в рассмотренных процессах излучения и поглощения импульсы g -кванта и ядра должны быть равны, получим
Date: 2015-08-15; view: 424; Нарушение авторских прав